A convex polytope is a special case of a polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

, having the additional property that it is also a convex set

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 of points in the n-dimensional space Rⁿ. Some authors use the terms "convex polytope" and "convex polyhedron" interchangeably, while others prefer to draw a distinction between the notions of a polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 and a polytope.

In addition, some texts require a polytope to be a bounded set

Bounded set

In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...

, while others (including this article) allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts treat a convex n-polytope as a surface or (n-1)-manifold.

Convex polytopes play an important role both in various branches of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 and in applied areas, most notably in linear programming

Linear programming

Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...

.

A comprehensive and influential book in the subject, called Convex Polytopes, was published in 1967 by Branko Grünbaum

Branko Grünbaum

Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....

. In 2003 the 2nd edition of the book was published, with significant additional material contributed by new writers.

In Grünbaum's book, and in some other texts in discrete geometry

Discrete geometry

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...

, convex polytopes are often simply called "polytopes". Grünbaum points out that this is solely to avoid the endless repetition of the word "convex", and that the discussion should throughout be understood as applying only to the convex variety.

A polytope is called full-dimensional, if it is an n-dimensional object in Rⁿ.

Examples

• Many examples of bounded convex polytopes can be found in the article "polyhedron
  Polyhedron
  In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
  
  ".
• In the 2-dimensional case the full-dimensional examples are a half-plane, a strip between two parallel lines, an angle
  Angle
  In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
  
   shape (the intersection of two non-parallel half-planes), a shape defined by a convex polygonal chain
  Polygonal chain
  A polygonal chain, polygonal curve, polygonal path, or piecewise linear curve, is a connected series of line segments. More formally, a polygonal chain P is a curve specified by a sequence of points \scriptstyle called its vertices so that the curve consists of the line segments connecting the...
  
   with two rays attached to its ends, and a convex polygon
  Convex polygon
  In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
  
  .
• Special cases of an unbounded convex polytope are a slab between two parallel hyperplanes, a wedge defined by two non-parallel half-space
  Half-space
  In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
  
  s, a polyhedral cylinder (infinite prism
  Prism (geometry)
  In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
  
  ), and a polyhedral cone (infinite prism
  Prism (geometry)
  In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
  
  ), defined by three or more half-spaces passing through a common point.

Definitions

A convex polytope may be defined in a number of ways, depending on what is more suitable for the problem at hand. Grünbaum's definition is in terms of a convex set of points in space. Other important definitions are: as the intersection

Intersection (set theory)

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

 of half-spaces (half-space representation) and as the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 of a set of points (vertex representation).

Vertex representation (Convex hull)

In his book Convex polytopes, Grünbaum defines a convex polytope as a compact convex set:

A set (where is real space) is convex if, for each pair of distinct points 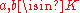, the closed segment with endpoints a and b is contained within K.

A compact convex set 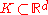is a polytope provided ext K (the set of all extreme point

Extreme point

In mathematics, an extreme point of a convex set S in a real vector space is a point in S which does not lie in any open line segment joining two points of S...

s of K) is a finite set

This is equivalent to defining a finite convex polytope as the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 of a finite set of points, where the finite set must contain the set of extreme points of the polytope. Such a definition is called a vertex representation (V-representation or V-description). There exist infinitely many V-descriptions of a convex polytope. However, for a full-dimensional convex polytope, the minimal V-description is in fact unique and is given by the set of the vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 of the polytope.

Intersection of half-spaces

A convex polytope may be defined as an intersection of a finite number of half-spaces. Such definition is called a half-space representation (H-representation or H-description). There exist infinitely many H-descriptions of a convex polytope. However, for a full-dimensional convex polytope, the minimal H-description is in fact unique and is given by the set of the facet-defining halfspaces.

A closed half-space can be written as a linear inequality

Linear inequality

In mathematics a linear inequality is an inequality which involves a linear function.-Definitions:When two expressions are connected by 'greater than' or 'less than' sign, we get an inequation....

:


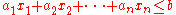
where n is the dimension of the space containing the polytope under consideration. Hence, a closed convex polytope may be regarded as the set of solutions to the system of linear inequalities:


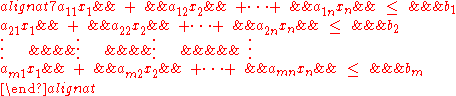
where m is the number of half-spaces defining the polytope. This can be concisely written as the matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

 inequality:


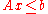
where A is an m×n matrix, x is an n×1 column vector of variables, and b is an m×1 column vector of constants.

An open convex polytope is defined in the same way, with strict inequalities used in the formulas instead of the non-strict ones.

The coefficients of each row of A and b correspond with the coefficients of the linear inequality defining the respective half-space. Hence, each row in the matrix corresponds with a supporting hyperplane of the polytope, a hyperplane bounding a half-space that contains the polytope. If a supporting hyperplane also intersects the polytope, it is called a bounding hyperplane (since it is a supporting hyperplane, it can only intersect the polytope at the polytope's boundary).

The foregoing definition assumes that the polytope is full-dimensional. If it is not, then the solution of Ax ≤ b lies in a proper affine subspace of Rⁿ and discussion of the polytope may be constrained to this subspace.

In general the intersection of arbitrary half-spaces need not be bounded. However if one wishes to have a definition equivalent to that as a convex hull, then bounding must be explicitly required.

Finite basis theorem

The finite basis theorem is an extension of the notion of V-description to include infinite polytopes. The theorem states that a convex polyhedron is the convex sum of its vertices plus the conical sum of the direction vectors of its infinite edges.

Properties

Every (bounded) convex polytope is the image of a simplex

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

, as every point is a convex combination

Convex combination

In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....

 of the (finitely many) vertices. However, polytopes are not in general isomorphic to simplices. This is in contrast to the case of vector spaces and linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

s, every finite dimensional vector space being not only an image of, but in fact isomorphic to, Euclidean space of some dimension (or analog over other fields).

The face lattice

A face

Face (geometry)

In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...

 of a convex polytope is any intersection of the polytope with a halfspace such that none of the interior points of the polytope lie on the boundary of the halfspace. If a polytope is d-dimensional, its facets

Facet (mathematics)

A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...

 are its (d − 1)-dimensional faces, its vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 are its 0-dimensional faces, its edges

Edge (geometry)

In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....

 are its 1-dimensional faces, and its ridges

Ridge (geometry)

In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...

 are its (d − 2)-dimensional faces.

Given a convex polytope P defined by the matrix inequality 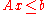, if each row in A corresponds with a bounding hyperplane and is linearly independent of the other rows, then each facet of P corresponds with exactly one row of A, and vice versa. Each point on a given facet will satisfy the linear equality of the corresponding row in the matrix. (It may or may not also satisfy equality in other rows). Similarly, each point on a ridge will satisfy equality in two of the rows of A.

In general, an (n − j)-dimensional face satisfies equality in j specific rows of A. These rows form a basis of the face. Geometrically speaking, this means that the face is the set of points on the polytope that lie in the intersection of j of the polytope's bounding hyperplanes.

The faces of a convex polytope thus form an Eulerian

Eulerian poset

In combinatorial mathematics, an Eulerian poset is a graded poset in which every nontrivial interval has the same number of elements of even rank as of odd rank. An Eulerian poset which is a lattice is an Eulerian lattice. These objects are named after Leonhard Euler...

 lattice

Lattice (order)

In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...

 called its face lattice, where the partial ordering is by set containment of faces. The definition of a face given above allows both the polytope itself and the empty set to be considered as faces, ensuring that every pair of faces has a join and a meet in the face lattice. The whole polytope is the unique maximum element of the lattice, and the empty set, considered to be a (−1)-dimensional face (a null polytope) of every polytope, is the unique minimum element of the lattice.

Two polytopes are called combinatorially isomorphic if their face lattices are isomorphic

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations.  If there exists an isomorphism between two structures, the two structures are said to be isomorphic.  In a certain sense, isomorphic structures are...

.

The polytope graph (polytopal graph, graph of the polytope) is the set of vertices and edges of the polytope only - higher dimensional faces are ignored. For instance, a polyhedral graph

Polyhedral graph

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...

 is the polytope graph of a three-dimensional polytope. By a result of Whitney

Hassler Whitney

Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...

  the face lattice of a three-dimensional polytope is determined by its graph. The same is true if the polytope is simple  (Blind & Mani-Levitska (1987), see Kalai (1988) for a simple proof). The latter fact is instrumental in the proof that from the point of view of computational complexity

Computational Complexity

Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...

, the problem of deciding whether two convex polytopes are combinatorially isomorphic is equivalent to the graph isomorphism problem

Graph isomorphism problem

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.Besides its practical importance, the graph isomorphism problem is a curiosity in computational complexity theory as it is one of a very small number of problems belonging to NP...

, even when restricted to the class of simple or simplicial polytope

Simplicial polytope

In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....

s.

Topological properties

A convex polytope, like any closed convex subset of Rⁿ, is homeomorphic

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

 to a closed ball

Ball (mathematics)

In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....

. Let m denote the dimension of the polytope. If the polytope is full-dimensional, then m = n. The convex polytope therefore is an m-dimensional manifold with boundary, its Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

 is 1, and its fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

 is trivial. The boundary of the convex polytope is homeomorphic to an (m − 1)-sphere. The boundary's Euler characteristic is 0 for even m and 2 for odd m. The boundary may also be regarded as a tessellation

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

 of (m − 1)-dimensional spherical space — i.e. as a spherical tiling.

Simplicial decomposition

A convex polytope can be decomposed into a simplicial complex

Simplicial complex

In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...

, or union of simplices

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

, satisfying certain properties.

Given a convex r-dimensional polytope P, a subset of its vertices containing (r+1) linearly independent points defines an r-simplex

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

. It is possible to form a collection of subsets such that the union of the corresponding simplices is equal to P, and the intersection of any two simplices is either empty or a lower-dimensional simplex.

Construction of representations

Different representations of a convex polytope have different utility, therefore the construction of one representation given another one is an important problem. The problem of the construction of a V-representation is known as the vertex enumeration problem

Vertex enumeration problem

In mathematics, the vertex enumeration problem for a polytope, a polyhedral cell complex, a hyperplane arrangement, or some other object of discrete geometry, is the problem of determination of the object's vertices given some formal representation of the object...

 and the problem of the construction of a H-representation is known as the facet enumeration problem. While the vertex set of a bounded convex polytope uniquely defines it, in various applications it is important to know more about the combinatorial structure of the polytope, i.e., about its face lattice. Various convex hull algorithms

Convex hull algorithms

Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science, see "Convex hull applications"....

 deal both with the facet enumeration and face lattice construction.

In the planar case, i.e., for a convex polygon

Convex polygon

In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...

, both facet and vertex enumeration problems amount to the ordering vertices (resp. edges) around the convex hull. It is a trivial task when the convex polygon is specified in a traditional for polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

s way, i.e., by the ordered sequence of its vertices . When the input list of vertices (or edges) is unordered, the time complexity

Time complexity

In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...

 of the problems becomes O(m log m).

External links

• Komei Fukuda, Polyhedral computation FAQ.