Linear programming
Overview
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
for some list of requirements represented as linear relationships. Linear programming is a specific case of mathematical programming (mathematical optimization).
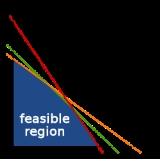
More formally, linear programming is a technique for the optimization of a linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
objective function, subject to linear equality and linear inequality
Linear inequality
In mathematics a linear inequality is an inequality which involves a linear function.-Definitions:When two expressions are connected by 'greater than' or 'less than' sign, we get an inequation....
constraints
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
.
Unanswered Questions

