Cohomological dimension
Encyclopedia
In abstract algebra
, cohomological dimension is an invariant which measures the homological complexity of representations of a group
. It has important applications in geometric group theory
, topology
, and algebraic number theory
.
, R a non-zero ring
with a unit, and RG the group ring
. The group G has cohomological dimension less than or equal to n, denoted cdR(G) ≤ n, if the trivial RG-module R has a projective resolution of length n, i.e. there are projective
RG-modules P0, …, Pn and RG-module homomorphisms dk: Pk
Pk − 1 (k = 1, …, n) and d0: P0
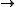R, such that the image of dk coincides with the kernel of dk − 1 for k = 1, …, n and the kernel of dn is trivial.
Equivalently, the cohomological dimension is less than or equal to n if for an arbitrary RG-module M, the cohomology
of G with coeffients in M vanishes in degrees k > n, that is, Hk(G,M) = 0 whenever k > n.
The smallest n such that the cohomological dimension of G is less than or equal to n is the cohomological dimension of G(with coefficients R), which is denoted n = cdR(G).
A free resolution of Z can be obtained from a free action of the group G on a contractible topological space
X. In particular, if X is a contractible CW complex
of dimension n with a free action of a discrete group G that permutes the cells, then cdZ(G) ≤ n.
Now let us consider the case of a general ring R.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, cohomological dimension is an invariant which measures the homological complexity of representations of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. It has important applications in geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, and algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
Cohomological dimension of a group
As most (co)homological invariants, the cohomological dimension involves a choice of a "ring of coefficients" R, with a prominent special case given by R = Z, the ring of integers. Let G be a discrete groupDiscrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
, R a non-zero ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
with a unit, and RG the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
. The group G has cohomological dimension less than or equal to n, denoted cdR(G) ≤ n, if the trivial RG-module R has a projective resolution of length n, i.e. there are projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
RG-modules P0, …, Pn and RG-module homomorphisms dk: Pk
Pk − 1 (k = 1, …, n) and d0: P0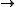R, such that the image of dk coincides with the kernel of dk − 1 for k = 1, …, n and the kernel of dn is trivial.Equivalently, the cohomological dimension is less than or equal to n if for an arbitrary RG-module M, the cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
of G with coeffients in M vanishes in degrees k > n, that is, Hk(G,M) = 0 whenever k > n.
The smallest n such that the cohomological dimension of G is less than or equal to n is the cohomological dimension of G(with coefficients R), which is denoted n = cdR(G).
A free resolution of Z can be obtained from a free action of the group G on a contractible topological space
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
X. In particular, if X is a contractible CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
of dimension n with a free action of a discrete group G that permutes the cells, then cdZ(G) ≤ n.
Examples
In the first group of examples, let the ring R of coefficients be Z.- A free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
has cohomological dimension one. As shown by John Stallings (for finitely generated group) and Richard Swan (in full generality), this property characterizes free groups. - The fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, orientableOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
other than the sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
has cohomological dimension two. - More generally, the fundamental group of a compact, connected, orientable asphericalAspherical spaceIn topology, a branch of mathematics, an aspherical space is a topological space with all higher homotopy groups equal to 0.If one works with CW complexes, one can reformulate this condition: an aspherical CW complex is a CW complex whose universal cover is contractible. Indeed, contractibility of...
manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
n has cohomological dimension n. In particular, the fundamental group of a closed orientable hyperbolic n-manifold has cohomological dimension n. - Nontrivial finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s have infinite cohomological dimension over Z. More generally, the same is true for groups with nontrivial torsion.
Now let us consider the case of a general ring R.
- A group G has cohomological dimension 0 if and only if its group ring RG is semisimpleSemisimple algebraIn ring theory, a semisimple algebra is an associative algebra which has trivial Jacobson radical...
. Thus a finite group has cohomological dimension 0 if and only if its order (or, equivalently, the orders of its elements) is invertible in R. - Generalizing the Stallings–Swan theorem for R = Z, Dunwoody proved that a group has cohomological dimension at most one over an arbitrary ring R if and only if it is the fundamental group of a connected graph of finite groupsGraph of groupsIn geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
whose orders are invertible in R.