Semisimple algebra
Encyclopedia
In ring theory
, a semisimple algebra is an associative algebra
which has trivial Jacobson radical
(only the zero element of the algebra is in the Jacobson radical). If the algebra is finite dimensional this is equivalent to saying that it can be expressed as a Cartesian product of simple subalgebras.
of an algebra over a field is the ideal consisting of all elements that annihilate every simple left-module. The radical contains all nilpotent ideals, and if the algebra is finite-dimensional, the radical itself is a nilpotent ideal. A finite dimensional algebra is then said to be semi-simple if its radical contains only the zero element.
An algebra A is called simple if it has no proper ideals and A2 = {ab | a, b ∈ A} ≠ {0}. As the terminology suggests, simple algebras are semi-simple. Only possible ideals in a simple algebra are A and {0}. Thus if A is not nilpotent, then A is semisimple. Because A2 is an ideal of A and A is simple, A2 = A. By induction, An = A for every positive integer n, i.e. A is not nilpotent.
Any self-adjoint subalgebra A of n × n matrices with complex entries is semisimple. Let Rad(A) be the radical of A. Suppose a matrix M is in Rad(A). Then M*M lies in some nilpotent ideals of A, therefore (M*M)k = 0 for some positive integer k. By positive-semidefiniteness of M*M, this implies M*M = 0. So M x is the zero vector for all x, i.e. M = 0.
If {Ai} is a finite collection of simple algebras, then their Cartesian product ∏ Ai is semi-simple. If (ai) is an element of Rad(A). Let e1 be the multiplicative identity in A1 (all simple algebras possess a multiplicative identity). Then (a1, a2, ...) · (e1, 0, ...) = (a1, 0..., 0) lies in some nilpotent ideal of ∏ Ai. This implies, for all b in A1, a1b is nilpotent in A1, i.e. a1 ∈ Rad(A1). So a1 = 0. Similarly, ai = 0 for all other i.
It is less apparent from the definition that the converse of the above is also true, that is, any finite dimensional semisimple algebra is isomorphic to a Cartesian product of a finite number of simple algebras. The following is a semisimple algebra that appears not to be of this form. Let A be an algebra with Rad(A) ≠ A. The quotient algebra B = A ⁄ Rad(A) is semisimple: If J is a nonzero nilpotent ideal in B, then its preimage under the natural projection map is a nilpotent ideal in A which is strictly larger than Rad(A), a contradiction.
be a composition series
of A, then A is isomorphic to the following Cartesian product:
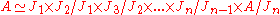
where each
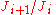
is a simple algebra.
The proof can be sketched as follows. First, invoking the assumption that A is semisimple, one can show that the J1 is a simple algebra (therefore unital). So J1 is a unital subalgebra and an ideal of J2. Therefore one can decompose
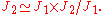
By maximality of J1 as an ideal in J2 and also the semisimplicity of A, the algebra
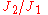
is simple. Proceed by induction in similar fashion proves the claim. For example, J3 is the Cartesian product of simple algebras
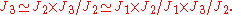
The above result can be restated in a different way. For a semisimple algebra A = A1 ×...× An expressed in terms of its simple factors, consider the units ei ∈ Ai. The elements Ei = (0,...,ei,...,0) are idempotents in A and they lie in the center of A. Furthermore, Ei A = Ai, EiEj = 0 for i ≠ j, and Σ Ei = 1, the multiplicative identity in A.
Therefore, for every semisimple algebra A, there exists idempotents {Ei} in the center of A, such that
completely classifies semisimple algebras: they are isomorphic to a product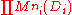
where the 
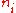are some integers, the 
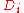are division ring
s, and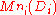
means the ring of 
matrices over 
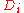. This product is unique up to permutation of the factors.
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, a semisimple algebra is an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
which has trivial Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
(only the zero element of the algebra is in the Jacobson radical). If the algebra is finite dimensional this is equivalent to saying that it can be expressed as a Cartesian product of simple subalgebras.
Definition
The Jacobson radicalJacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of an algebra over a field is the ideal consisting of all elements that annihilate every simple left-module. The radical contains all nilpotent ideals, and if the algebra is finite-dimensional, the radical itself is a nilpotent ideal. A finite dimensional algebra is then said to be semi-simple if its radical contains only the zero element.
An algebra A is called simple if it has no proper ideals and A2 = {ab | a, b ∈ A} ≠ {0}. As the terminology suggests, simple algebras are semi-simple. Only possible ideals in a simple algebra are A and {0}. Thus if A is not nilpotent, then A is semisimple. Because A2 is an ideal of A and A is simple, A2 = A. By induction, An = A for every positive integer n, i.e. A is not nilpotent.
Any self-adjoint subalgebra A of n × n matrices with complex entries is semisimple. Let Rad(A) be the radical of A. Suppose a matrix M is in Rad(A). Then M*M lies in some nilpotent ideals of A, therefore (M*M)k = 0 for some positive integer k. By positive-semidefiniteness of M*M, this implies M*M = 0. So M x is the zero vector for all x, i.e. M = 0.
If {Ai} is a finite collection of simple algebras, then their Cartesian product ∏ Ai is semi-simple. If (ai) is an element of Rad(A). Let e1 be the multiplicative identity in A1 (all simple algebras possess a multiplicative identity). Then (a1, a2, ...) · (e1, 0, ...) = (a1, 0..., 0) lies in some nilpotent ideal of ∏ Ai. This implies, for all b in A1, a1b is nilpotent in A1, i.e. a1 ∈ Rad(A1). So a1 = 0. Similarly, ai = 0 for all other i.
It is less apparent from the definition that the converse of the above is also true, that is, any finite dimensional semisimple algebra is isomorphic to a Cartesian product of a finite number of simple algebras. The following is a semisimple algebra that appears not to be of this form. Let A be an algebra with Rad(A) ≠ A. The quotient algebra B = A ⁄ Rad(A) is semisimple: If J is a nonzero nilpotent ideal in B, then its preimage under the natural projection map is a nilpotent ideal in A which is strictly larger than Rad(A), a contradiction.
Characterization
Let A be a finite dimensional semisimple algebra, andbe a composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
of A, then A is isomorphic to the following Cartesian product:
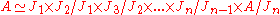
where each
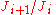
is a simple algebra.
The proof can be sketched as follows. First, invoking the assumption that A is semisimple, one can show that the J1 is a simple algebra (therefore unital). So J1 is a unital subalgebra and an ideal of J2. Therefore one can decompose
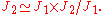
By maximality of J1 as an ideal in J2 and also the semisimplicity of A, the algebra
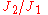
is simple. Proceed by induction in similar fashion proves the claim. For example, J3 is the Cartesian product of simple algebras
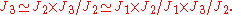
The above result can be restated in a different way. For a semisimple algebra A = A1 ×...× An expressed in terms of its simple factors, consider the units ei ∈ Ai. The elements Ei = (0,...,ei,...,0) are idempotents in A and they lie in the center of A. Furthermore, Ei A = Ai, EiEj = 0 for i ≠ j, and Σ Ei = 1, the multiplicative identity in A.
Therefore, for every semisimple algebra A, there exists idempotents {Ei} in the center of A, such that
- EiEj = 0 for i ≠ j (such a set of idempotents is called orthogonal),
- Σ Ei = 1,
- A is isomorphic to the Cartesian product of simple algebras E1 A ×...× En A.
Classification
The Artin–Wedderburn theoremArtin–Wedderburn theorem
In abstract algebra, the Artin–Wedderburn theorem is a classification theorem for semisimple rings. The theorem states that an Artinian semisimple ring R is isomorphic to a product of finitely many ni-by-ni matrix rings over division rings Di, for some integers ni, both of which are uniquely...
completely classifies semisimple algebras: they are isomorphic to a product
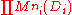where the 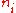are some integers, the 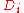are division ringDivision ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s, and
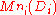means the ring of matrices over 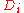. This product is unique up to permutation of the factors.