Classification of manifolds
Encyclopedia
In mathematics
, specifically geometry and topology
, the classification of manifolds is a basic question, about which much is known, and many open questions remain.
s is classifying objects up to isomorphism
.
There are many different notions of "manifold", and corresponding notions of
"map between manifolds", each of which yields a different category
and a different classification question.
These categories are related by forgetful functor
s: for instance, a differentiable manifold is also a topological manifold, and a differentiable map is also continuous, so there is a functor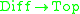
.
These functors are in general neither one-to-one nor onto; these failures are generally referred to in terms of "structure", as follows. A topological manifold that is in the image of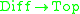
is said to "admit a differentiable structure", and the fiber over a given topological manifold is "the different differentiable structures on the given topological manifold".
Thus given two categories, the two natural questions are:
In more general categories, this structure set has more structure: in Diff it is simply a set, but in Top it is a group, and functorially so.
Many of these structures are G-structure
s, and the question is reduction of the structure group
. The most familiar example is orientability: some manifolds are orientable, some are not, and orientable manifolds admit 2 orientations.
For instance, for orientable surfaces,
the classification of surfaces enumerates them as the connect sum of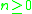
tori, and an invariant that classifies them is the genus
or Euler characteristic
.
Manifolds have a rich set of invariants, including:
Modern algebraic topology (beyond cobordism
theory), such as
Extraordinary (co)homology, is little-used
in the classification of manifolds, because these invariant are homotopy-invariant, and hence don't help with the finer classifications above homotopy type.
Cobordism groups (the bordism groups of a point) are computed, but the bordism groups of a space (such as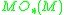
) are generally not.
The most frequently classified class of manifolds is closed, connected manifolds.
Being homogeneous (away from any boundary), manifolds have no local point-set invariants, other than their dimension and boundary versus interior, and the most used global point-set properties are compactness and connectedness. Conventional names for combinations of these are:
For instance,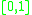
is a compact manifold, 
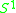is a closed manifold, and 
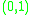is an open manifold, while 
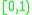is none of these.
invariant, and thus can be effectively computed given a CW structure
, so 2-manifolds are classified homologically.
Characteristic class
es and characteristic numbers are the corresponding generalized homological invariants, but they do not classify manifolds in higher dimension (they are not a complete set of invariants
): for instance, orientable 3-manifolds are parallelizable (Steenrod's theorem in low-dimensional topology
), so all characteristic classes vanish. In higher dimensions, characteristic classes do not in general vanish, and provide useful but not complete data.
Manifolds in dimension 4 and above cannot be effectively classified: given two n-manifolds (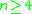
) presented as CW complex
es or handlebodies
, there is no algorithm for determining if they are isomorphic (homeomorphic, diffeomorphic). This is due to the unsolvability of the word problem for groups
, or more precisely, the triviality problem (given a finite presentation for a group, is it the trivial group?). Any finite presentation of a group can be realized as a 2-complex, and can be realized as the 2-skeleton of a 4-manifold (or higher). Thus one cannot even compute the fundamental group
of a given high dimensional manifold, much less a classification.
This ineffectiveness is a fundamental reason why surgery theory does not classify manifolds up to homeomorphism. Instead, for any fixed manifold M it classifies pairs (N,f) with N a manifold and f:N-->M a homotopy equivalence, two such pairs (N,f), (N',f') being regarded as equivalent if there exist a homeomorphism h:N-->N and a homotopy f'h ~ f:N-->M.
. Conversely, negative curvature is generic: for instance, any manifold of dimension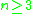
admits a metric with negative Ricci curvature.
This phenomenon is evident already for surfaces: there is a single orientable (and a single non-orientable) closed surface with positive curvature (the sphere and projective plane
),
and likewise for zero curvature (the torus
and the Klein bottle
), and all surfaces of higher genus admit negative curvature metrics only.
Similarly for 3-manifolds: of the 8 geometries
,
all but hyperbolic are quite constrained.
Thus dimension 4 differentiable manifolds are the most complicated:
they are neither geometrizable (as in lower dimension),
nor are they classified by surgery (as in higher dimension or topologically),
and they exhibit unusual phenomena, most strikingly the uncountably infinitely many exotic differentiable structures on R4
. Notably, differentiable 4-manifolds is the only remaining open case of the generalized Poincaré conjecture
.
One can take a low dimensional point of view on high dimensional manifolds
and ask "Which high dimensional manifolds are geometrizable?",
for various notions of geometrizable (cut into geometrizable pieces as in 3 dimensions, into symplectic manifolds, and so forth). In dimension 4 and above not all manifolds
are geometrizable, but they are an interesting class.
Conversely, one can take a high dimensional point of view on low dimensional manifolds
and ask "What does surgery predict for low dimensional manifolds?",
meaning "If surgery worked in low dimensions, what would low dimensional manifolds look like?".
One can then compare the actual theory of low dimensional manifolds
to the low dimensional analog of high dimensional manifolds,
and see if low dimensional manifolds behave "as you would expect":
in what ways do they behave like high dimensional manifolds (but for different reasons,
or via different proofs)
and in what ways are they unusual?
A connected 1-dimensional manifold is either the circle (if compact) or the real line (if not).
However, maps of 1-dimensional manifolds are a non-trivial area; see below.
. There are 3 such curvatures (positive, zero, and negative).
This is a classical result, and as stated, easy (the full uniformization theorem is subtler). The study of surfaces is deeply connected with complex analysis
and algebraic geometry
, as every orientable surface can be considered a Riemann surface
or complex algebraic curve
.
Every closed 3-dimensional manifold can be cut into pieces that are geometrizable, by the geometrization conjecture
, and there are 8 such geometries.
This is a recent result, and quite difficult. The proof (the Solution of the Poincaré conjecture) is analytic, not topological.
While the classification of surfaces is classical, maps of surfaces is an active area; see below.
they are not geometrizable (as in lower dimensions),
and surgery works topologically, but not differentiably.
Since topologically, 4-manifolds are classified by surgery,
the differentiable classification question is phrased in terms of
"differentiable structures":
"which (topological) 4-manifolds admit a differentiable structure,
and of those that do, how many?"
4-manifolds often admit many unusual differentiable structures, most strikingly the uncountably infinitely many exotic differentiable structures on R4
.
Similarly, differentiable 4-manifolds is the only remaining open case of the generalized Poincaré conjecture
.
.
The reason for dimension 5 is that the Whitney trick works in the middle dimension in dimension 5 and more: two Whitney disk
s generically don't intersect in dimension 5 and above, by general position
(
).
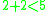In dimension 4, one can resolve intersections of two Whitney disks via Casson handle
s, which works topologically but not differentiably; see Geometric topology: Dimension for details on dimension.
More subtly, dimension 5 is the cut-off because the middle dimension has codimension
more than 2: when the codimension is 2, one encounters knot theory
, but when the codimension is more than 2, embedding theory is tractable, via the calculus of functors
. This is discussed further below.
, the classification of manifolds is one piece of understanding the category: it's classifying the objects. The other question is classifying maps of manifolds up to various equivalences, and there are many results and open questions in this area.
For maps, the appropriate notion of "low dimension" is for some purposes "self maps of low dimensional manifolds", and for other purposes "low codimension
".
, they are rigid and geometric, and in the middle (codimension 2), one has a difficult exotic theory (knot theory
).
Geometrically interesting are isometries
and isometric immersions.
Fundamental results in embeddings and immersions include:
Key tools in studying these maps are:
One may classify maps up to various equivalences:
Diffeomorphisms up to cobordism have been classified by Matthias Kreck:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically geometry and topology
Geometry and topology
In mathematics, geometry and topology is an umbrella term for geometry and topology, as the line between these two is often blurred, most visibly in local to global theorems in Riemannian geometry, and results like the Gauss–Bonnet theorem and Chern–Weil theory.Sharp distinctions between geometry...
, the classification of manifolds is a basic question, about which much is known, and many open questions remain.
Overview
- Low dimensional manifolds are classified by geometric structure; high dimensional manifolds are classified algebraically, by surgery theorySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
.
- "Low dimensions" means dimensions 2 and 3; "high dimensions" means 5 or more dimensions, or 4 or more dimensions topologically (but not smoothly); see discussion of "low" versus "high" dimension.
- Different categories of manifolds yield different classifications; these are related by the notion of "structure", and more general categories have neater theories.
- Positive curvature is constrained, negative curvature is generic.
- The abstract classification of high dimensional manifolds is ineffective: given two manifolds (presented as CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es, for instance), there is no algorithm to determine if they are isomorphic.
Different categories and additional structure
Formally, classifying manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s is classifying objects up to isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
There are many different notions of "manifold", and corresponding notions of
"map between manifolds", each of which yields a different category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and a different classification question.
These categories are related by forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
s: for instance, a differentiable manifold is also a topological manifold, and a differentiable map is also continuous, so there is a functor
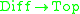.These functors are in general neither one-to-one nor onto; these failures are generally referred to in terms of "structure", as follows. A topological manifold that is in the image of
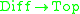is said to "admit a differentiable structure", and the fiber over a given topological manifold is "the different differentiable structures on the given topological manifold".Thus given two categories, the two natural questions are:
- Which manifolds of a given type admit an additional structure?
- If it admits an additional structure, how many does it admit?
- More precisely, what is the structure of the set of additional structures?
In more general categories, this structure set has more structure: in Diff it is simply a set, but in Top it is a group, and functorially so.
Many of these structures are G-structure
G-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
s, and the question is reduction of the structure group
Reduction of the structure group
In mathematics, in particular the theory of principal bundles, one can ask if a G-bundle "comes from" a subgroup H In mathematics, in particular the theory of principal bundles, one can ask if a...
. The most familiar example is orientability: some manifolds are orientable, some are not, and orientable manifolds admit 2 orientations.
Enumeration versus invariants
There are two usual ways to give a classification: explicitly, by an enumeration, or implicitly, in terms of invariants.For instance, for orientable surfaces,
the classification of surfaces enumerates them as the connect sum of
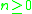tori, and an invariant that classifies them is the genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
or Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
.
Manifolds have a rich set of invariants, including:
- Point-set topology
- CompactnessCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
- ConnectednessConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
- Compactness
- Classic algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
- Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
- Fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
- Cohomology ringCohomology ringIn mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
- Euler characteristic
- Geometric topologyGeometric topologyIn mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
- normal invariants (orientabilityOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
, characteristic classes, and characteristic numbers) - Simple homotopy (Reidemeister torsion)
- Surgery theorySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
- normal invariants (orientability
Modern algebraic topology (beyond cobordism
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
theory), such as
Extraordinary (co)homology, is little-used
in the classification of manifolds, because these invariant are homotopy-invariant, and hence don't help with the finer classifications above homotopy type.
Cobordism groups (the bordism groups of a point) are computed, but the bordism groups of a space (such as
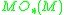) are generally not.Point-set
The point-set classification is basic—one generally fixes point-set assumptions and then studies that class of manifold.The most frequently classified class of manifolds is closed, connected manifolds.
Being homogeneous (away from any boundary), manifolds have no local point-set invariants, other than their dimension and boundary versus interior, and the most used global point-set properties are compactness and connectedness. Conventional names for combinations of these are:
- A compact manifold is a compact manifold, possibly with boundary, and not necessarily connected (but necessarily with finitely many components).
- A closed manifold is a compact manifold without boundary, not necessarily connected.
- An open manifold is a manifold without boundary (not necessarily connected), with no compact component.
For instance,
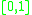is a compact manifold, 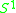is a closed manifold, and 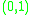is an open manifold, while 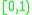is none of these.Computability
The Euler characteristic is a homologicalHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
invariant, and thus can be effectively computed given a CW structure
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
, so 2-manifolds are classified homologically.
Characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es and characteristic numbers are the corresponding generalized homological invariants, but they do not classify manifolds in higher dimension (they are not a complete set of invariants
Complete set of invariants
In mathematics, a complete set of invariants for a classification problem is a collection of mapsf_i : X \to Y_i \,, such that x ∼ x' if and only if f_i = f_i for all i...
): for instance, orientable 3-manifolds are parallelizable (Steenrod's theorem in low-dimensional topology
Low-dimensional topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology.A number of...
), so all characteristic classes vanish. In higher dimensions, characteristic classes do not in general vanish, and provide useful but not complete data.
Manifolds in dimension 4 and above cannot be effectively classified: given two n-manifolds (
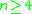) presented as CW complexCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es or handlebodies
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
, there is no algorithm for determining if they are isomorphic (homeomorphic, diffeomorphic). This is due to the unsolvability of the word problem for groups
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
, or more precisely, the triviality problem (given a finite presentation for a group, is it the trivial group?). Any finite presentation of a group can be realized as a 2-complex, and can be realized as the 2-skeleton of a 4-manifold (or higher). Thus one cannot even compute the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a given high dimensional manifold, much less a classification.
This ineffectiveness is a fundamental reason why surgery theory does not classify manifolds up to homeomorphism. Instead, for any fixed manifold M it classifies pairs (N,f) with N a manifold and f:N-->M a homotopy equivalence, two such pairs (N,f), (N',f') being regarded as equivalent if there exist a homeomorphism h:N-->N and a homotopy f'h ~ f:N-->M.
Positive curvature is constrained, negative curvature is generic
Many classical theorems in Riemannian geometry show that manifolds with positive curvature are constrained, most dramatically the 1/4-pinched sphere theoremSphere theorem
In Riemannian geometry, the sphere theorem, also known as the quarter-pinched sphere theorem, strongly restricts the topology of manifolds admitting metrics with a particular curvature bound. The precise statement of the theorem is as follows...
. Conversely, negative curvature is generic: for instance, any manifold of dimension
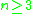admits a metric with negative Ricci curvature.This phenomenon is evident already for surfaces: there is a single orientable (and a single non-orientable) closed surface with positive curvature (the sphere and projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
),
and likewise for zero curvature (the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
and the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
), and all surfaces of higher genus admit negative curvature metrics only.
Similarly for 3-manifolds: of the 8 geometries
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
,
all but hyperbolic are quite constrained.
Overview by dimension
- Dimensions 0 and 1 are trivial.
- Low dimension manifolds (dimensions 2 and 3) admit geometry.
- Middle dimension manifolds (dimension 4 differentiably) exhibit exotic phenomena.
- High dimension manifolds (dimension 5 and more differentiably, dimension 4 and more topologically) are classified by surgery theorySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
.
Thus dimension 4 differentiable manifolds are the most complicated:
they are neither geometrizable (as in lower dimension),
nor are they classified by surgery (as in higher dimension or topologically),
and they exhibit unusual phenomena, most strikingly the uncountably infinitely many exotic differentiable structures on R4
Exotic R4
In mathematics, an exotic R4 is a differentiable manifold that is homeomorphic to the Euclidean space R4, but not diffeomorphic.The first examples were found by Robion Kirby and Michael Freedman, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's...
. Notably, differentiable 4-manifolds is the only remaining open case of the generalized Poincaré conjecture
Generalized Poincaré conjecture
In the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
.
One can take a low dimensional point of view on high dimensional manifolds
and ask "Which high dimensional manifolds are geometrizable?",
for various notions of geometrizable (cut into geometrizable pieces as in 3 dimensions, into symplectic manifolds, and so forth). In dimension 4 and above not all manifolds
are geometrizable, but they are an interesting class.
Conversely, one can take a high dimensional point of view on low dimensional manifolds
and ask "What does surgery predict for low dimensional manifolds?",
meaning "If surgery worked in low dimensions, what would low dimensional manifolds look like?".
One can then compare the actual theory of low dimensional manifolds
to the low dimensional analog of high dimensional manifolds,
and see if low dimensional manifolds behave "as you would expect":
in what ways do they behave like high dimensional manifolds (but for different reasons,
or via different proofs)
and in what ways are they unusual?
Dimensions 0 and 1: trivial
There is a unique connected 0-dimensional manifold, namely the point, and disconnected 0-dimensional manifolds are just discrete sets, classified by cardinality. They have no geometry, and their study is combinatorics.A connected 1-dimensional manifold is either the circle (if compact) or the real line (if not).
However, maps of 1-dimensional manifolds are a non-trivial area; see below.
Dimensions 2 and 3: geometrizable
Every closed 2-dimensional manifold (surface) admits a constant curvature metric, by the uniformization theoremUniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
. There are 3 such curvatures (positive, zero, and negative).
This is a classical result, and as stated, easy (the full uniformization theorem is subtler). The study of surfaces is deeply connected with complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, as every orientable surface can be considered a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
or complex algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
.
Every closed 3-dimensional manifold can be cut into pieces that are geometrizable, by the geometrization conjecture
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
, and there are 8 such geometries.
This is a recent result, and quite difficult. The proof (the Solution of the Poincaré conjecture) is analytic, not topological.
While the classification of surfaces is classical, maps of surfaces is an active area; see below.
Dimension 4: exotic
4-dimensional manifolds are the most unusual:they are not geometrizable (as in lower dimensions),
and surgery works topologically, but not differentiably.
Since topologically, 4-manifolds are classified by surgery,
the differentiable classification question is phrased in terms of
"differentiable structures":
"which (topological) 4-manifolds admit a differentiable structure,
and of those that do, how many?"
4-manifolds often admit many unusual differentiable structures, most strikingly the uncountably infinitely many exotic differentiable structures on R4
Exotic R4
In mathematics, an exotic R4 is a differentiable manifold that is homeomorphic to the Euclidean space R4, but not diffeomorphic.The first examples were found by Robion Kirby and Michael Freedman, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's...
.
Similarly, differentiable 4-manifolds is the only remaining open case of the generalized Poincaré conjecture
Generalized Poincaré conjecture
In the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
.
Dimension 5 and more: surgery
In dimension 5 and above (and 4 dimensions topologically), manifolds are classified by surgery theorySurgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
.
Whitney disk
In mathematics, given two submanifolds A and B of a manifold X intersecting in two points p and q, a Whitney disc is a mapping from the two-dimensional disc D, with two marked points, to X, such that the two marked points go to p and q, one boundary arc of D goes to A and the other to B.Their...
s generically don't intersect in dimension 5 and above, by general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
(
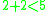).In dimension 4, one can resolve intersections of two Whitney disks via Casson handle
Casson handle
In 4-dimensional topology, a branch of mathematics, a Casson handle is a 4-dimensional topological 2-handle constructed by an infinite procedure. They are named for Andrew Casson, who introduced them in about 1973. They were originally called "flexible handles" by Casson himself, and introduced...
s, which works topologically but not differentiably; see Geometric topology: Dimension for details on dimension.
More subtly, dimension 5 is the cut-off because the middle dimension has codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
more than 2: when the codimension is 2, one encounters knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, but when the codimension is more than 2, embedding theory is tractable, via the calculus of functors
Calculus of functors
In algebraic topology, a branch of mathematics, the calculus of functors or Goodwillie calculus is a technique for studying functors by approximating them by a sequence of simpler functors; it generalizes the sheafification of a presheaf...
. This is discussed further below.
Maps between manifolds
From the point of view of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the classification of manifolds is one piece of understanding the category: it's classifying the objects. The other question is classifying maps of manifolds up to various equivalences, and there are many results and open questions in this area.
For maps, the appropriate notion of "low dimension" is for some purposes "self maps of low dimensional manifolds", and for other purposes "low codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
".
Low dimensional self-maps
- 1-dimensional: homeomorphisms of the circle
- 2-dimensional: mapping class groupMapping class groupIn mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
and Torelli group
Low codimension
Analogously to the classification of manifolds, in high codimension (meaning more than 2), embeddings are classified by surgery, while in low codimension or in relative dimensionRelative dimension
In mathematics, specifically linear algebra and geometry, relative dimension is the dual notion to codimension.In linear algebra, given a quotient map V \to Q, the difference dim V − dim Q is the relative dimension; this equals the dimension of the kernel.In fiber bundles, the relative dimension of...
, they are rigid and geometric, and in the middle (codimension 2), one has a difficult exotic theory (knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
).
- In codimension greater than 2, embeddings are classified by surgery theory.
- In codimension 2, particularly embeddings of 1-dimensional manifolds in 3-dimensional ones, one has knot theoryKnot theoryIn topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
. - In codimension 1, a codimension 1 embedding separates a manifold, and these are tractable.
- In codimension 0, a codimension 0 (proper) immersion is a covering space, which are classified algebraically, and these are more naturally thoughts of as submersions.
- In relative dimension, a submersion with compact domain is a fiber bundle (just as in codimension 0 = relative dimension 0), which are classified algebraically.
High dimensions
Particularly topologically interesting classes of maps include embeddings, immersions, and submersions.Geometrically interesting are isometries
Isometry (Riemannian geometry)
In the study of Riemannian geometry in mathematics, a local isometry from one Riemannian manifold to another is a map which pulls back the metric tensor on the second manifold to the metric tensor on the first...
and isometric immersions.
Fundamental results in embeddings and immersions include:
- Whitney embedding theorem
- Whitney immersion theorem
- Nash embedding theoremNash embedding theoremThe Nash embedding theorems , named after John Forbes Nash, state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path...
- Smale-Hirsch theorem
Key tools in studying these maps are:
- Gromov's h-principles
- Calculus of functorsCalculus of functorsIn algebraic topology, a branch of mathematics, the calculus of functors or Goodwillie calculus is a technique for studying functors by approximating them by a sequence of simpler functors; it generalizes the sheafification of a presheaf...
One may classify maps up to various equivalences:
- homotopyHomotopyIn topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
- cobordismCobordismIn mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
- concordance
- isotopy
Diffeomorphisms up to cobordism have been classified by Matthias Kreck:
- M. Kreck, Bordism of diffeomorphisms Bull. Amer. Math. Soc. Volume 82, Number 5 (1976), 759-761.
- M. Kreck, Bordism of diffeomorphisms and related topics, Springer Lect. Notes 1069 (1984)
See also
- The Berger classification of holonomyHolonomyIn differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
groups.