
Sphere theorem
Encyclopedia
In Riemannian geometry
, the sphere theorem, also known as the quarter-pinched sphere theorem, strongly restricts the topology of manifolds admitting metrics with a particular curvature bound. The precise statement of the theorem is as follows. If M is a complete, simply-connected, n-dimensional Riemannian manifold
with sectional curvature
taking values in the interval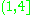 then M is homeomorphic to the n-sphere. (To be precise, we mean the sectional curvature of every tangent 2-plane at each point must lie in
then M is homeomorphic to the n-sphere. (To be precise, we mean the sectional curvature of every tangent 2-plane at each point must lie in 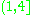 .) Another way of stating the result is that if M is not homeomorphic to the sphere, then it is impossible to put a metric on M with quarter-pinched curvature.
.) Another way of stating the result is that if M is not homeomorphic to the sphere, then it is impossible to put a metric on M with quarter-pinched curvature.
Note that the conclusion is false if the sectional curvatures are allowed to take values in the closed interval . The standard counterexample is complex projective space
. The standard counterexample is complex projective space
with the Fubini-Study metric
; sectional curvatures of this metric take on values between 1 and 4, with endpoints included. Other counterexamples may be found among the rank one symmetric spaces
.
s that are not diffeomorphic. (For more information, see the article on exotic spheres
.) However, in 2007 Simon Brendle and Richard Schoen
of Stanford University utilized Ricci flow
to prove that with the above hypotheses, M is necessarily diffeomorphic to the n-sphere with its standard smooth structure. Moreover, the proof of Brendle and Schoen only uses the weaker assumption of pointwise rather than global pinching. This result is known as the Differentiable Sphere Theorem.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the sphere theorem, also known as the quarter-pinched sphere theorem, strongly restricts the topology of manifolds admitting metrics with a particular curvature bound. The precise statement of the theorem is as follows. If M is a complete, simply-connected, n-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
taking values in the interval
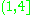 then M is homeomorphic to the n-sphere. (To be precise, we mean the sectional curvature of every tangent 2-plane at each point must lie in
then M is homeomorphic to the n-sphere. (To be precise, we mean the sectional curvature of every tangent 2-plane at each point must lie in 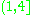 .) Another way of stating the result is that if M is not homeomorphic to the sphere, then it is impossible to put a metric on M with quarter-pinched curvature.
.) Another way of stating the result is that if M is not homeomorphic to the sphere, then it is impossible to put a metric on M with quarter-pinched curvature.Note that the conclusion is false if the sectional curvatures are allowed to take values in the closed interval
 . The standard counterexample is complex projective space
. The standard counterexample is complex projective spaceComplex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
with the Fubini-Study metric
Fubini-Study metric
In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study....
; sectional curvatures of this metric take on values between 1 and 4, with endpoints included. Other counterexamples may be found among the rank one symmetric spaces
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
.
Differentiable sphere theorem
The original proof of the sphere theorem did not conclude that M was necessarily diffeomorphic to the n-sphere. This complication is because spheres in higher dimensions admit smooth structureSmooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
s that are not diffeomorphic. (For more information, see the article on exotic spheres
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
.) However, in 2007 Simon Brendle and Richard Schoen
Richard Schoen
Richard Melvin Schoen is an American mathematician. Born in Fort Recovery, Ohio, he received his PhD in 1977 from Stanford University where he is currently the Anne T. and Robert M. Bass Professor of Humanities and Sciences...
of Stanford University utilized Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
to prove that with the above hypotheses, M is necessarily diffeomorphic to the n-sphere with its standard smooth structure. Moreover, the proof of Brendle and Schoen only uses the weaker assumption of pointwise rather than global pinching. This result is known as the Differentiable Sphere Theorem.

