Geometrization conjecture
Encyclopedia
Thurston's geometrization conjecture states that compact 3-manifold
s can be decomposed canonically into submanifold
s that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem
for surfaces. It was proposed by , and implies several other conjectures, such as the Poincaré conjecture
and Thurston's elliptization conjecture.
Thurston's hyperbolization theorem
implies that Haken manifold
s satisfy the geometrization conjecture. Thurston announced a proof in the 1980s and since then several complete proofs have appeared in print.
Grigori Perelman
sketched a proof of the full geometrization conjecture in 2003 using Ricci flow
with surgery.
There are now four different manuscripts (see below) with details of the proof. The Poincaré conjecture and the spherical space form conjecture
are corollaries of the geometrization conjecture, although there are shorter proofs of the former that do not lead to the geometrization conjecture.
Every closed 3-manifold has a prime decomposition
: this means it is the connected sum
of prime three-manifolds (this decomposition is essentially unique except for a small problem in the case of non-orientable manifolds). This reduces much of the study of 3-manifolds to the case of prime 3-manifolds: those that cannot be written as a non-trivial connected sum.
Here is a statement of Thurston's conjecture:
There are 8 possible geometric structures in 3 dimensions, described in the next section.
There is a unique minimal way of cutting an irreducible oriented 3-manifold along tori into pieces that are Seifert manifolds or atoroidal
called the JSJ decomposition
, which is not quite the same as the decomposition in the geometrization conjecture, because some of the pieces in the JSJ decomposition might not have finite volume geometric structures. (For example, the mapping torus of an Anosov map of a torus has a finite volume sol structure, but its JSJ decomposition cuts it open along one torus to produce a product of a torus and a unit interval, and the interior of this has no finite volume geometric structure.)
For non-oriented manifolds the easiest way to state a geometrization conjecture is to first take the oriented double cover. It is also possible to work directly with non-orientable manifolds, but this gives some extra complications: it may be necessary to cut along projective planes and Klein bottles as well as spheres and tori, and manifolds with a projective plane boundary component usually have no geometric structure so this gives a minor extra complication.
In 2 dimensions the analogous statement says that every surface (without boundary) has a geometric structure consisting of a metric with constant curvature; it is not necessary to cut the manifold up first.
A model geometry is called maximal if
G is maximal among groups acting smoothly and transitively on X with compact stabilizers. Sometimes this condition is included in the definition of a model geometry.
A geometric structure on a manifold M is a diffeomorphism from M to X/Γ for some model geometry X, where Γ is a discrete subgroup of G acting freely on X. If a given manifold admits a geometric structure, then it admits one whose model is maximal.
A 3-dimensional model geometry X is relevant to the geometrization conjecture if it is maximal and if there is at least one compact manifold with a geometric structure modelled on X. Thurston classified the 8 model geometries satisfying these conditions; they are listed below and are sometimes called Thurston geometries. (There are also uncountably many model geometries without compact quotients.)
There is some connection with the Bianchi groups
: the 3-dimensional Lie groups. Most Thurston geometries can be realized as a left invariant metric on a Bianchi group. However S2×R cannot be, Euclidean space corresponds to two different Bianchi groups, and there are an uncountable number of solvable non-unimodular Bianchi groups, most of which give model geometries with no compact representatives.
s.
This geometry can be modeled as a left invariant metric on the Bianchi group of type IX
.
Manifolds with this geometry are all compact, orientable, and have the structure of a Seifert fiber space
(often in several ways). The complete list of such manifolds is given in the article on Spherical 3-manifold
s.
Under Ricci flow manifolds with this geometry collapse to a point in finite time.
mapping torus
of a finite order automorphism of the 2-torus; see torus bundle
. There are exactly 10 finite closed 3-manifolds with this geometry, 6 orientable and 4 non-orientable.
This geometry can be modeled as a left invariant metric on the Bianchi groups of type I or VII0
.
Finite volume manifolds with this geometry are all compact, and have the structure of a Seifert fiber space
(sometimes in two ways). The complete list of such manifolds is given in the article on Seifert fiber space
s.
Under Ricci flow manifolds with Euclidean geometry remain invariant.
. Other examples are given by the Seifert–Weber space, or "sufficiently complicated" Dehn surgeries
on links, or most Haken manifold
s. The geometrization conjecture implies that a closed 3-manifold is hyperbolic if and only if it is irreducible, atoroidal
, and has infinite fundamental group.
This geometry can be modeled as a left invariant metric on the Bianchi group of type V
.
Under Ricci flow manifolds with hyperbolic geometry expand.
Finite volume manifolds with this geometry are all compact and have the structure of a Seifert fiber space
(often in several ways). Under normalized Ricci flow manifolds with this geometry converge to a 1-dimensional manifold.
if they are orientable. (If they are not orientable the natural fibration by circles is not necessarily a Seifert fibration: the problem is that some fibers may "reverse orientation"; in other words their neighborhoods look like fibered solid Klein bottles rather than solid tori.) The classification of such (oriented) manifolds is given in the article on Seifert fiber space
s.
This geometry can be modeled as a left invariant metric on the Bianchi group of type III
.
Under normalized Ricci flow manifolds with this geometry converge to a 2-dimensional manifold.
is the universal cover of SL2(R), which fibers over 
. The point stabilizer is O2(R). The group G has 2 components. Its identity component has the structure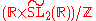 
. Examples of these manifolds include: the manifold of unit vectors of the tangent bundle of a hyperbolic surface, and more generally the Brieskorn homology spheres
(excepting the 3-sphere and the Poincare dodecahedral space). This geometry can be modeled as a left invariant metric on the Bianchi group of type VIII
. Finite volume manifolds with this geometry are orientable and have the structure of a Seifert fiber space
. The classification of such manifolds is given in the article on Seifert fiber space
s. Under normalized Ricci flow manifolds with this geometry converge to a 2-dimensional manifold.
of a 2-torus, or the quotient of the Heisenberg group by the "integral Heisenberg group".
This geometry can be modeled as a left invariant metric on the Bianchi group of type II
.
Finite volume manifolds with this geometry are compact and orientable and have the structure of a Seifert fiber space
. The classification of such manifolds is given in the article on Seifert fiber space
s.
Under normalized Ricci flow compact manifolds with this geometry converge to R2 with the flat metric.
and the geometry can be modeled as a left invariant metric on this group. All finite volume manifolds with sol geometry are compact. The compact manifolds with sol geometry are either the mapping torus
of an Anosov map of the 2-torus (an automorphism of the 2-torus given by an invertible 2 by 2 matrix whose eigenvalues are real and distinct, such as
), or quotients of these by groups of order at most 8. The eigenvalues of the automorphism of the torus generate an order of a real quadratic field, and the sol manifolds could in principle be classified in terms of the units and ideal classes of this order, though the details do not seem to be written down anywhere.
Under normalized Ricci flow compact manifolds with this geometry converge (rather slowly) to R1.
Infinite volume manifolds can have many different types of geometric structure: for example, R3 can have 6 of the different geometric structures listed above, as 6 of the 8 model geometries are homeomorphic to it. Moreover if the volume does not have to be finite there are an infinite number of new geometric structures with no compact models; for example, the geometry of almost any non-unimodular 3-dimensional Lie group.
There can be more than one way to decompose a closed 3-manifold into pieces with geometric structures. For example:
It is possible to choose a "canonical" decomposition into pieces with geometric structure, for example by first cutting the manifold into prime pieces in a minimal way, then cutting these up using the smallest possible number of tori. However this minimal decomposition is not necessarily the one produced by Ricci flow; if fact, the Ricci flow can cut up a manifold into geometric pieces in many inequivalent ways, depending on the choice of initial metric.
was awarded to Thurston in 1982 partially for his proof of the geometrization conjecture for Haken manifold
s.
The case of 3-manifolds that should be spherical has been slower, but provided the spark needed for Richard Hamilton
to develop his Ricci flow
. In 1982, Hamilton showed that given a closed 3-manifold with a metric of positive Ricci curvature, the Ricci flow would collapse the manifold to a point in finite time, which proves the geometrization conjecture for this case as the metric becomes "almost round" just before the collapse. He later developed a program to prove the geometrization conjecture by Ricci flow with surgery. The idea is that the Ricci flow will in general produce singularities, but one may be able to continue the Ricci flow past the singularity by using surgery to change the topology of the manifold. Roughly speaking, the Ricci flow contracts positive curvature regions and expands negative curvature regions, so it should kill off the pieces of the manifold with the "positive curvature" geometries S3 and S2×R, while what is left at large times should have a thick-thin decomposition into a "thick" piece with hyperbolic geometry and a "thin" graph manifold
.
In 2003 Grigori Perelman
sketched a proof of the geometrization conjecture by showing that the Ricci flow can indeed be continued past the singularities, and has the behavior described above. The main difficulty in verifying Perelman's proof of the Geometrization conjecture was a critical use of his Theorem 7.4 in the preprint 'Ricci Flow with surgery on three-manifolds'. This theorem was stated by Perelman without proof. There are now several different proofs of Perelman's Theorem 7.4, or variants of it which are sufficient to prove geometrization. There is the paper of Shioya and Yamaguchi that uses Perelman's stability theorem and a fibration theorem for Alexandrov spaces. This method, with full details leading to the proof of Geometrization, can be found in the exposition by B. Kleiner
and J. Lott in 'Notes on Perelman's papers' in the journal Geometry & Topology.
A second route to Geometrization is the method of Bessières et al., which uses Thurston's hyperbolization theorem for Haken manifolds and Gromov's norm for 3-manifolds. A book by the same authors with complete details of their version of the proof has been published by the European Mathematical Society.
Also containing proofs of Perelman's Theorem 7.4, there is a paper of Morgan and Tian,
another paper of Kleiner and Lott, and a paper by Cao and Ge.
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s can be decomposed canonically into submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
s that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
for surfaces. It was proposed by , and implies several other conjectures, such as the Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
and Thurston's elliptization conjecture.
Thurston's hyperbolization theorem
Hyperbolization theorem
In geometry, Thurston's geometrization theorem or hyperbolization theorem implies that closed atoroidal Haken manifolds are hyperbolic, and in particular satisfy the Thurston conjecture.-Statement:...
implies that Haken manifold
Haken manifold
In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
s satisfy the geometrization conjecture. Thurston announced a proof in the 1980s and since then several complete proofs have appeared in print.
Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
sketched a proof of the full geometrization conjecture in 2003 using Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
with surgery.
There are now four different manuscripts (see below) with details of the proof. The Poincaré conjecture and the spherical space form conjecture
Spherical space form conjecture
In geometric topology, the spherical space form conjecture states that a finite group acting on the 3-sphere is conjugate to a group of isometries of the 3-sphere acting by left translation....
are corollaries of the geometrization conjecture, although there are shorter proofs of the former that do not lead to the geometrization conjecture.
The conjecture
A 3-manifold is called closed if it is compact and has no boundary.Every closed 3-manifold has a prime decomposition
Prime decomposition (3-manifold)
In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique collection of prime 3-manifolds....
: this means it is the connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of prime three-manifolds (this decomposition is essentially unique except for a small problem in the case of non-orientable manifolds). This reduces much of the study of 3-manifolds to the case of prime 3-manifolds: those that cannot be written as a non-trivial connected sum.
Here is a statement of Thurston's conjecture:
- Every oriented prime closed 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
can be cut along tori, so that the interior of each of the resulting manifolds has a geometric structure with finite volume.
There are 8 possible geometric structures in 3 dimensions, described in the next section.
There is a unique minimal way of cutting an irreducible oriented 3-manifold along tori into pieces that are Seifert manifolds or atoroidal
Atoroidal
In mathematics, there are three definitions for atoroidal as applied to 3-manifolds:*A 3-manifold is atoroidal if it does not contain an embedded, non-boundary parallel, incompressible torus....
called the JSJ decomposition
JSJ decomposition
In mathematics, the JSJ decomposition, also known as the toral decomposition, is a topological construct given by the following theorem:The acronym JSJ is for William Jaco, Peter Shalen, and Klaus Johannson...
, which is not quite the same as the decomposition in the geometrization conjecture, because some of the pieces in the JSJ decomposition might not have finite volume geometric structures. (For example, the mapping torus of an Anosov map of a torus has a finite volume sol structure, but its JSJ decomposition cuts it open along one torus to produce a product of a torus and a unit interval, and the interior of this has no finite volume geometric structure.)
For non-oriented manifolds the easiest way to state a geometrization conjecture is to first take the oriented double cover. It is also possible to work directly with non-orientable manifolds, but this gives some extra complications: it may be necessary to cut along projective planes and Klein bottles as well as spheres and tori, and manifolds with a projective plane boundary component usually have no geometric structure so this gives a minor extra complication.
In 2 dimensions the analogous statement says that every surface (without boundary) has a geometric structure consisting of a metric with constant curvature; it is not necessary to cut the manifold up first.
The eight Thurston geometries
A model geometry is a simply connected smooth manifold X together with a transitive action of a Lie group G on X with compact stabilizers.A model geometry is called maximal if
G is maximal among groups acting smoothly and transitively on X with compact stabilizers. Sometimes this condition is included in the definition of a model geometry.
A geometric structure on a manifold M is a diffeomorphism from M to X/Γ for some model geometry X, where Γ is a discrete subgroup of G acting freely on X. If a given manifold admits a geometric structure, then it admits one whose model is maximal.
A 3-dimensional model geometry X is relevant to the geometrization conjecture if it is maximal and if there is at least one compact manifold with a geometric structure modelled on X. Thurston classified the 8 model geometries satisfying these conditions; they are listed below and are sometimes called Thurston geometries. (There are also uncountably many model geometries without compact quotients.)
There is some connection with the Bianchi groups
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
: the 3-dimensional Lie groups. Most Thurston geometries can be realized as a left invariant metric on a Bianchi group. However S2×R cannot be, Euclidean space corresponds to two different Bianchi groups, and there are an uncountable number of solvable non-unimodular Bianchi groups, most of which give model geometries with no compact representatives.
Spherical geometry S3
The point stabilizer is O3(R), and the group G is the 6-dimensional Lie group O4(R), with 2 components. The corresponding manifolds are exactly the closed 3-manifolds with finite fundamental group. Examples include the 3-sphere, the Poincaré homology sphere, Lens spaceLens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s.
This geometry can be modeled as a left invariant metric on the Bianchi group of type IX
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
.
Manifolds with this geometry are all compact, orientable, and have the structure of a Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
(often in several ways). The complete list of such manifolds is given in the article on Spherical 3-manifold
Spherical 3-manifold
In mathematics, a spherical 3-manifold M is a 3-manifold of the formM=S^3/\Gammawhere \Gamma is a finite subgroup of SO acting freely by rotations on the 3-sphere S^3. All such manifolds are prime, orientable, and closed...
s.
Under Ricci flow manifolds with this geometry collapse to a point in finite time.
Euclidean geometry E3
The point stabilizer is O3(R), and the group G is the 6-dimensional Lie group R3.O3(R), with 2 components. Examples are the 3-torus, and more generally themapping torus
Mapping torus
In mathematics, the mapping torus in topology of a homeomorphism f of some topological space X to itself is a particular geometric construction with f...
of a finite order automorphism of the 2-torus; see torus bundle
Torus bundle
In mathematics, in the sub-field of geometric topology, a torus bundle is a kind of surface bundle over the circle, which in turn are a class of three-manifolds.-Construction:To obtain a torus bundle: let f be an...
. There are exactly 10 finite closed 3-manifolds with this geometry, 6 orientable and 4 non-orientable.
This geometry can be modeled as a left invariant metric on the Bianchi groups of type I or VII0
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
.
Finite volume manifolds with this geometry are all compact, and have the structure of a Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
(sometimes in two ways). The complete list of such manifolds is given in the article on Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s.
Under Ricci flow manifolds with Euclidean geometry remain invariant.
Hyperbolic geometry H3
The point stabilizer is O3(R), and the group G is the 6-dimensional Lie group O1,3(R)+, with 2 components. There are enormous numbers of examples of these, and their classification is not completely understood. The example with smallest volume is the Weeks manifoldWeeks manifold
In mathematics, the Weeks manifold, sometimes called the Fomenko–Matveev–Weeks manifold, is a closed hyperbolic 3-manifold obtained by and Dehn surgeries on the Whitehead link. It has volume approximately equal to 0.9427... and showed that it has the smallest volume of any closed orientable...
. Other examples are given by the Seifert–Weber space, or "sufficiently complicated" Dehn surgeries
Dehn surgery
In topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a specific construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link...
on links, or most Haken manifold
Haken manifold
In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
s. The geometrization conjecture implies that a closed 3-manifold is hyperbolic if and only if it is irreducible, atoroidal
Atoroidal
In mathematics, there are three definitions for atoroidal as applied to 3-manifolds:*A 3-manifold is atoroidal if it does not contain an embedded, non-boundary parallel, incompressible torus....
, and has infinite fundamental group.
This geometry can be modeled as a left invariant metric on the Bianchi group of type V
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
.
Under Ricci flow manifolds with hyperbolic geometry expand.
The geometry of S2×R
The point stabilizer is O2(R)×Z/2Z, and the group G is O3(R)×R.Z/2Z, with 4 components. The four finite volume manifolds with this geometry are: S2×S1, the mapping torus of the antipode map of S2, the connected sum of two copies of 3 dimensional projective space, and the product of S1 with two-dimensional projective space. The first two are mapping tori of the identity map and antipode map of the 2-sphere, and are the only examples of 3-manifolds that are prime but not irreducible. The third is the only example of a non-trivial connected sum with a geometric structure. This is the only model geometry that cannot be realized as a left invariant metric on a 3-dimensional Lie group.Finite volume manifolds with this geometry are all compact and have the structure of a Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
(often in several ways). Under normalized Ricci flow manifolds with this geometry converge to a 1-dimensional manifold.
The geometry of H2×R
The point stabilizer is O2(R) × Z/2Z, and the group G is O1,2(R)+ × R.Z/2Z, with 4 components. Examples include the product of a hyperbolic surface with a circle, or more generally the mapping torus of an isometry of a hyperbolic surface. Finite volume manifolds with this geometry have the structure of a Seifert fiber spaceSeifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
if they are orientable. (If they are not orientable the natural fibration by circles is not necessarily a Seifert fibration: the problem is that some fibers may "reverse orientation"; in other words their neighborhoods look like fibered solid Klein bottles rather than solid tori.) The classification of such (oriented) manifolds is given in the article on Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s.
This geometry can be modeled as a left invariant metric on the Bianchi group of type III
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
.
Under normalized Ricci flow manifolds with this geometry converge to a 2-dimensional manifold.
The geometry of the universal cover of SL2(R)
is the universal cover of SL2(R), which fibers over . The point stabilizer is O2(R). The group G has 2 components. Its identity component has the structure 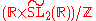. Examples of these manifolds include: the manifold of unit vectors of the tangent bundle of a hyperbolic surface, and more generally the Brieskorn homology spheresHomology sphere
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
(excepting the 3-sphere and the Poincare dodecahedral space). This geometry can be modeled as a left invariant metric on the Bianchi group of type VIII
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
. Finite volume manifolds with this geometry are orientable and have the structure of a Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
. The classification of such manifolds is given in the article on Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s. Under normalized Ricci flow manifolds with this geometry converge to a 2-dimensional manifold.
Nil geometry
This fibers over E2, and is the geometry of the Heisenberg group. The point stabilizer is O2(R). The group G has 2 components, and is a semidirect product of the 3-dimensional Heisenberg group by the group O2(R) of isometries of a circle. Compact manifolds with this geometry include the mapping torus of a Dehn twistDehn twist
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface .-Definition:...
of a 2-torus, or the quotient of the Heisenberg group by the "integral Heisenberg group".
This geometry can be modeled as a left invariant metric on the Bianchi group of type II
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
.
Finite volume manifolds with this geometry are compact and orientable and have the structure of a Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
. The classification of such manifolds is given in the article on Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s.
Under normalized Ricci flow compact manifolds with this geometry converge to R2 with the flat metric.
Sol geometry
This geometry fibers over the line with fiber the plane, and is the geometry of the identity component of the group G. The point stabilizer is the dihedral group of order 8. The group G has 8 components, and is the group of maps from 2-dimensional Minkowski space to itself that are either isometries or multiply the metric by −1. The identity component has a normal subgroup R2 with quotient R, where R acts on R2 with 2 (real) eigenspaces, with distinct real eigenvalues of product 1. This is the Bianchi group of type VI0Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
and the geometry can be modeled as a left invariant metric on this group. All finite volume manifolds with sol geometry are compact. The compact manifolds with sol geometry are either the mapping torus
Mapping torus
In mathematics, the mapping torus in topology of a homeomorphism f of some topological space X to itself is a particular geometric construction with f...
of an Anosov map of the 2-torus (an automorphism of the 2-torus given by an invertible 2 by 2 matrix whose eigenvalues are real and distinct, such as
), or quotients of these by groups of order at most 8. The eigenvalues of the automorphism of the torus generate an order of a real quadratic field, and the sol manifolds could in principle be classified in terms of the units and ideal classes of this order, though the details do not seem to be written down anywhere.Under normalized Ricci flow compact manifolds with this geometry converge (rather slowly) to R1.
Uniqueness
A closed 3-manifold has a geometric structure of at most one of the 8 types above, but finite volume non-compact 3-manifolds can occasionally have more than one type of geometric structure. (However a manifold can have many different geometric structures of the same type; for example, a surface of genus at least 2 has a continuum of different hyperbolic metrics.) More precisely, if M is a manifold with a finite volume geometric structure, then the type of geometric structure is almost determined as follows, in terms of the fundamental group π1(M):- If π1(M) is finite then the geometric structure on M is spherical, and M is compact.
- If π1(M) is virtually cyclic but not finite then the geometric structure on M is S2×R, and M is compact.
- If π1(M) is virtually abelian but not virtually cyclic then the geometric structure on M is Euclidean, and M is compact.
- If π1(M) is virtually nilpotent but not virtually abelian then the geometric structure on M is nil geometry, and M is compact.
- If π1(M) is virtually solvable but not virtually nilpotent then the geometric structure on M is sol geometry, and M is compact.
- If π1(M) has an infinite normal cyclic subgroup but is not virtually solvable then the geometric structure on M is either H2×R or the universal cover of SL2(R). The manifold M may be either compact or non-compact. If it is compact, then the 2 geometries can be distinguished by whether or not π1(M) has a finite indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
subgroup that splits as a semidirect product of the normal cyclic subgroup and something else. If the manifold is non-compact, then the fundamental group cannot distinguish the two geometries, and there are examples (such as the complement of a trefoil knot) where a manifold may have a finite volume geometric structure of either type. - If π1(M) has no infinite normal cyclic subgroup and is not virtually solvable then the geometric structure on M is hyperbolic, and M may be either compact or non-compact.
Infinite volume manifolds can have many different types of geometric structure: for example, R3 can have 6 of the different geometric structures listed above, as 6 of the 8 model geometries are homeomorphic to it. Moreover if the volume does not have to be finite there are an infinite number of new geometric structures with no compact models; for example, the geometry of almost any non-unimodular 3-dimensional Lie group.
There can be more than one way to decompose a closed 3-manifold into pieces with geometric structures. For example:
- Taking connected sums with several copies of S3 does not change a manifold.
- The connected sum of two projective 3-spaces has a S2×R geometry, and is also the connected sum of two pieces with S3 geometry.
- The product of a surface negative curvature and a circle has a geometric structure, but can also be cut along tori to produce smaller pieces that also have geometric structures. There are many similar examples for Seifert fiber spaces.
It is possible to choose a "canonical" decomposition into pieces with geometric structure, for example by first cutting the manifold into prime pieces in a minimal way, then cutting these up using the smallest possible number of tori. However this minimal decomposition is not necessarily the one produced by Ricci flow; if fact, the Ricci flow can cut up a manifold into geometric pieces in many inequivalent ways, depending on the choice of initial metric.
History
The Fields MedalFields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
was awarded to Thurston in 1982 partially for his proof of the geometrization conjecture for Haken manifold
Haken manifold
In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
s.
The case of 3-manifolds that should be spherical has been slower, but provided the spark needed for Richard Hamilton
Richard Hamilton (professor)
Richard Streit Hamilton is Davies Professor of mathematics at Columbia University.He received his B.A in 1963 from Yale University and Ph.D. in 1966 from Princeton University. Robert Gunning supervised his thesis...
to develop his Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
. In 1982, Hamilton showed that given a closed 3-manifold with a metric of positive Ricci curvature, the Ricci flow would collapse the manifold to a point in finite time, which proves the geometrization conjecture for this case as the metric becomes "almost round" just before the collapse. He later developed a program to prove the geometrization conjecture by Ricci flow with surgery. The idea is that the Ricci flow will in general produce singularities, but one may be able to continue the Ricci flow past the singularity by using surgery to change the topology of the manifold. Roughly speaking, the Ricci flow contracts positive curvature regions and expands negative curvature regions, so it should kill off the pieces of the manifold with the "positive curvature" geometries S3 and S2×R, while what is left at large times should have a thick-thin decomposition into a "thick" piece with hyperbolic geometry and a "thin" graph manifold
Graph manifold
In topology, a graph manifold is a 3-manifold which is obtained by gluing some circle bundles. They were invented and classified by the German topologist Friedhelm Waldhausen in 1967...
.
In 2003 Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
sketched a proof of the geometrization conjecture by showing that the Ricci flow can indeed be continued past the singularities, and has the behavior described above. The main difficulty in verifying Perelman's proof of the Geometrization conjecture was a critical use of his Theorem 7.4 in the preprint 'Ricci Flow with surgery on three-manifolds'. This theorem was stated by Perelman without proof. There are now several different proofs of Perelman's Theorem 7.4, or variants of it which are sufficient to prove geometrization. There is the paper of Shioya and Yamaguchi that uses Perelman's stability theorem and a fibration theorem for Alexandrov spaces. This method, with full details leading to the proof of Geometrization, can be found in the exposition by B. Kleiner
Bruce Kleiner
Bruce Alan Kleiner is an American mathematician, working in differential geometry and topology and geometric group theory.He received his Ph.D. in 1990 from the University of California, Berkeley. His advisor was Wu-Yi Hsiang. He is now Professor of Mathematics at New York University.Kleiner has...
and J. Lott in 'Notes on Perelman's papers' in the journal Geometry & Topology.
A second route to Geometrization is the method of Bessières et al., which uses Thurston's hyperbolization theorem for Haken manifolds and Gromov's norm for 3-manifolds. A book by the same authors with complete details of their version of the proof has been published by the European Mathematical Society.
Also containing proofs of Perelman's Theorem 7.4, there is a paper of Morgan and Tian,
another paper of Kleiner and Lott, and a paper by Cao and Ge.
External links
- The Geometry of 3-Manifolds(video) A public lecture on the Poincaré and geometrization conjectures, given by C. McMullen at Harvard in 2006.