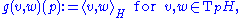Hilbert manifold
Encyclopedia
In mathematics
, a Hilbert manifold is a manifold
modeled on Hilbert spaces. Thus it is a separable Hausdorff space
in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space
. The concept of a Hilbert manifold provides a possibility of extending the theory of manifolds to infinite-dimensional setting. Analogously to the finite-dimensional situation, one can define a differentiable Hilbert manifold by considering a maximal atlas in which the transition maps are differentiable.
of a manifold and a tubular neighbourhood of a submanifold
(of finite codimension) carry over from the finite dimensional situation to the Hilbert setting with little change. However, in statements involving maps between manifolds, one often has to restrict consideration to Fredholm maps, i.e. maps whose differential at every point is Fredholm
. The reason for this is that Sard's lemma
holds for Fredholm maps, but not in general. Notwithstanding this difference, Hilbert manifolds have several very nice properties.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Hilbert manifold is a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
modeled on Hilbert spaces. Thus it is a separable Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. The concept of a Hilbert manifold provides a possibility of extending the theory of manifolds to infinite-dimensional setting. Analogously to the finite-dimensional situation, one can define a differentiable Hilbert manifold by considering a maximal atlas in which the transition maps are differentiable.
Properties
Many basic constructions of the manifold theory, such as the tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of a manifold and a tubular neighbourhood of a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
(of finite codimension) carry over from the finite dimensional situation to the Hilbert setting with little change. However, in statements involving maps between manifolds, one often has to restrict consideration to Fredholm maps, i.e. maps whose differential at every point is Fredholm
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
. The reason for this is that Sard's lemma
Sard's lemma
Sard's theorem, also known as Sard's lemma or the Morse–Sard theorem, is a result in mathematical analysis which asserts that the image of the set of critical points of a smooth function f from one Euclidean space or manifold to another has Lebesgue measure 0 – they form a null set...
holds for Fredholm maps, but not in general. Notwithstanding this difference, Hilbert manifolds have several very nice properties.
- Kuiper's theoremKuiper's theoremIn mathematics, Kuiper's theorem is a result on the topology of operators on an infinite-dimensional, complex Hilbert space H...
: If X is a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
or has the homotopy type of a CW-Complex then every (real or complex) Hilbert space bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over X is trivial. In particular, every Hilbert manifold is parallelizable. - Every smooth Hilbert manifold can be smoothly embedded onto an open subset of the model Hilbert space.
- Every homotopy equivalence between two Hilbert manifolds is homotopic to a diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
. In particular every two homotopy equivalent Hilbert manifolds are already diffeomorphic. This stands in contrast to lens spaceLens spaceA lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s and exotic sphereExotic sphereIn differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s, which demonstrate that in the finite-dimensional situation, homotopy equivalence, homeomorphism, and diffeomorphism of manifolds are distinct properties. - Although Sard's Theorem does not hold in general, every continuous map f : X → Rn from a Hilbert manifold can be arbitrary closely approximated by a smooth map g : X → Rn which has no critical pointsCritical point (mathematics)In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
Examples
- Any Hilbert space H is a Hilbert manifold with a single global chart given by the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on H. Moreover, since H is a vector space, the tangent space TpH to H at any point p ∈ H is canonically isomorphic to H itself, and so has a natural inner product, the "same" as the one on H. Thus, H can be given the structure of a Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with metric
- where ⟨·, ·⟩H denotes the inner product in H.
- Similarly, any open subsetOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of a Hilbert space is a Hilbert manifold and a Riemannian manifold under the same construction as for the whole space.
- There are several mapping spacesFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
between manifolds which can be viewed as Hilbert spaces by only considering maps of suitable Sobolev classSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
. For example we can consider the space LM of all H1 maps from the unit circle S1 into a manifold M. This can be topologized via the compact open topology as a subspace of the space of all continuous mappings from the circle to M, i.e. the free loop space of M. The Sobolev kind mapping space LM described above is homotopy equivalent to the free loop space. This makes it suited to the study of algebraic topology of the free loop space, especially in the field of string topologyString topologyString topology, a branch of mathematics, is the study of algebraic structures on the homology of free loop spaces. The field was started by Chas and Sullivan in 1999 .-Motivation:...
. We can do an analogous Sobolev construction for the loop space, making it a codimensionCodimensionIn mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
d Hilbert submanifold of LM, where d is the dimension of M.