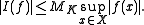Radon measure
Encyclopedia
In mathematics
(specifically, measure theory), a Radon measure, named after Johann Radon
, is a measure
on the σ-algebra of Borel set
s of a Hausdorff topological space X that is locally finite
and inner regular
.
that is compatible with the topology in some sense. One way to do this is to define a measure on the Borel set
s of the topological space. In general there are several problems with this: for example, such a measure may not have a well defined support
. Another approach to measure theory is to restrict to locally compact
Hausdorff space
s, and only consider the measures that correspond to positive linear functional
s on the space of continuous function
s with compact support (some authors use this as the definition of a Radon measure). This produces a good theory with no pathological problems, but does not apply to spaces that are not locally compact.
The theory of Radon measures has most of the good properties of the usual theory for locally compact spaces, but applies to all Hausdorff topological spaces. The idea of the definition of a Radon measure is to find some properties that characterize the measures on locally compact spaces corresponding to positive functionals, and use these properties as the definition of a Radon measure on an arbitrary Hausdorff space.
The measure m is called inner regular or tight if m(B) is the supremum
of m(K) for K a compact set contained in the Borel set B.
The measure m is called outer regular if m(B) is the infimum
of m(U) for U an open set containing the Borel set B.
The measure m is called locally finite if every point has a neighborhood of finite measure.
The measure m is called a Radon measure if it is inner regular and locally finite.
(It is possible to extend the theory of Radon measures to non-Hausdorff spaces, essentially by replacing the word "compact" by "closed compact" everywhere. However, there seem to be almost no applications of this extension.)
linear functionals on the space of continuous function
s with compact support. This makes it possible to develop measure and integration in terms of functional analysis
, an approach taken by and a number of other authors.
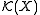, which can be given a natural locally convex topology. Indeed, 
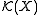is the union of the spaces 
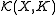of continuous functions with support contained in compact
sets K. Each of the spaces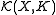
carries naturally the topology of uniform convergence, which makes it into a Banach space
. But as a union of topological spaces is a special case of a direct limit
of topological spaces, the space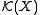
can be equipped with the direct limit topology induced by the spaces 
.
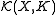If m is a Radon measure on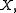
then the mapping
is a continuous positive linear map from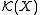
to R. Positivity means that I(f) ≥ 0 whenever f is a non-negative function. Continuity with respect to the direct limit topology defined above is equivalent to the following condition: for every compact subset K of X there exists a constant MK such that, for every continuous real-valued function f on X with support contained in K,
Conversely, by the Riesz representation theorem
, each positive linear form on
arises as integration with respect to a Radon measure and is thus a continuous positive linear form on 
.
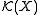A real-valued Radon measure is defined to be any continuous linear form on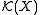
; they are precisely the differences of two Radon measures. This gives an identification of real-valued Radon measures with the dual space
of the locally convex space
. These real-valued Radon measures need not be signed measure
s. For example, sin(x)dx is a real-valued Radon measure, but is not even an extended signed measure as it cannot be written as the difference of two measures at least one of which is finite.
Some authors use the preceding approach to define (positive) Radon measures to be the positive linear forms on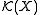
; see , or . In this set-up it is common to use a terminology in which Radon measures in the above sense are called positive measures and real-valued Radon measures as above are called (real) measures.
It is possible to verify that these steps produce a theory identical with the one that starts from a Radon measure defined as a function that assigns a number to each Borel set
of X.
The Lebesgue measure
on R can be introduced by a few ways in this functional-analytic set-up. First, it is possibly to rely on an "elementary" integral such as the Daniell integral
or the Riemann integral
for integrals of continuous functions with compact support, as these are integrable for all the elementary definitions of integrals. The measure (in the sense defined above) defined by elementary integration is precisely the Lebesgue measure. Second, if one wants to avoid reliance on Riemann or Daniell integral or other similar theories, it is possible to develop first the general theory of Haar measure
s and define the Lebesgue measure as the Haar measure λ on R that satisfies the normalisation condition λ([0,1])=1.
The following are not examples of Radon measures:
M (on the Borel sets) by putting
The measure M is outer regular, and locally finite, and inner regular for open sets. It coincides with m on compact and open sets, and m can be reconstructed from M as the unique inner regular measure that is the same as M on compact sets. The measure m is called moderated if M is σ-finite; in this case the measures m and M are the same. (If m is σ-finite this does not imply that M is σ-finite, so being moderated is stronger than being σ-finite.)
On a strongly Lindelof space every Radon measure is moderated.
of all (positive) Radon measures on 
can be given the structure of a complete
metric space
by defining the Radon distance between two measures
to be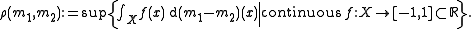
This metric has some limitations. For example, the space of Radon probability measure
s on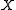
,
is not sequentially compact
with respect to the Radon metric: i.e., it is not guaranteed that any sequence of probability measures will have a subsequence that is convergent with respect to the Radon metric, which presents difficulties in certain applications. On the other hand, if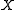
is a compact metric space, then the
Wasserstein metric
turns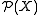
into a compact metric space.
Convergence in the Radon metric implies weak convergence of measures: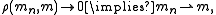
but the converse implication is false in general. Convergence of measures in the Radon metric is sometimes known as strong convergence, as contrasted with weak convergence.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
(specifically, measure theory), a Radon measure, named after Johann Radon
Johann Radon
Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...
, is a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the σ-algebra of Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s of a Hausdorff topological space X that is locally finite
Locally finite measure
In mathematics, a locally finite measure is a measure for which every point of the measure space has a neighbourhood of finite measure.-Definition:...
and inner regular
Inner regular measure
In mathematics, an inner regular measure is one for which the measure of a set can be approximated from within by compact subsets.-Definition:...
.
Motivation
A common problem is to find a good notion of a measure on a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that is compatible with the topology in some sense. One way to do this is to define a measure on the Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s of the topological space. In general there are several problems with this: for example, such a measure may not have a well defined support
Support (measure theory)
In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
. Another approach to measure theory is to restrict to locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s, and only consider the measures that correspond to positive linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s on the space of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s with compact support (some authors use this as the definition of a Radon measure). This produces a good theory with no pathological problems, but does not apply to spaces that are not locally compact.
The theory of Radon measures has most of the good properties of the usual theory for locally compact spaces, but applies to all Hausdorff topological spaces. The idea of the definition of a Radon measure is to find some properties that characterize the measures on locally compact spaces corresponding to positive functionals, and use these properties as the definition of a Radon measure on an arbitrary Hausdorff space.
Definitions
We let m be a measure on the σ-algebra of Borel sets of a Hausdorff topological space X.The measure m is called inner regular or tight if m(B) is the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of m(K) for K a compact set contained in the Borel set B.
The measure m is called outer regular if m(B) is the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of m(U) for U an open set containing the Borel set B.
The measure m is called locally finite if every point has a neighborhood of finite measure.
The measure m is called a Radon measure if it is inner regular and locally finite.
(It is possible to extend the theory of Radon measures to non-Hausdorff spaces, essentially by replacing the word "compact" by "closed compact" everywhere. However, there seem to be almost no applications of this extension.)
Radon measures on locally compact spaces
When the underlying measure space is a locally compact topological space, the definition of a Radon measure can be expressed in terms of continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
linear functionals on the space of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s with compact support. This makes it possible to develop measure and integration in terms of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, an approach taken by and a number of other authors.
Measures
In what follows X denotes a locally compact topological space. The continuous real-valued functions with compact support on X form a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
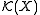, which can be given a natural locally convex topology. Indeed, 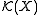is the union of the spaces 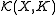of continuous functions with support contained in compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
sets K. Each of the spaces
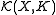carries naturally the topology of uniform convergence, which makes it into a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. But as a union of topological spaces is a special case of a direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of topological spaces, the space
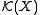can be equipped with the direct limit topology induced by the spaces 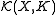.If m is a Radon measure on
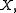then the mapping
is a continuous positive linear map from
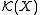to R. Positivity means that I(f) ≥ 0 whenever f is a non-negative function. Continuity with respect to the direct limit topology defined above is equivalent to the following condition: for every compact subset K of X there exists a constant MK such that, for every continuous real-valued function f on X with support contained in K,
Conversely, by the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, each positive linear form on
arises as integration with respect to a Radon measure and is thus a continuous positive linear form on 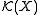.A real-valued Radon measure is defined to be any continuous linear form on
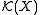; they are precisely the differences of two Radon measures. This gives an identification of real-valued Radon measures with the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the locally convex space
. These real-valued Radon measures need not be signed measureSigned measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
s. For example, sin(x)dx is a real-valued Radon measure, but is not even an extended signed measure as it cannot be written as the difference of two measures at least one of which is finite.
Some authors use the preceding approach to define (positive) Radon measures to be the positive linear forms on
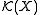; see , or . In this set-up it is common to use a terminology in which Radon measures in the above sense are called positive measures and real-valued Radon measures as above are called (real) measures.Integration
To complete the buildup of measure theory for locally compact spaces from the functional-analytic viewpoint, it is necessary to extend measure (integral) from compactly supported continuous functions. This can be done for real or complex-valued functions in several steps as follows:- Definition of the upper integral μ*(g) of a lower semicontinuous positive (real-valued) function g as the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
(possibly infinite) of the positive numbers μ(h) for compactly supported continuous functions h ≤ g - Definition of the upper integral μ*(f) for an arbitrary positive (real-valued) function f as the infimum of upper integrals μ*(g) for lower semi-continuous functions g≥f
- Definition of the vector space F = F(X,μ) as the space of all functions f on X for which the upper integral μ*(|f|) of the absolute value is finite; the upper integral of the absolute value defines a semi-norm on F, and F is a complete spaceComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
with respect to the topology defined by the semi-norm - Definition of the space L1(X,μ) of integrable functions as the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
inside F of the space of continuous compactly supported functions - Definition of the integral for functions in L1(X,μ) as extension by continuity (after verifying that μ is continuous with respect to the topology of L1(X,μ))
- Definition of the measure of a set as the integral (when it exists) of the indicator function of the set.
It is possible to verify that these steps produce a theory identical with the one that starts from a Radon measure defined as a function that assigns a number to each Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
of X.
The Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on R can be introduced by a few ways in this functional-analytic set-up. First, it is possibly to rely on an "elementary" integral such as the Daniell integral
Daniell integral
In mathematics, the Daniell integral is a type of integration that generalizes the concept of more elementary versions such as the Riemann integral to which students are typically first introduced...
or the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
for integrals of continuous functions with compact support, as these are integrable for all the elementary definitions of integrals. The measure (in the sense defined above) defined by elementary integration is precisely the Lebesgue measure. Second, if one wants to avoid reliance on Riemann or Daniell integral or other similar theories, it is possible to develop first the general theory of Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
s and define the Lebesgue measure as the Haar measure λ on R that satisfies the normalisation condition λ([0,1])=1.
Examples
The following are all examples of Radon measures:- Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on Euclidean space; - Haar measureHaar measureIn mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
on any locally compact topological group; - Dirac measure on any topological space;
- Gaussian measureGaussian measureIn mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
on Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
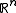with its Borel topology and sigma algebra; - Probability measureProbability measureIn mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s on the σ-algebra of Borel setBorel setIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s of any Polish spacePolish spaceIn the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
. This example not only generalizes the previous example, but includes many measures on non-locally compact spaces, such as Wiener measure on the space of real-valued continuous functions on the interval [0,1].
The following are not examples of Radon measures:
- Counting measureCounting measureIn mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
on Euclidean space is an example of a measure that is not a Radon measure, since it is not locally finite. - The space of ordinalsOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
at most equal to the first uncountable ordinalFirst uncountable ordinalIn mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
with the order topologyOrder topologyIn mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
is a compact topological space. The measure which equals 1 on any set that contains an uncountable closed set, and 0 otherwise, is Borel but not Radon. - Let X be the interval [0,1) equipped with the topology generated by the collection of half open intervals
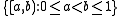. On this metric space, standard Lebesgue measure is not Radon since it is not inner regular, since compact sets are at most countable.
Moderated Radon measures
Given a Radon measure m on a space X, we can define another measureM (on the Borel sets) by putting
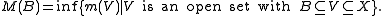
The measure M is outer regular, and locally finite, and inner regular for open sets. It coincides with m on compact and open sets, and m can be reconstructed from M as the unique inner regular measure that is the same as M on compact sets. The measure m is called moderated if M is σ-finite; in this case the measures m and M are the same. (If m is σ-finite this does not imply that M is σ-finite, so being moderated is stronger than being σ-finite.)
On a strongly Lindelof space every Radon measure is moderated.
Radon spaces
A space is called a Radon space if every finite Borel measure is a Radon measure, and strongly Radon if every locally finite Borel measure is a Radon measure. Any Suslin space is strongly Radon, and moreover every Radon measure is moderated.Duality
On a locally compact Hausdorff space, Radon measures correspond to positive linear functionals on the space of continuous functions with compact support. This is not surprising as this property is the main motivation for the definition of Radon measure.Metric space structure
The pointed coneCone (linear algebra)
In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
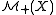of all (positive) Radon measures on 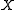can be given the structure of a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
by defining the Radon distance between two measures
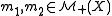to be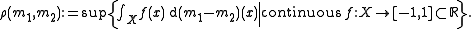This metric has some limitations. For example, the space of Radon probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s on
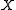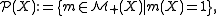
,is not sequentially compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
with respect to the Radon metric: i.e., it is not guaranteed that any sequence of probability measures will have a subsequence that is convergent with respect to the Radon metric, which presents difficulties in certain applications. On the other hand, if
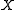is a compact metric space, then theWasserstein metric
Wasserstein metric
In mathematics, the Wasserstein metric is a distance function defined between probability distributions on a given metric space M....
turns
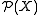into a compact metric space.Convergence in the Radon metric implies weak convergence of measures:
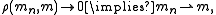
but the converse implication is false in general. Convergence of measures in the Radon metric is sometimes known as strong convergence, as contrasted with weak convergence.