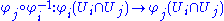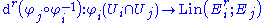Banach manifold
Encyclopedia
In mathematics
, a Banach manifold is a manifold
modeled on Banach spaces. Thus it is a topological space
in which each point has a neighbourhood
homeomorphic to an open set
in a Banach space (a more involved and formal definition is given below). Banach manifolds are one possibility of extending manifolds to infinite dimension
s.
A further generalisation is to Fréchet manifold
s, replacing Banach spaces by Fréchet space
s. On the other hand, a Hilbert manifold
is a special case of a Banach manifold in which the manifold is locally modelled on Hilbert space
s.
of class Cr, r ≥ 0, on X is a collection of pairs (called charts) (Ui, φi), i ∈ I, such that
One can then show that there is a unique topology
on X such that each Ui is open and each φi is a homeomorphism. Very often, this topological space is assumed to be a Hausdorff space
, but this is not necessary from the point of view of the formal definition.
If all the Banach spaces Ei are equal to the same space E, the atlas is called an E-atlas. However, it is not a priori necessary that the Banach spaces Ei be the same space, or even isomorphic as topological vector space
s. However, if two charts (Ui, φi) and (Uj, φj) are such that Ui and Uj have a non-empty intersection
, a quick examination of the derivative
of the crossover map
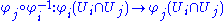
shows that Ei and Ej must indeed be isomorphic as topological vector spaces. Furthermore, the set of points x ∈ X for which there is a chart (Ui, φi) with x in Ui and Ei isomorphic to a given Banach space E is both open and closed. Hence, one can without loss of generality assume that, on each connected component
of X, the atlas is an E-atlas for some fixed E.
A new chart (U, φ) is called compatible with a given atlas { (Ui, φi) | i ∈ I } if the crossover map

is an r-times continuously differentiable function for every i ∈ I. Two atlases are called compatible if every chart in one is compatible with the other atlas. Compatibility defines an equivalence relation
on the class of all possible atlases on X.
A Cr-manifold structure on X is then defined to be a choice of equivalence class of atlases on X of class Cr. If all the Banach spaces Ei are isomorphic as topological vector spaces (which is guaranteed to be the case if X is connected
), then an equivalent atlas can be found for which they are all equal to some Banach space E. X is then called an E-manifold, or one says that X is modeled on E.
” Banach manifolds up to homeomorphism quite nicely. A 1969 theorem of David Henderson states that every infinite-dimensional, separable, metric
Banach manifold X can be embedded
as an open subset of the infinite-dimensional, separable Hilbert space, H (up to linear isomorphism, there is only one such space). In fact, Henderson's result is stronger: the same conclusion holds for any metric manifold modeled on a separable infinite-dimensional Fréchet space
.
The embedding homeomorphism can be used as a global chart for X. Thus, in the infinite-dimensional, separable, metric case, the “only” Banach manifolds are the open subsets of Hilbert space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Banach manifold is a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
modeled on Banach spaces. Thus it is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
in which each point has a neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
homeomorphic to an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in a Banach space (a more involved and formal definition is given below). Banach manifolds are one possibility of extending manifolds to infinite dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s.
A further generalisation is to Fréchet manifold
Fréchet manifold
In mathematics, in particular in nonlinear analysis, a Fréchet manifold is a topological space modeled on a Fréchet space in much the same way as a manifold is modeled on a Euclidean space....
s, replacing Banach spaces by Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s. On the other hand, a Hilbert manifold
Hilbert manifold
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of...
is a special case of a Banach manifold in which the manifold is locally modelled on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s.
Definition
Let X be a set. An atlasAtlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
of class Cr, r ≥ 0, on X is a collection of pairs (called charts) (Ui, φi), i ∈ I, such that
- each Ui is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of X and the unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the Ui is the whole of X; - each φi is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from Ui onto an open subset φi(Ui) of some Banach space Ei, and for any i and j, φi(Ui ∩ Uj) is open in Ei; - the crossover map
- is an r-times continuously differentiableSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
function for every i and j in I, i.e. the rth Fréchet derivativeFréchet derivativeIn mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
- exists and is a continuous function with respect to the Ei-normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on subsets of Ei and the operator normOperator normIn mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
topology on Lin(Eir; Ej.)
One can then show that there is a unique topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on X such that each Ui is open and each φi is a homeomorphism. Very often, this topological space is assumed to be a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, but this is not necessary from the point of view of the formal definition.
If all the Banach spaces Ei are equal to the same space E, the atlas is called an E-atlas. However, it is not a priori necessary that the Banach spaces Ei be the same space, or even isomorphic as topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s. However, if two charts (Ui, φi) and (Uj, φj) are such that Ui and Uj have a non-empty intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, a quick examination of the derivative
Derivative (generalizations)
The derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, and geometry.- Derivatives in analysis :...
of the crossover map
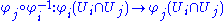
shows that Ei and Ej must indeed be isomorphic as topological vector spaces. Furthermore, the set of points x ∈ X for which there is a chart (Ui, φi) with x in Ui and Ei isomorphic to a given Banach space E is both open and closed. Hence, one can without loss of generality assume that, on each connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of X, the atlas is an E-atlas for some fixed E.
A new chart (U, φ) is called compatible with a given atlas { (Ui, φi) | i ∈ I } if the crossover map

is an r-times continuously differentiable function for every i ∈ I. Two atlases are called compatible if every chart in one is compatible with the other atlas. Compatibility defines an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the class of all possible atlases on X.
A Cr-manifold structure on X is then defined to be a choice of equivalence class of atlases on X of class Cr. If all the Banach spaces Ei are isomorphic as topological vector spaces (which is guaranteed to be the case if X is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
), then an equivalent atlas can be found for which they are all equal to some Banach space E. X is then called an E-manifold, or one says that X is modeled on E.
Examples
- If (X, || ||) is a Banach space, then X is a Banach manifold with an atlas containing a single, globally-defined chart (the identity mapIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
). - Similarly, if U is an open subset of some Banach space, then U is a Banach manifold. (See the classification theorem below.)
Classification up to homeomorphism
It is by no means true that a finite-dimensional manifold of dimension n is globally homeomorphic to Rn, or even an open subset of Rn. However, in an infinite-dimensional setting, it is possible to classify “well-behavedWell-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
” Banach manifolds up to homeomorphism quite nicely. A 1969 theorem of David Henderson states that every infinite-dimensional, separable, metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
Banach manifold X can be embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
as an open subset of the infinite-dimensional, separable Hilbert space, H (up to linear isomorphism, there is only one such space). In fact, Henderson's result is stronger: the same conclusion holds for any metric manifold modeled on a separable infinite-dimensional Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
.
The embedding homeomorphism can be used as a global chart for X. Thus, in the infinite-dimensional, separable, metric case, the “only” Banach manifolds are the open subsets of Hilbert space.