Tetrad formalism
Encyclopedia
The tetrad formalism is a non-coordinate approach to General Relativity
.
In the tetrad formalism all tensors are represented in terms of a chosen basis, a set of four vector
s called the tetrad. (When applied to theories with other than four dimensions, this approach is given other names; see also Cartan formalism). As a formalism
rather than a separate theory, it does not make different predictions but does allow the relevant equations to be expressed differently.
The advantage of the tetrad formalism over the standard coordinate-based approach to GR lies in the ability to choose the tetrad basis to reflect important physical aspects of the spacetime.
s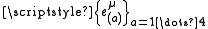
that together span the 4D vector tangent space
at each point in spacetime
. Here, spacetime means a four-dimensional, smooth, connected Lorentzian manifold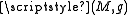
. All tensors of the theory are then expressed in this vector basis, by projecting them against members of the tetrad. For example, the spacetime metric itself can be transformed from a coordinate basis to the tetrad basis:
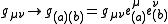
Popular tetrad bases include orthonormal tetrads and null tetrads. The latter are used frequently in problems dealing with radiation, and are the basis of the Newman-Penrose formalism
.
From a mathematical point of view, the four vector fields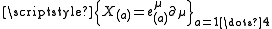
define a parallelization
of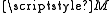
. Hence—in this case—the tangent bundle
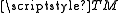is diffeomorphic to the product manifolds 
.
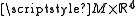The coordinate tetrad is commonly denoted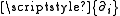
. These tangent vectors
are usually defined as directional derivative
operators; given a chart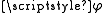
(which maps a subset of the manifold
into coordinate space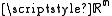
) and any scalar field
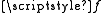, the coordinate vectors are such that: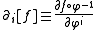
Any tensor
can be written in terms of this tetrad (and its dual vector counterparts, which are defined such that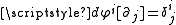
using the Kronecker delta). For example, the metric tensor
can be expressed: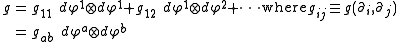
The involvement of the coordinate tetrad is not normally made explicit. Instead of writing tensor equations out fully (including tetrad elements and tensor products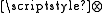
as above) only components of the tensors are mentioned. For example, the metric is written as "
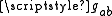". This is called abstract index notation
.
Changing tetrad is a routine operation in the standard formalism, as it is involved in every coordinate transformation (i.e., changing from one coordinate tetrad basis to another). Switching between multiple coordinate charts is necessary because, except in trivial cases, it is not possible for a single coordinate chart to cover the entire manifold.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
In the tetrad formalism all tensors are represented in terms of a chosen basis, a set of four vector
Vector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
s called the tetrad. (When applied to theories with other than four dimensions, this approach is given other names; see also Cartan formalism). As a formalism
Formalism (mathematics)
In foundations of mathematics, philosophy of mathematics, and philosophy of logic, formalism is a theory that holds that statements of mathematics and logic can be thought of as statements about the consequences of certain string manipulation rules....
rather than a separate theory, it does not make different predictions but does allow the relevant equations to be expressed differently.
The advantage of the tetrad formalism over the standard coordinate-based approach to GR lies in the ability to choose the tetrad basis to reflect important physical aspects of the spacetime.
Mathematical details
In the tetrad formalism, a tetrad basis is chosen — a set of four independent vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s
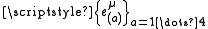that together span the 4D vector tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at each point in spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. Here, spacetime means a four-dimensional, smooth, connected Lorentzian manifold
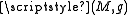. All tensors of the theory are then expressed in this vector basis, by projecting them against members of the tetrad. For example, the spacetime metric itself can be transformed from a coordinate basis to the tetrad basis: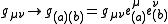Popular tetrad bases include orthonormal tetrads and null tetrads. The latter are used frequently in problems dealing with radiation, and are the basis of the Newman-Penrose formalism
Newman-Penrose Formalism
The Newman-Penrose Formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for General Relativity. Their notation is an effort to treat General Relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR.The NP formalism is itself a...
.
From a mathematical point of view, the four vector fields
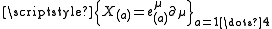define a parallelizationParallelization (mathematics)
In mathematics, a parallelization of a manifold M\, of dimension n is a set of n global linearly independent vector fields.-Formal definition:...
of
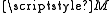. Hence—in this case—the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
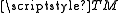is diffeomorphic to the product manifolds 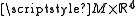.Relation to standard formalism
The standard formalism of differential geometry (and General Relativity) consists simply of using the coordinate tetrad in the tetrad formalism. The coordinate tetrad is the canonical set of vectors associated with the coordinate chart.The coordinate tetrad is commonly denoted
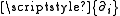. These tangent vectorsTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
are usually defined as directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
operators; given a chart
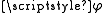(which maps a subset of the manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
into coordinate space
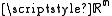) and any scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
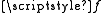, the coordinate vectors are such that: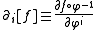Any tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
can be written in terms of this tetrad (and its dual vector counterparts, which are defined such that
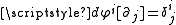using the Kronecker delta). For example, the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
can be expressed:
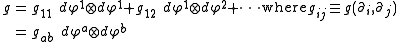
The involvement of the coordinate tetrad is not normally made explicit. Instead of writing tensor equations out fully (including tetrad elements and tensor products
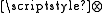as above) only components of the tensors are mentioned. For example, the metric is written as "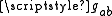". This is called abstract index notationAbstract index notation
Abstract index notation is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeholders, not related to any fixed basis and, in particular, are non-numerical...
.
Changing tetrad is a routine operation in the standard formalism, as it is involved in every coordinate transformation (i.e., changing from one coordinate tetrad basis to another). Switching between multiple coordinate charts is necessary because, except in trivial cases, it is not possible for a single coordinate chart to cover the entire manifold.
See also
- Frame bundleFrame bundleIn mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
- Orthonormal frame bundle
- Principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
- Spin bundle
- Connection (mathematics)Connection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
- G-structureG-structureIn differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
- Spin manifold
- Spin structureSpin structureIn differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....