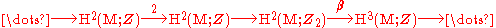Spin structure
Encyclopedia
In differential geometry, a spin structure on an orientable Riemannian manifold
allows one to define associated spinor bundles, giving rise to the notion of a spinor
in differential geometry.
Spin structures have wide applications to mathematical physics
, in particular to quantum field theory
where they are an essential ingredient in the definition of any theory with uncharged fermions. They are also of purely mathematical interest in differential geometry, algebraic topology
, and K theory. They form the foundation for spin geometry
.
, as well as in field theory
, given an oriented Riemannian manifold one wishes that it admits spinor
one wishes that it admits spinor
s. A method for dealing with this problem is to require that has a spin structure. There is a topological obstruction to the existence of spin structures on a Riemannian manifold
has a spin structure. There is a topological obstruction to the existence of spin structures on a Riemannian manifold  . Such structures will exist if and only if the second Stiefel-Whitney class
. Such structures will exist if and only if the second Stiefel-Whitney class 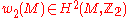 of
of  vanishes. Furthermore, if
vanishes. Furthermore, if 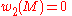 , then the set of the isomorphism classes of spin structures on
, then the set of the isomorphism classes of spin structures on  is acted upon freely and transitively by
is acted upon freely and transitively by  . As the manifold
. As the manifold  is assumed to be oriented, the first Stiefel-Whitney class
is assumed to be oriented, the first Stiefel-Whitney class 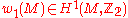 of
of  vanishes too.
vanishes too.
(The Stiefel-Whitney classes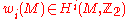 of a manifold
of a manifold  are defined to be the Stiefel-Whitney classes of its tangent bundle
are defined to be the Stiefel-Whitney classes of its tangent bundle
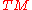 .)
.)
The bundle of spinors over
over  is then the complex vector bundle associated to the corresponding principal bundle
is then the complex vector bundle associated to the corresponding principal bundle
 of spin frames over
of spin frames over  and the spin representation of its structure group
and the spin representation of its structure group  on the space of spinors
on the space of spinors 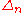 . The bundle
. The bundle 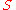 is called the spinor bundle for a given spin structure on
is called the spinor bundle for a given spin structure on  .
.
A precise definition of spin structure on manifold was possible only after the notion of fiber bundle
had been introduced; André Haefliger
(1956) found the topological obstruction to the existence of a spin structure on an orientable Riemannian manifold and Max Karoubi
(1968) extended this result to the non-orientable pseudo-Riemannian case.
 is an equivariant
is an equivariant
lift of the oriented orthonormal frame bundle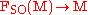 with respect to the double covering
with respect to the double covering  . In other words, a pair
. In other words, a pair 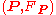 is a spin structure on the principal bundle
is a spin structure on the principal bundle 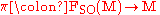 when
when
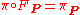 and
and 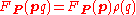 for all
for all 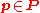 and
and 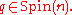
The principal bundle is also called the bundle of spin frames over
is also called the bundle of spin frames over  .
.
Two spin structures and
and  on the same oriented Riemannian manifold
on the same oriented Riemannian manifold
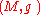 are called equivalent if there exists a
are called equivalent if there exists a  -equivariant map
-equivariant map 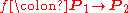 such that
such that
 and
and 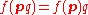 for all
for all 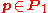 and
and 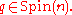
Of course, in this case and
and  are two equivalent double coverings of the oriented orthonormal frame
are two equivalent double coverings of the oriented orthonormal frame  -bundle
-bundle 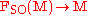 of the given Riemannian manifold
of the given Riemannian manifold 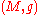 .
.
This definition of spin structure on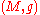 as a spin structure on the principal bundle
as a spin structure on the principal bundle 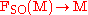 is due to André Haefliger
is due to André Haefliger
(1956).
found necessary and sufficient conditions for the existence of a spin structure on an oriented Riemannian manifold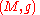 . The obstruction to having a spin structure is certain element
. The obstruction to having a spin structure is certain element  of
of  . For a spin structure the class
. For a spin structure the class  is the second Stiefel-Whitney class
is the second Stiefel-Whitney class 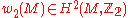 of
of  . Hence, a spin structure exists if and only if the second Stiefel-Whitney class
. Hence, a spin structure exists if and only if the second Stiefel-Whitney class 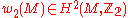 of
of  vanishes.
vanishes.
and E an oriented vector bundle on M of dimension n equipped with a fibre metric. This means that at each point of M, the fibre of E is an inner product space
. A spinor bundle of E is a prescription for consistently associating a spin representation to every point of M. There are topological obstructions to being able to do it, and consequently, a given bundle E may not admit any spinor bundle. In case it does, one says that the bundle E is spin.
This may be made rigorous through the language of principal bundle
s. The collection of oriented orthonormal frame
s of a vector bundle form a frame bundle
PSO(E), which is a principal bundle under the action of the special orthogonal group SO(n). A spin structure for PSO(E) is a lift of PSO(E) to a principal bundle PSpin(E) under the action of the spin group Spin(n), by which we mean that there exists a bundle map φ : PSpin(E) → PSO(E) such that , for all p ∈ PSpin(E) and g ∈ Spin(n),
, for all p ∈ PSpin(E) and g ∈ Spin(n),
where is the mapping of groups presenting the spin group as a double-cover of SO(n).
is the mapping of groups presenting the spin group as a double-cover of SO(n).
In the special case in which E is the tangent bundle
 over the base manifold
over the base manifold  , if a spin structure exists then one says that M is a spin manifold. Equivalently M is spin if the SO(n) principal bundle of orthonormal bases
, if a spin structure exists then one says that M is a spin manifold. Equivalently M is spin if the SO(n) principal bundle of orthonormal bases
of the tangent fibers of M is a Z2 quotient of a principal spin bundle.
If the manifold has a cell decomposition
or a triangulation
, a spin structure can equivalently be thought of as a homotopy-class of trivialization of the tangent bundle
over the 1-skeleton
that extends over the 2-skeleton. If the dimension is lower than 3, one first takes a Whitney sum with a trivial line bundle.
and Friedrich Hirzebruch
. Note, we have assumed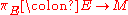 is an orientable vector bundle
is an orientable vector bundle
.
is isomorphic to H1(M,Z2). More precisely, the space of the isomorphism classes of spin structures is an affine space
over H1(M,Z2).
Intuitively, for each nontrivial cycle on M a spin structure corresponds to a binary choice of whether a section of the SO(N) bundle switches sheets when one encircles the loop. If w2 vanishes then these choices may be extended over the two-skeleton, then (by obstruction theory
) they may automatically be extended over all of M. In particle physics
this corresponds to a choice of periodic or antiperiodic boundary conditions for fermions going around each loop.
the spin statistics theorem implies that the wavefunction
of an uncharged fermion
is a section of the associated vector bundle to the spin lift of an SO(N) bundle E. Therefore the choice of spin structure is part of the data needed to define the wavefunction, and one often needs to sum over these choices in the partition function
. In many physical theories E is the tangent bundle
, but for the fermions on the worldvolumes of D-branes in string theory
it is a normal bundle
.
, but uses the spinc group, which is defined instead by the exact sequence

To motivate this, suppose that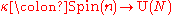 is a complex spinor representation. The center of
is a complex spinor representation. The center of 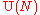 consists of the diagonal elements coming from the inclusion
consists of the diagonal elements coming from the inclusion 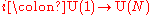 , i.e., the scalar multiples of the identity. Thus there is a homomorphism
, i.e., the scalar multiples of the identity. Thus there is a homomorphism
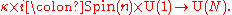
This will always have the element (-1,-1) in the kernel. Taking the quotient modulo this element gives the group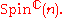 This is the twisted product
This is the twisted product
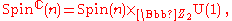
where . In other words, the group Spinc(n) is a central extension of SO(n) by S1.
. In other words, the group Spinc(n) is a central extension of SO(n) by S1.
Viewed another way, Spinc(n) is the quotient group obtained from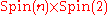 with respect to the normal
with respect to the normal 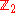 which is generated by the pair of covering transformations for the bundles
which is generated by the pair of covering transformations for the bundles  and
and  respectively. This makes the spinc group both a bundle over the circle with fibre
respectively. This makes the spinc group both a bundle over the circle with fibre  , and a bundle over
, and a bundle over  with fibre a circle.
with fibre a circle.
The fundamental group is isomorphic to
is isomorphic to 
If the manifold has a cell decomposition
or a triangulation
, a spinc structure can be equivalently thought of as a homotopy class of complex structure over the 2-skeleton
that extends over the 3-skeleton. Similarly to the case of spin structures, one takes a Whitney sum with a trivial line bundle if the manifold is odd dimensional.
Yet another definition is that a spinc structure on a manifold is a complex line bundle
is a complex line bundle 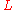 over
over  together with a spin structure on
together with a spin structure on  .
.
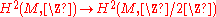 (in other words, the third integral Stiefel-Whitney class vanishes). In this case one says that E is spinc. Intuitively, the lift gives the Chern class
(in other words, the third integral Stiefel-Whitney class vanishes). In this case one says that E is spinc. Intuitively, the lift gives the Chern class
of the square of the U(1) part of any obtained spinc bundle.
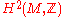 . Thus, spinc-structures correspond to elements of
. Thus, spinc-structures correspond to elements of 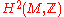 although not in a natural way.
although not in a natural way.
. When the spinc structure is nonzero this square root bundle has a non-integral Chern class, which means that it fails the triple overlap condition. In particular, the product of transition functions on a three-way intersection is not always equal to one, as is required for a principal bundle
. Instead it is sometimes −1.
This failure occurs at precisely the same intersections as an identical failure in the triple products of transition functions of the obstructed spin bundle. Therefore the triple products of transition functions of the full spinc bundle, which are the products of the triple product of the spin and U(1) component bundles, are either 12=1 or -12=1 and so the spinc bundle satisfies the triple overlap condition and is therefore a legitimate bundle.
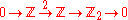 where the second arrow
where the second arrow
is multiplication
by 2 and the third is reduction modulo 2. This induces a long exact sequence on cohomology, which contains
where the second arrow
is induced by multiplication by 2, the third is induced by restriction modulo 2 and the fourth is the associated Bockstein homomorphism
β.
The obstruction to the existence of a spin bundle is an element w2 of H2(M,Z2). It reflects the fact that one may always locally lift an SO(N) bundle to a spin bundle, but one needs to choose a Z2 lift of each transition function, which is a choice of sign. The lift does not exist when the product of these three signs on a triple overlap is -1, which yields the Čech cohomology
picture of w2.
To cancel this obstruction, one tensors this spin bundle with a U(1) bundle with the same obstruction w2. Notice that this is an abuse of the word bundle, as neither the spin bundle nor the U(1) bundle satisfies the triple overlap condition and so neither is actually a bundle.
A legitimate U(1) bundle is classified by its Chern class
, which is an element of H2(M,Z).
Identify this class with the first element in the above exact sequence. The next arrow doubles this Chern class, and so legitimate bundles will correspond to even elements in the second H2(M,Z), while odd elements will correspond to bundles that fail the triple overlap condition. The obstruction then is classified by the failure of an element in the second H2(M,Z) to be in the image of the arrow, which, by exactness, is classified by its image in H2(M,Z2) under the next arrow.
To cancel the corresponding obstruction in the spin bundle, this image needs to be w2. In particular, if w2 is not in the image of the arrow, then there does not exist any U(1) bundle with obstruction equal to w2 and so the obstruction cannot be cancelled. By exactness, w2 is in the image of the preceding arrow only if it is in the kernel of the next arrow, which we recall is the Bockstein homomorphism
β. That is, the condition for the cancellation of the obstruction is
where we have used the fact that the third integral Stiefel-Whitney class W3 is the Bockstein of the second Stiefel-Whitney class w2 (this can be taken as a definition of W3).
degree, which are called the integral Stiefel-Whitney classes, and are labeled by their degree (which is always odd).
charged spinors are sections of associated spinc bundles, and in particular no charged spinors can exist on a space that is not spinc. An exception arises in some supergravity
theories where additional interactions imply that other fields may cancel the third Stiefel-Whitney class.
s to associated spin bundles, vector structures are lifts of other bundles to associated vector bundles.
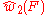 .
.
, Joseph Polchinski
, John Schwarz, Nathan Seiberg
and Edward Witten
. They were considering type I string theory
, whose configurations consist of a 10-manifold with a Spin(32)/Z2 principle bundle over it. Such a bundle has a vector structure, and so lifts to an SO(32) bundle, when the triple product of the transition functions on all triple intersection is the trivial element of the Z2 quotient. This happens precisely when , the characteristic 2-cocycle with Z2 coefficients, vanishes.
, the characteristic 2-cocycle with Z2 coefficients, vanishes.
The following year, in
The Mirror Transform of Type I Vacua in Six Dimensions, Ashoke Sen
and Savdeep Sethi demonstrated that type I superstring theory is only consistent, in the absence of fluxes, when this characteristic class is trivial. More generally, in type I string theory the B-field is also a class in the second cohomology with Z2 coefficients and they demonstrated that it must be equal to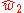 .
.
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
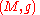
allows one to define associated spinor bundles, giving rise to the notion of a spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
in differential geometry.
Spin structures have wide applications to mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, in particular to quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
where they are an essential ingredient in the definition of any theory with uncharged fermions. They are also of purely mathematical interest in differential geometry, algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, and K theory. They form the foundation for spin geometry
Spin geometry
Spin geometry is the area of differential geometry and topology where objects like spin manifoldsand Dirac operators, and the various associated index theorems have come to play a fundamental role both in mathematics and in mathematical physics....
.
Introduction
In geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, as well as in field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, given an oriented Riemannian manifold
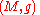 one wishes that it admits spinor
one wishes that it admits spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s. A method for dealing with this problem is to require that
 has a spin structure. There is a topological obstruction to the existence of spin structures on a Riemannian manifold
has a spin structure. There is a topological obstruction to the existence of spin structures on a Riemannian manifold 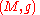 . Such structures will exist if and only if the second Stiefel-Whitney class
. Such structures will exist if and only if the second Stiefel-Whitney class 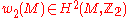 of
of  vanishes. Furthermore, if
vanishes. Furthermore, if 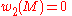 , then the set of the isomorphism classes of spin structures on
, then the set of the isomorphism classes of spin structures on  is acted upon freely and transitively by
is acted upon freely and transitively by  . As the manifold
. As the manifold  is assumed to be oriented, the first Stiefel-Whitney class
is assumed to be oriented, the first Stiefel-Whitney class 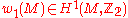 of
of  vanishes too.
vanishes too.(The Stiefel-Whitney classes
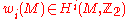 of a manifold
of a manifold  are defined to be the Stiefel-Whitney classes of its tangent bundle
are defined to be the Stiefel-Whitney classes of its tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
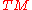 .)
.)The bundle of spinors
 over
over  is then the complex vector bundle associated to the corresponding principal bundle
is then the complex vector bundle associated to the corresponding principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
 of spin frames over
of spin frames over  and the spin representation of its structure group
and the spin representation of its structure group  on the space of spinors
on the space of spinors 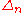 . The bundle
. The bundle 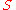 is called the spinor bundle for a given spin structure on
is called the spinor bundle for a given spin structure on  .
.A precise definition of spin structure on manifold was possible only after the notion of fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
had been introduced; André Haefliger
André Haefliger
André Haefliger is a Swiss mathematician who works primarily on topology.He studied mathematics in Lausanne. He received his PhD in 1958 from the University of Strasbourg under the supervision of Charles Ehresmann with "Structures feuilletées et cohomologie à valeurs dans un faisceau de...
(1956) found the topological obstruction to the existence of a spin structure on an orientable Riemannian manifold and Max Karoubi
Max Karoubi
Max Karoubi is French a mathematician who works on K-theory and who founded the European mathematical society. He was one of Henri Cartan's students.-References:* of Max Karoubi* in nlab...
(1968) extended this result to the non-orientable pseudo-Riemannian case.
Definition
A spin structure on an orientable Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
 is an equivariant
is an equivariantEquivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
lift of the oriented orthonormal frame bundle
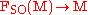 with respect to the double covering
with respect to the double covering  . In other words, a pair
. In other words, a pair 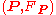 is a spin structure on the principal bundle
is a spin structure on the principal bundle 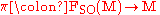 when
when
- a)
 is a principal
is a principal  -bundle over
-bundle over  ,
, - b)
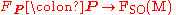 is an equivariantEquivariantIn mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
is an equivariantEquivariantIn mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
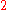 -fold covering mapCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
-fold covering mapCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
such that
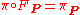 and
and 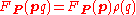 for all
for all 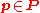 and
and 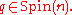
The principal bundle
 is also called the bundle of spin frames over
is also called the bundle of spin frames over  .
.Two spin structures
 and
and  on the same oriented Riemannian manifold
on the same oriented Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
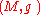 are called equivalent if there exists a
are called equivalent if there exists a  -equivariant map
-equivariant map 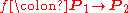 such that
such that and
and 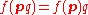 for all
for all 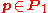 and
and 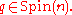
Of course, in this case
 and
and  are two equivalent double coverings of the oriented orthonormal frame
are two equivalent double coverings of the oriented orthonormal frame  -bundle
-bundle 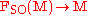 of the given Riemannian manifold
of the given Riemannian manifold 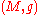 .
.This definition of spin structure on
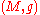 as a spin structure on the principal bundle
as a spin structure on the principal bundle 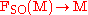 is due to André Haefliger
is due to André HaefligerAndré Haefliger
André Haefliger is a Swiss mathematician who works primarily on topology.He studied mathematics in Lausanne. He received his PhD in 1958 from the University of Strasbourg under the supervision of Charles Ehresmann with "Structures feuilletées et cohomologie à valeurs dans un faisceau de...
(1956).
Obstruction
André HaefligerAndré Haefliger
André Haefliger is a Swiss mathematician who works primarily on topology.He studied mathematics in Lausanne. He received his PhD in 1958 from the University of Strasbourg under the supervision of Charles Ehresmann with "Structures feuilletées et cohomologie à valeurs dans un faisceau de...
found necessary and sufficient conditions for the existence of a spin structure on an oriented Riemannian manifold
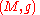 . The obstruction to having a spin structure is certain element
. The obstruction to having a spin structure is certain element  of
of  . For a spin structure the class
. For a spin structure the class  is the second Stiefel-Whitney class
is the second Stiefel-Whitney class 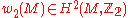 of
of  . Hence, a spin structure exists if and only if the second Stiefel-Whitney class
. Hence, a spin structure exists if and only if the second Stiefel-Whitney class 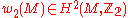 of
of  vanishes.
vanishes.Spin structures on vector bundles
Let M be a paracompact topological manifoldTopological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
and E an oriented vector bundle on M of dimension n equipped with a fibre metric. This means that at each point of M, the fibre of E is an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
. A spinor bundle of E is a prescription for consistently associating a spin representation to every point of M. There are topological obstructions to being able to do it, and consequently, a given bundle E may not admit any spinor bundle. In case it does, one says that the bundle E is spin.
This may be made rigorous through the language of principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s. The collection of oriented orthonormal frame
Orthonormal frame
In Riemannian geometry and relativity theory, an orthonormal frame is a tool for studying the structure of a differentiable manifold equipped with a metric...
s of a vector bundle form a frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
PSO(E), which is a principal bundle under the action of the special orthogonal group SO(n). A spin structure for PSO(E) is a lift of PSO(E) to a principal bundle PSpin(E) under the action of the spin group Spin(n), by which we mean that there exists a bundle map φ : PSpin(E) → PSO(E) such that
 , for all p ∈ PSpin(E) and g ∈ Spin(n),
, for all p ∈ PSpin(E) and g ∈ Spin(n),where
 is the mapping of groups presenting the spin group as a double-cover of SO(n).
is the mapping of groups presenting the spin group as a double-cover of SO(n).In the special case in which E is the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
 over the base manifold
over the base manifold  , if a spin structure exists then one says that M is a spin manifold. Equivalently M is spin if the SO(n) principal bundle of orthonormal bases
, if a spin structure exists then one says that M is a spin manifold. Equivalently M is spin if the SO(n) principal bundle of orthonormal basesOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of the tangent fibers of M is a Z2 quotient of a principal spin bundle.
If the manifold has a cell decomposition
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
or a triangulation
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
, a spin structure can equivalently be thought of as a homotopy-class of trivialization of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
over the 1-skeleton
Skeleton
The skeleton is the body part that forms the supporting structure of an organism. There are two different skeletal types: the exoskeleton, which is the stable outer shell of an organism, and the endoskeleton, which forms the support structure inside the body.In a figurative sense, skeleton can...
that extends over the 2-skeleton. If the dimension is lower than 3, one first takes a Whitney sum with a trivial line bundle.
Obstruction
A spin structure on a vector bunddle E exists if and only if the second Stiefel-Whitney class w2 of E vanishes. This is a result of Armand BorelArmand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
and Friedrich Hirzebruch
Friedrich Hirzebruch
Friedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
. Note, we have assumed
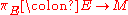 is an orientable vector bundle
is an orientable vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
.
Classification
When spin structures exist, the inequivalent spin structures on a manifold have a one-to-one correspondence (not canonical) with the elements of H1(M,Z2), which by the universal coefficient theoremUniversal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
is isomorphic to H1(M,Z2). More precisely, the space of the isomorphism classes of spin structures is an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
over H1(M,Z2).
Intuitively, for each nontrivial cycle on M a spin structure corresponds to a binary choice of whether a section of the SO(N) bundle switches sheets when one encircles the loop. If w2 vanishes then these choices may be extended over the two-skeleton, then (by obstruction theory
Obstruction theory
In mathematics, obstruction theory is a name given to two different mathematical theories, both of which yield cohomological invariants.-In homotopy theory:...
) they may automatically be extended over all of M. In particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
this corresponds to a choice of periodic or antiperiodic boundary conditions for fermions going around each loop.
Application to particle physics
In particle physicsParticle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
the spin statistics theorem implies that the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of an uncharged fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
is a section of the associated vector bundle to the spin lift of an SO(N) bundle E. Therefore the choice of spin structure is part of the data needed to define the wavefunction, and one often needs to sum over these choices in the partition function
Partition function (quantum field theory)
In quantum field theory, we have a generating functional, Z[J] of correlation functions and this value, called the partition function is usually expressed by something like the following functional integral:...
. In many physical theories E is the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, but for the fermions on the worldvolumes of D-branes in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
it is a normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
.
Examples
- A genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
g Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
admits 22g inequivalent spin structures; see theta characteristicTheta characteristicIn mathematics, a theta characteristic of a non-singular algebraic curve C is a divisor class Θ such that 2Θ is the canonical class, In terms of holomorphic line bundles L on a connected compact Riemann surface, it is therefore L such that L2 is the canonical bundle, here also equivalently the...
. - The complex projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
CP2 is not spin. - All even dimensional complex projective spaceComplex projective spaceIn mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
s CP2n are not spin - All odd dimensional complex projective spaceComplex projective spaceIn mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
s CP2n+1 are spin - All compact, orientable manifolds of dimension 3 or less are spin.
- All Calabi-Yau manifoldCalabi-Yau manifoldA Calabi-Yau manifold is a special type of manifold that shows up in certain branches of mathematics such as algebraic geometry, as well as in theoretical physics...
s are spin.
Properties
- The  genus of a spin manifold is an integer, and is an even integer if in addition the dimension is 4 mod 8.
- In general the  genus is a rational invariant, defined for any manifold, but it is not in general an integer.
- This was originally proven by HirzebruchFriedrich HirzebruchFriedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
and BorelArmand BorelArmand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
, and can be proven by the Atiyah–Singer index theoremAtiyah–Singer index theoremIn differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
, by realizing the  genus as the index of a Dirac operatorDirac operatorIn mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
– a Dirac operator is a square root of a second order operator, and exists due to the spin structure being a "square root". This was a motivating example for the index theorem.
Spinc structures
A spinc structure is analogous to a spin structure on an oriented Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, but uses the spinc group, which is defined instead by the exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...

To motivate this, suppose that
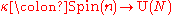 is a complex spinor representation. The center of
is a complex spinor representation. The center of 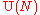 consists of the diagonal elements coming from the inclusion
consists of the diagonal elements coming from the inclusion 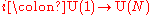 , i.e., the scalar multiples of the identity. Thus there is a homomorphism
, i.e., the scalar multiples of the identity. Thus there is a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
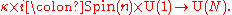
This will always have the element (-1,-1) in the kernel. Taking the quotient modulo this element gives the group
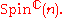 This is the twisted product
This is the twisted product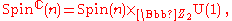
where
 . In other words, the group Spinc(n) is a central extension of SO(n) by S1.
. In other words, the group Spinc(n) is a central extension of SO(n) by S1.Viewed another way, Spinc(n) is the quotient group obtained from
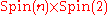 with respect to the normal
with respect to the normal 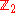 which is generated by the pair of covering transformations for the bundles
which is generated by the pair of covering transformations for the bundles  and
and  respectively. This makes the spinc group both a bundle over the circle with fibre
respectively. This makes the spinc group both a bundle over the circle with fibre  , and a bundle over
, and a bundle over  with fibre a circle.
with fibre a circle.The fundamental group
 is isomorphic to
is isomorphic to 
If the manifold has a cell decomposition
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
or a triangulation
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
, a spinc structure can be equivalently thought of as a homotopy class of complex structure over the 2-skeleton
Skeleton
The skeleton is the body part that forms the supporting structure of an organism. There are two different skeletal types: the exoskeleton, which is the stable outer shell of an organism, and the endoskeleton, which forms the support structure inside the body.In a figurative sense, skeleton can...
that extends over the 3-skeleton. Similarly to the case of spin structures, one takes a Whitney sum with a trivial line bundle if the manifold is odd dimensional.
Yet another definition is that a spinc structure on a manifold
 is a complex line bundle
is a complex line bundle 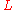 over
over  together with a spin structure on
together with a spin structure on  .
.Obstruction
A spinc structure exists when the bundle is orientable and the second Stiefel-Whitney class of the bundle E is in the image of the map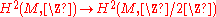 (in other words, the third integral Stiefel-Whitney class vanishes). In this case one says that E is spinc. Intuitively, the lift gives the Chern class
(in other words, the third integral Stiefel-Whitney class vanishes). In this case one says that E is spinc. Intuitively, the lift gives the Chern classChern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the square of the U(1) part of any obtained spinc bundle.
Classification
When a manifold carries a spinc structure at all, the set of spinc structures forms an affine space. Moreover, the set of spinc structures has a free transitive action of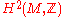 . Thus, spinc-structures correspond to elements of
. Thus, spinc-structures correspond to elements of 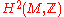 although not in a natural way.
although not in a natural way.Geometric picture
This has the following geometric interpretation, which is due to Edward WittenEdward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
. When the spinc structure is nonzero this square root bundle has a non-integral Chern class, which means that it fails the triple overlap condition. In particular, the product of transition functions on a three-way intersection is not always equal to one, as is required for a principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
. Instead it is sometimes −1.
This failure occurs at precisely the same intersections as an identical failure in the triple products of transition functions of the obstructed spin bundle. Therefore the triple products of transition functions of the full spinc bundle, which are the products of the triple product of the spin and U(1) component bundles, are either 12=1 or -12=1 and so the spinc bundle satisfies the triple overlap condition and is therefore a legitimate bundle.
The details
The above intuitive geometric picture may be made concrete as follows. Consider the short exact sequence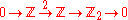 where the second arrow
where the second arrowArrow
An arrow is a shafted projectile that is shot with a bow. It predates recorded history and is common to most cultures.An arrow usually consists of a shaft with an arrowhead attached to the front end, with fletchings and a nock at the other.- History:...
is multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
by 2 and the third is reduction modulo 2. This induces a long exact sequence on cohomology, which contains
where the second arrow
Arrow
An arrow is a shafted projectile that is shot with a bow. It predates recorded history and is common to most cultures.An arrow usually consists of a shaft with an arrowhead attached to the front end, with fletchings and a nock at the other.- History:...
is induced by multiplication by 2, the third is induced by restriction modulo 2 and the fourth is the associated Bockstein homomorphism
Bockstein homomorphism
In homological algebra, the Bockstein homomorphism, introduced by , is a connecting homomorphism associated with a short exact sequenceof abelian groups, when they are introduced as coefficients into a chain complex C, and which appears in the homology groups as a homomorphism reducing degree by...
β.
The obstruction to the existence of a spin bundle is an element w2 of H2(M,Z2). It reflects the fact that one may always locally lift an SO(N) bundle to a spin bundle, but one needs to choose a Z2 lift of each transition function, which is a choice of sign. The lift does not exist when the product of these three signs on a triple overlap is -1, which yields the Čech cohomology
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
picture of w2.
To cancel this obstruction, one tensors this spin bundle with a U(1) bundle with the same obstruction w2. Notice that this is an abuse of the word bundle, as neither the spin bundle nor the U(1) bundle satisfies the triple overlap condition and so neither is actually a bundle.
A legitimate U(1) bundle is classified by its Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
, which is an element of H2(M,Z).
Identify this class with the first element in the above exact sequence. The next arrow doubles this Chern class, and so legitimate bundles will correspond to even elements in the second H2(M,Z), while odd elements will correspond to bundles that fail the triple overlap condition. The obstruction then is classified by the failure of an element in the second H2(M,Z) to be in the image of the arrow, which, by exactness, is classified by its image in H2(M,Z2) under the next arrow.
To cancel the corresponding obstruction in the spin bundle, this image needs to be w2. In particular, if w2 is not in the image of the arrow, then there does not exist any U(1) bundle with obstruction equal to w2 and so the obstruction cannot be cancelled. By exactness, w2 is in the image of the preceding arrow only if it is in the kernel of the next arrow, which we recall is the Bockstein homomorphism
Bockstein homomorphism
In homological algebra, the Bockstein homomorphism, introduced by , is a connecting homomorphism associated with a short exact sequenceof abelian groups, when they are introduced as coefficients into a chain complex C, and which appears in the homology groups as a homomorphism reducing degree by...
β. That is, the condition for the cancellation of the obstruction is
where we have used the fact that the third integral Stiefel-Whitney class W3 is the Bockstein of the second Stiefel-Whitney class w2 (this can be taken as a definition of W3).
Integral lifts of Stiefel-Whitney classes
This argument also demonstrates that second Stiefel-Whitney class defines elements not only of Z2 cohomology but also of integral cohomology in one higher degree. In fact this is the case for all even Stiefel-Whitney classes. It is traditional to use an uppercase W for the resulting classes in odddegree, which are called the integral Stiefel-Whitney classes, and are labeled by their degree (which is always odd).
Application to particle physics
In quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
charged spinors are sections of associated spinc bundles, and in particular no charged spinors can exist on a space that is not spinc. An exception arises in some supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
theories where additional interactions imply that other fields may cancel the third Stiefel-Whitney class.
Examples
- All oriented smooth manifolds of dimension 4 or less are spinc.
- All almost complex manifoldAlmost complex manifoldIn mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
s are spinc. - All spin manifolds are spinc.
Vector structures
While spin structures are lifts of vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s to associated spin bundles, vector structures are lifts of other bundles to associated vector bundles.
Obstruction
For example, consider an SO(8) bundle. The group SO(8) has three 8-dimensional representations, two of which are spinorial and one of which is the vector representation. These three representations are exchanged by an isomorphism known as triality. Given an SO(8) vector bundle E, the obstruction to the construction of an associated spin bundle is the second Stiefel-Whitney class w2(E), which is an element of the second cohomology group with Z2 coefficients. By triality, given an SO(8) spin bundle F, the obstruction to the existence of an associated vector bundle is another element of the same cohomology group, which is often denoted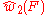 .
.Application to particle physics
Vector structures were first considered in physics, in the paper Anomalies, Dualities and Topology of D=6, N=1 Superstring Vacua by Micha Berkooz, Robert LeighRobert Leigh
Robert Leigh is a physicist working on string theory.He obtained his B.Sc. degree from the University of Guelph in 1986, and his Ph.D. from the University of Texas at Austin in 1991, working with Joe Polchinski...
, Joseph Polchinski
Joseph Polchinski
Joseph Polchinski is a physicist working on string theory. He graduated from Canyon del Oro High School in Tucson, Arizona in 1971, obtained his B.S. degree from Caltech in 1975, and his Ph.D. from the University of California, Berkeley in 1980 under the supervision of Stanley Mandelstam...
, John Schwarz, Nathan Seiberg
Nathan Seiberg
Nathan "Nati" Seiberg is an Israeli American theoretical physicist who works on string theory. He was recipient of a 1996 MacArthur Fellowship and the Dannie Heineman Prize for Mathematical Physics in 1998. He is currently a professor at the Institute for Advanced Study in Princeton, New Jersey, USA...
and Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
. They were considering type I string theory
Type I string theory
In theoretical physics, type I string theory is one of five consistent supersymmetric string theories in ten dimensions. It is the only one whose strings are unoriented and which contains not only closed strings, but also open strings.The classic 1976 work of Ferdinando Gliozzi, Joel Scherk and...
, whose configurations consist of a 10-manifold with a Spin(32)/Z2 principle bundle over it. Such a bundle has a vector structure, and so lifts to an SO(32) bundle, when the triple product of the transition functions on all triple intersection is the trivial element of the Z2 quotient. This happens precisely when
 , the characteristic 2-cocycle with Z2 coefficients, vanishes.
, the characteristic 2-cocycle with Z2 coefficients, vanishes.The following year, in
The Mirror Transform of Type I Vacua in Six Dimensions, Ashoke Sen
Ashoke Sen
Ashoke Sen , FRS, is an Indian theoretical physicist. He has made a number of major original contributions to the subject of string theory, including his landmark paper on strong-weak coupling duality or S-duality, which was influential in changing the course of research in the field...
and Savdeep Sethi demonstrated that type I superstring theory is only consistent, in the absence of fluxes, when this characteristic class is trivial. More generally, in type I string theory the B-field is also a class in the second cohomology with Z2 coefficients and they demonstrated that it must be equal to
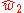 .
.Further reading
- Something on Spin Structures by Sven-S. Porst is a short introduction to orientationOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
and spin structures for mathematics students.