T-norm
Encyclopedia
In mathematics
, a t-norm (also T-norm or, unabbreviated, triangular norm) is a kind of binary operation
used in the framework of probabilistic metric space
s and in multi-valued logic
, specifically in fuzzy logic
. A t-norm generalizes intersection
in a lattice
and conjunction
in logic
. The name triangular norm refers to the fact that in the framework of probabilistic metric spaces t-norms are used to generalize triangle inequality
of ordinary metric space
s.
T: [0, 1] × [0, 1] → [0, 1] which satisfies the following properties:
Since a t-norm is a binary algebraic operation
on the interval [0, 1], infix algebraic notation is also common, with the t-norm usually denoted by .
.
The defining conditions of the t-norm are exactly those of the partially ordered Abelian monoid on the real unit interval [0, 1]. (Cf. ordered group
.) The monoidal operation of any partially ordered Abelian monoid L is therefore by some authors called a triangular norm on L.
, studied by classical logic, for fuzzy logic
s. Indeed, the classical Boolean conjunction is both commutative and associative. The monotonicity property ensures that the degree of truth of conjunction does not decrease if the truth values of conjuncts increase. The requirement that 1 be an identity element corresponds to the interpretation of 1 as true (and consequently 0 as false). Continuity, which is often required from fuzzy conjunction as well, expresses the idea that, roughly speaking, very small changes in truth values of conjuncts should not macroscopically affect the truth value of their conjunction.
T-norms are also used to construct the intersection
of fuzzy set
s or as a basis for aggregation operators (see fuzzy set operations
). In probabilistic metric space
s, t-norms are used to generalize triangle inequality
of ordinary metric spaces. Individual t-norms may of course frequently occur in further disciplines of mathematics, since the class contains many familiar functions.
as a function, in the usual interval topology on [0, 1]2. (Similarly for left- and right-continuity.)
A t-norm is called strict if it is continuous and strictly monotone
.
A t-norm is called nilpotent if it is continuous and each x in the open interval (0, 1) is its nilpotent
element, i.e., there is a natural number n such that x ...
...  x (n times) equals 0.
x (n times) equals 0.
A t-norm is called Archimedean if it has the Archimedean property
is called Archimedean if it has the Archimedean property
, i.e., if for each x, y in the open interval (0, 1) there is a natural number n such that x ...
...  x (n times) is less than or equal to y.
x (n times) is less than or equal to y.
The usual partial ordering of t-norms is pointwise, i.e.,
As functions, pointwise larger t-norms are sometimes called stronger than those pointwise smaller. In the semantics of fuzzy logic, however, the larger a t-norm, the weaker (in terms of logical strength) conjunction it represents.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a t-norm (also T-norm or, unabbreviated, triangular norm) is a kind of binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
used in the framework of probabilistic metric space
Probabilistic metric space
A probabilistic metric space is a generalization of metric spaces where the distance is no longer defined on positive real numbers, but on distribution functions....
s and in multi-valued logic
Multi-valued logic
In logic, a many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition...
, specifically in fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
. A t-norm generalizes intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
in a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
and conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
in logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
. The name triangular norm refers to the fact that in the framework of probabilistic metric spaces t-norms are used to generalize triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
of ordinary metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s.
Definition
A t-norm is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
T: [0, 1] × [0, 1] → [0, 1] which satisfies the following properties:
- CommutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
: T(a, b) = T(b, a) - Monotonicity: T(a, b) ≤ T(c, d) if a ≤ c and b ≤ d
- AssociativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
: T(a, T(b, c)) = T(T(a, b), c) - The number 1 acts as identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
: T(a, 1) = a
Since a t-norm is a binary algebraic operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
on the interval [0, 1], infix algebraic notation is also common, with the t-norm usually denoted by
 .
.The defining conditions of the t-norm are exactly those of the partially ordered Abelian monoid on the real unit interval [0, 1]. (Cf. ordered group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
.) The monoidal operation of any partially ordered Abelian monoid L is therefore by some authors called a triangular norm on L.
Motivations and applications
T-norms are a generalization of the usual two-valued logical conjunctionLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
, studied by classical logic, for fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
s. Indeed, the classical Boolean conjunction is both commutative and associative. The monotonicity property ensures that the degree of truth of conjunction does not decrease if the truth values of conjuncts increase. The requirement that 1 be an identity element corresponds to the interpretation of 1 as true (and consequently 0 as false). Continuity, which is often required from fuzzy conjunction as well, expresses the idea that, roughly speaking, very small changes in truth values of conjuncts should not macroscopically affect the truth value of their conjunction.
T-norms are also used to construct the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of fuzzy set
Fuzzy set
Fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced simultaneously by Lotfi A. Zadeh and Dieter Klaua in 1965 as an extension of the classical notion of set. In classical set theory, the membership of elements in a set is assessed in binary terms according to...
s or as a basis for aggregation operators (see fuzzy set operations
Fuzzy set operations
A fuzzy set operation is an operation on fuzzy sets. These operations are generalization of crisp set operations. There is more than one possible generalization. The most widely used operations are called standard fuzzy set operations...
). In probabilistic metric space
Probabilistic metric space
A probabilistic metric space is a generalization of metric spaces where the distance is no longer defined on positive real numbers, but on distribution functions....
s, t-norms are used to generalize triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
of ordinary metric spaces. Individual t-norms may of course frequently occur in further disciplines of mathematics, since the class contains many familiar functions.
Classification of t-norms
A t-norm is called continuous if it is continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
as a function, in the usual interval topology on [0, 1]2. (Similarly for left- and right-continuity.)
A t-norm is called strict if it is continuous and strictly monotone
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
.
A t-norm is called nilpotent if it is continuous and each x in the open interval (0, 1) is its nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
element, i.e., there is a natural number n such that x
 ...
...  x (n times) equals 0.
x (n times) equals 0.A t-norm
 is called Archimedean if it has the Archimedean property
is called Archimedean if it has the Archimedean propertyArchimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
, i.e., if for each x, y in the open interval (0, 1) there is a natural number n such that x
 ...
...  x (n times) is less than or equal to y.
x (n times) is less than or equal to y.The usual partial ordering of t-norms is pointwise, i.e.,
- T1 ≤ T2 if T1(a, b) ≤ T2(a, b) for all a, b in [0, 1].
As functions, pointwise larger t-norms are sometimes called stronger than those pointwise smaller. In the semantics of fuzzy logic, however, the larger a t-norm, the weaker (in terms of logical strength) conjunction it represents.
Prominent examples

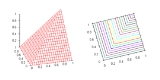
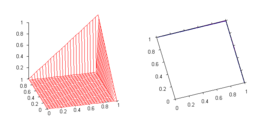
- Minimum t-norm
 also called the Gōdel t-norm, as it is the standard semantics for conjunction in Gōdel fuzzy logic. Besides that, it occurs in most t-norm based fuzzy logics as the standard semantics for weak conjunction. It is the pointwise largest t-norm (see the properties of t-norms below).
also called the Gōdel t-norm, as it is the standard semantics for conjunction in Gōdel fuzzy logic. Besides that, it occurs in most t-norm based fuzzy logics as the standard semantics for weak conjunction. It is the pointwise largest t-norm (see the properties of t-norms below).

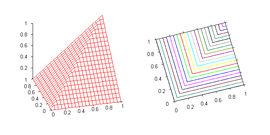
- Product t-norm
 (the ordinary product of real numbers). Besides other uses, the product t-norm is the standard semantics for strong conjunction in product fuzzy logic. It is a strict Archimedean t-norm.
(the ordinary product of real numbers). Besides other uses, the product t-norm is the standard semantics for strong conjunction in product fuzzy logic. It is a strict Archimedean t-norm.

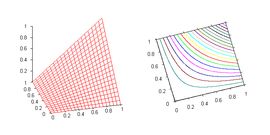
- Łukasiewicz t-norm
 The name comes from the fact that the t-norm is the standard semantics for strong conjunction in Łukasiewicz fuzzy logic. It is a nilpotent Archimedean t-norm, pointwise smaller than the product t-norm.
The name comes from the fact that the t-norm is the standard semantics for strong conjunction in Łukasiewicz fuzzy logic. It is a nilpotent Archimedean t-norm, pointwise smaller than the product t-norm.

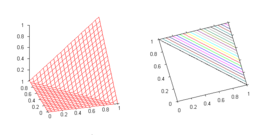
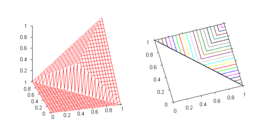
- Drastic t-norm
-

- The name reflects the fact that the drastic t-norm is the pointwise smallest t-norm (see the properties of t-norms below). It is a right-continuous Archimedean t-norm.
- Nilpotent minimum
-

- is a standard example of a t-norm which is left-continuous, but not continuous. Despite its name, the nilpotent minimum is not a nilpotent t-norm.

- Hamacher product
-

- is a strict Archimedean t-norm, and an important representative of the parametric classes of Hamacher t-norms and Schweizer–Sklar t-norms.
Properties of t-norms
The drastic t-norm is the pointwise smallest t-norm and the minimum is the pointwise largest t-norm: for any t-norm
for any t-norm  and all a, b in [0, 1].
and all a, b in [0, 1].
For every t-norm T, the number 0 acts as null element: T(a, 0) = 0 for all a in [0, 1].
A t-norm T has zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s if and only if it has nilpotent elements; each nilpotent element of T is also a zero divisor of T. The set of all nilpotent elements is an interval [0, a] or [0, a), for some a in [0, 1].
Properties of continuous t-norms
Although real functions of two variables can be continuous in each variable without being continuous on [0, 1]2, this is not the case with t-norms: a t-norm T is continuous if and only if it is continuous in one variable, i.e., if and only if the functions fy(x) = T(x, y) are continuous for each y in [0, 1]. Analogous theorems hold for left- and right-continuity of a t-norm.
A continuous t-norm is Archimedean if and only if 0 and 1 are its only idempotents.
A continuous Archimedean t-norm is strict if 0 is its only nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
element; otherwise it is nilpotent. By definition, moreover, a continuous Archimedean t-norm T is nilpotent if and only if each x < 1 is a nilpotent element of T. Thus with a continuous Archimedean t-norm T, either all or none of the elements of (0, 1) are nilpotent. If it is the case that all elements in (0, 1) are nilpotent, then the t-norm is isomorphic to the Łukasiewicz t-norm; i.e., there is a strictly increasing function f such that
If on the other hand it is the case that there are no nilpotent elements of T, the t-norm is isomorphic to the product t-norm. In other words, all nilpotent t-norms are isomorphic, the Łukasiewicz t-norm being their prototypical representative; and all strict t-norms are isomorphic, with the product t-norm as their prototypical example. The Łukasiewicz t-norm is itself isomorphic to the product t-norm undercut at 0.25, i.e., to the function p(x, y) = max(0.25, x · y) on [0.25, 1]2.
For each continuous t-norm, the set of its idempotents is a closed subset of [0, 1]. Its complement — the set of all elements which are not idempotent — is therefore a union of countably many non-overlapping open intervals. The restriction of the t-norm to any of these intervals (including its endpoints) is Archimedean, and thus isomorphic either to the Łukasiewicz t-norm or the product t-norm. For such x, y that do not fall into the same open interval of non-idempotents, the t-norm evaluates to the minimum of x and y. These conditions actually give a characterization of continuous t-norms, called the Mostert–Shields theorem, since every continuous t-norm can in this way be decomposed, and the described construction always yields a continuous t-norm. The theorem can also be formulated as follows:- A t-norm is continuous if and only if it is isomorphic to an ordinal sum of the minimum, Łukasiewicz, and product t-norm.
A similar characterization theorem for non-continuous t-norms is not known (not even for left-continuous ones), only some non-exhaustive methods for the construction of t-normsConstruction of t-normsIn mathematics, t-norms are a special kind of binary operations on the real unit interval [0, 1]. Various constructions of t-norms, either by explicit definition or by transformation from previously known functions, provide a plenitude of examples and classes of t-norms...
have been found.
Residuum
For any left-continuous t-norm , there is a unique binary operation
, there is a unique binary operation  on [0, 1] such that
on [0, 1] such that if and only if
if and only if 
for all x, y, z in [0, 1]. This operation is called the residuum of the t-norm. In prefix notation, the residuum to a t-norm is often denoted by
is often denoted by  or by the letter R.
or by the letter R.
The interval [0, 1] equipped with a t-norm and its residuum forms a residuated latticeResiduated latticeIn abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
. The relation between a t-norm T and its residuum R is an instance of adjunction: the residuum forms a right adjoint R(x, –) to the functor T(–, x) for each x in the lattice [0, 1] taken as a poset category.
In the standard semantics of t-norm based fuzzy logics, where conjunction is interpreted by a t-norm, the residuum plays the role of implication (often called R-implication).
Basic properties of residua
If is the residuum of a left-continuous t-norm
is the residuum of a left-continuous t-norm  , then
, then
Consequently, for all x, y in the unit interval, if and only if
if and only if 
and
If is a left-continuous t-norm and
is a left-continuous t-norm and  its residuum, then
its residuum, then
If is continuous, then equality holds in the former.
is continuous, then equality holds in the former.
Residua of prominent left-continuous t-norms
If x ≤ y, then R(x, y) = 1 for any residuum R. The following table therefore gives the values of prominent residua only for x > y.
Residuum of the Name Value for x > y Graph Minimum t-norm Standard Gōdel implication y 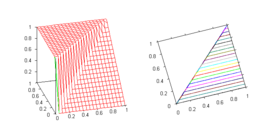
Product t-norm Goguen Joseph GoguenJoseph Amadee Goguen was a computer science professor in the Department of Computer Science and Engineering at the University of California, San Diego, USA, who helped develop the OBJ family of programming languages. He was author of A Categorical Manifesto and founder and Editor-in-Chief of the...
implicationy / x 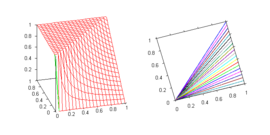
Łukasiewicz t-norm Standard Łukasiewicz implication 1 – x + y 
Nilpotent minimum max(1 – x, y) 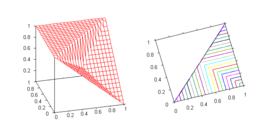
T-conorms
T-conorms (also called S-norms) are dual to t-norms under the order-reversing operation which assigns 1 – x to x on [0, 1]. Given a t-norm, the complementary conorm is defined by
This generalizes De Morgan's laws.
It follows that a t-conorm satisfies the following conditions, which can be used for an equivalent axiomatic definition of t-conorms independently of t-norms:- Commutativity: ⊥(a, b) = ⊥(b, a)
- Monotonicity: ⊥(a, b) ≤ ⊥(c, d) if a ≤ c and b ≤ d
- Associativity: ⊥(a, ⊥(b, c)) = ⊥(⊥(a, b), c)
- Identity element: ⊥(a, 0) = a
T-conorms are used to represent logical disjunctionLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
in fuzzy logicFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
and unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
in fuzzy set theory.
Examples of t-conorms
Important t-conorms are those dual to prominent t-norms:
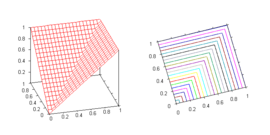
- Maximum t-conorm
 , dual to the minimum t-norm, is the smallest t-conorm (see the properties of t-conorms below). It is the standard semantics for disjunction in Gödel fuzzy logic and for weak disjunction in all t-norm based fuzzy logics.
, dual to the minimum t-norm, is the smallest t-conorm (see the properties of t-conorms below). It is the standard semantics for disjunction in Gödel fuzzy logic and for weak disjunction in all t-norm based fuzzy logics.
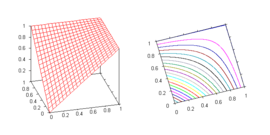
- Probabilistic sum
 is dual to the product t-norm. In probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
is dual to the product t-norm. In probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
it expresses the probability of the union of independent eventEvent (probability theory)In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
s. It is also the standard semantics for strong disjunction in such extensions of product fuzzy logic in which it is definable (e.g., those containing involutive negation).
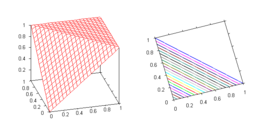
- Bounded sum
 is dual to the Łukasiewicz t-norm. It is the standard semantics for strong disjunction in Łukasiewicz fuzzy logic.
is dual to the Łukasiewicz t-norm. It is the standard semantics for strong disjunction in Łukasiewicz fuzzy logic.
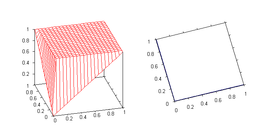
- Drastic t-conorm
-

- dual to the drastic t-norm, is the largest t-conorm (see the properties of t-conorms below).
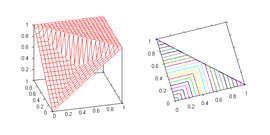
- Nilpotent maximum, dual to the nilpotent minimum:
-


- Einstein sum (compare the velocity-addition formulaVelocity-addition formulaIn physics, a velocity-addition formula is an equation that relates the velocities of moving objects in different reference frames.- Galilean addition of velocities :...
under special relativity)
-
- is a dual to one of the Hamacher t-norms.
Properties of t-conorms
Many properties of t-conorms can be obtained by dualizing the properties of t-norms, for example:- For any t-conorm ⊥, the number 1 is an annihilating element: ⊥(a, 1) = 1, for any a in [0, 1].
- Dually to t-norms, all t-conorms are bounded by the maximum and the drastic t-conorm:
-
 , for any t-conorm
, for any t-conorm  and all a, b in [0, 1].
and all a, b in [0, 1].
Further properties result from the relationships between t-norms and t-conorms or their interplay with other operators, e.g.:- A t-norm T distributesDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over a t-conorm S, i.e.,
-
- T(x, S(y, z)) = S(T(x, y), T(x, z)) for all x, y, z in [0, 1],
- if and only if S is the maximum t-conorm. Dually, any t-conorm distributes over the minimum, but not over any other t-norm.
- Einstein sum (compare the velocity-addition formula



