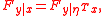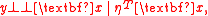Sufficient dimension reduction
Encyclopedia
In statistics
, sufficient dimension reduction (SDR) is a paradigm for analyzing data that combines the ideas of dimension reduction with the concept of sufficiency.
Dimension reduction has long been a primary goal of regression analysis
. Given a response variable y and a p-dimensional predictor vector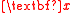 , regression analysis aims to study the distribution of
, regression analysis aims to study the distribution of 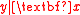 , the conditional distribution
, the conditional distribution
of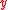 given
given 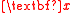 . A dimension reduction is a function
. A dimension reduction is a function  that maps
that maps 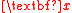 to a subset of
to a subset of  , k < p, thereby reducing the dimension
, k < p, thereby reducing the dimension
of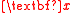 . For example,
. For example,  may be one or more linear combinations of
may be one or more linear combinations of 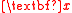 .
.
A dimension reduction is said to be sufficient if the distribution of
is said to be sufficient if the distribution of 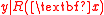 is the same as that of
is the same as that of 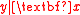 . In other words, no information about the regression is lost in reducing the dimension of
. In other words, no information about the regression is lost in reducing the dimension of 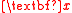 if the reduction is sufficient.
if the reduction is sufficient.
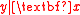 graphically. For instance, one may consider a scatter plot of
graphically. For instance, one may consider a scatter plot of 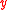 versus one or more of the predictors. A scatter plot that contains all available regression information is called a sufficient summary plot.
versus one or more of the predictors. A scatter plot that contains all available regression information is called a sufficient summary plot.
When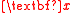 is high-dimensional, particularly when
is high-dimensional, particularly when  , it becomes increasingly challenging to construct and visually interpret sufficiency summary plots without reducing the data. Even three-dimensional scatter plots must be viewed via a computer program, and the third dimension can only be visualized by rotating the coordinate axes. However, if there exists a sufficient dimension reduction
, it becomes increasingly challenging to construct and visually interpret sufficiency summary plots without reducing the data. Even three-dimensional scatter plots must be viewed via a computer program, and the third dimension can only be visualized by rotating the coordinate axes. However, if there exists a sufficient dimension reduction  with small enough dimension, a sufficient summary plot of
with small enough dimension, a sufficient summary plot of 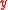 versus
versus  may be constructed and visually interpreted with relative ease.
may be constructed and visually interpreted with relative ease.
Hence sufficient dimension reduction allows for graphical intuition about the distribution of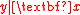 , which might not have otherwise been available for high-dimensional data.
, which might not have otherwise been available for high-dimensional data.
Most graphical methodology focuses primarily on dimension reduction involving linear combinations of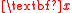 . The rest of this article deals only with such reductions.
. The rest of this article deals only with such reductions.
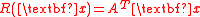 is a sufficient dimension reduction, where
is a sufficient dimension reduction, where  is a
is a 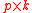 matrix
matrix
with rank
 . Then the regression information for
. Then the regression information for 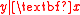 can be inferred by studying the distribution of
can be inferred by studying the distribution of  , and the plot of
, and the plot of 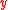 versus
versus  is a sufficient summary plot.
is a sufficient summary plot.
Without loss of generality
, only the space
spanned
by the columns of need be considered. Let
need be considered. Let 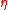 be a basis
be a basis
for the column space of , and let the space spanned by
, and let the space spanned by 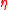 be denoted by
be denoted by 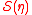 . It follows from the definition of a sufficient dimension reduction that
. It follows from the definition of a sufficient dimension reduction that
where denotes the appropriate distribution function
denotes the appropriate distribution function
. Another way to express this property is
or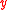 is conditionally independent
is conditionally independent
of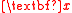 , given
, given  . Then the subspace
. Then the subspace 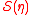 is defined to be a dimension reduction subspace (DRS).
is defined to be a dimension reduction subspace (DRS).
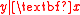 , the structural dimension,
, the structural dimension,  , is the smallest number of distinct linear combinations of
, is the smallest number of distinct linear combinations of 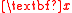 necessary to preserve the conditional distribution of
necessary to preserve the conditional distribution of 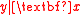 . In other words, the smallest dimension reduction that is still sufficient maps
. In other words, the smallest dimension reduction that is still sufficient maps 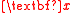 to a subset of
to a subset of 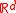 . The corresponding DRS will be d-dimensional.
. The corresponding DRS will be d-dimensional.
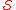 is said to be a minimum DRS for
is said to be a minimum DRS for 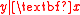 if it is a DRS and its dimension is less than or equal to that of all other DRSs for
if it is a DRS and its dimension is less than or equal to that of all other DRSs for 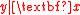 . A minimum DRS
. A minimum DRS 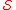 is not necessarily unique, but its dimension is equal to the structural dimension
is not necessarily unique, but its dimension is equal to the structural dimension  of
of 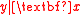 , by definition.
, by definition.
If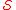 has basis
has basis 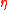 and is a minimum DRS, then a plot of y versus
and is a minimum DRS, then a plot of y versus  is a minimal sufficient summary plot, and it is (d + 1)-dimensional.
is a minimal sufficient summary plot, and it is (d + 1)-dimensional.
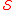 is a DRS for
is a DRS for 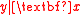 , and if
, and if 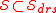 for all other DRSs
for all other DRSs 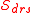 , then it is a central dimension reduction subspace, or simply a central subspace, and it is denoted by
, then it is a central dimension reduction subspace, or simply a central subspace, and it is denoted by 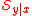 . In other words, a central subspace for
. In other words, a central subspace for 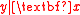 exists if and only if
exists if and only if
the intersection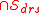 of all dimension reduction subspaces is also a dimension reduction subspace, and that intersection is the central subspace
of all dimension reduction subspaces is also a dimension reduction subspace, and that intersection is the central subspace 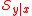 .
.
The central subspace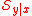 does not necessarily exist because the intersection
does not necessarily exist because the intersection 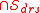 is not necessarily a DRS. However, if
is not necessarily a DRS. However, if 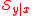 does exist, then it is also the unique minimum dimension reduction subspace.
does exist, then it is also the unique minimum dimension reduction subspace.
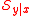 is not guaranteed in every regression situation, there are some rather broad conditions under which its existence follows directly. For example, consider the following proposition from Cook (1998):
is not guaranteed in every regression situation, there are some rather broad conditions under which its existence follows directly. For example, consider the following proposition from Cook (1998):
It follows from this proposition that the central subspace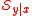 exists for such
exists for such 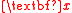 .
.
More recent methods for dimension reduction include likelihood
-based sufficient dimension reduction, estimating the central subspace based on the inverse third moment
(or kth moment), estimating the central solution space, and graphical regression. For more details on these and other methods, consult the statistical literature.
Principal components analysis
(PCA) and similar methods for dimension reduction are not based on the sufficiency principle.
Note that the distribution of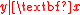 is the same as the distribution of
is the same as the distribution of  . Hence, the span of
. Hence, the span of 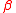 is a dimension reduction subspace. Also,
is a dimension reduction subspace. Also, 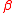 is 1-dimensional (unless
is 1-dimensional (unless 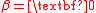 ), so the structural dimension of this regression is
), so the structural dimension of this regression is  .
.
The OLS
estimate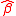 of
of 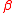 is consistent
is consistent
, and so the span of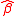 is a consistent estimator of
is a consistent estimator of 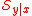 . The plot of
. The plot of 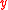 versus
versus  is a sufficient summary plot for this regression.
is a sufficient summary plot for this regression.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, sufficient dimension reduction (SDR) is a paradigm for analyzing data that combines the ideas of dimension reduction with the concept of sufficiency.
Dimension reduction has long been a primary goal of regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
. Given a response variable y and a p-dimensional predictor vector
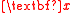 , regression analysis aims to study the distribution of
, regression analysis aims to study the distribution of 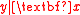 , the conditional distribution
, the conditional distributionConditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
of
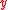 given
given 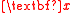 . A dimension reduction is a function
. A dimension reduction is a function  that maps
that maps 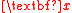 to a subset of
to a subset of 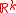 , k < p, thereby reducing the dimension
, k < p, thereby reducing the dimensionDimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of
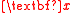 . For example,
. For example,  may be one or more linear combinations of
may be one or more linear combinations of 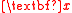 .
.A dimension reduction
 is said to be sufficient if the distribution of
is said to be sufficient if the distribution of 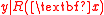 is the same as that of
is the same as that of 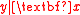 . In other words, no information about the regression is lost in reducing the dimension of
. In other words, no information about the regression is lost in reducing the dimension of 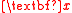 if the reduction is sufficient.
if the reduction is sufficient.Graphical motivation
In a regression setting, it is often useful to summarize the distribution of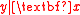 graphically. For instance, one may consider a scatter plot of
graphically. For instance, one may consider a scatter plot of 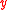 versus one or more of the predictors. A scatter plot that contains all available regression information is called a sufficient summary plot.
versus one or more of the predictors. A scatter plot that contains all available regression information is called a sufficient summary plot.When
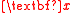 is high-dimensional, particularly when
is high-dimensional, particularly when  , it becomes increasingly challenging to construct and visually interpret sufficiency summary plots without reducing the data. Even three-dimensional scatter plots must be viewed via a computer program, and the third dimension can only be visualized by rotating the coordinate axes. However, if there exists a sufficient dimension reduction
, it becomes increasingly challenging to construct and visually interpret sufficiency summary plots without reducing the data. Even three-dimensional scatter plots must be viewed via a computer program, and the third dimension can only be visualized by rotating the coordinate axes. However, if there exists a sufficient dimension reduction  with small enough dimension, a sufficient summary plot of
with small enough dimension, a sufficient summary plot of 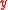 versus
versus  may be constructed and visually interpreted with relative ease.
may be constructed and visually interpreted with relative ease.Hence sufficient dimension reduction allows for graphical intuition about the distribution of
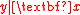 , which might not have otherwise been available for high-dimensional data.
, which might not have otherwise been available for high-dimensional data.Most graphical methodology focuses primarily on dimension reduction involving linear combinations of
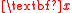 . The rest of this article deals only with such reductions.
. The rest of this article deals only with such reductions.Dimension reduction subspace
Suppose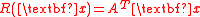 is a sufficient dimension reduction, where
is a sufficient dimension reduction, where  is a
is a 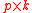 matrix
matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
 . Then the regression information for
. Then the regression information for 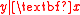 can be inferred by studying the distribution of
can be inferred by studying the distribution of  , and the plot of
, and the plot of 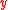 versus
versus  is a sufficient summary plot.
is a sufficient summary plot.Without loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
, only the space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
spanned
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
by the columns of
 need be considered. Let
need be considered. Let 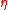 be a basis
be a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the column space of
 , and let the space spanned by
, and let the space spanned by 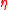 be denoted by
be denoted by 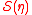 . It follows from the definition of a sufficient dimension reduction that
. It follows from the definition of a sufficient dimension reduction thatwhere
 denotes the appropriate distribution function
denotes the appropriate distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
. Another way to express this property is
or
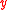 is conditionally independent
is conditionally independentConditional independence
In probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
of
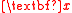 , given
, given  . Then the subspace
. Then the subspace 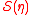 is defined to be a dimension reduction subspace (DRS).
is defined to be a dimension reduction subspace (DRS).Structural dimensionality
For a regression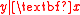 , the structural dimension,
, the structural dimension,  , is the smallest number of distinct linear combinations of
, is the smallest number of distinct linear combinations of 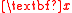 necessary to preserve the conditional distribution of
necessary to preserve the conditional distribution of 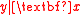 . In other words, the smallest dimension reduction that is still sufficient maps
. In other words, the smallest dimension reduction that is still sufficient maps 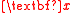 to a subset of
to a subset of  . The corresponding DRS will be d-dimensional.
. The corresponding DRS will be d-dimensional.Minimum dimension reduction subspace
A subspace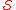 is said to be a minimum DRS for
is said to be a minimum DRS for 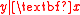 if it is a DRS and its dimension is less than or equal to that of all other DRSs for
if it is a DRS and its dimension is less than or equal to that of all other DRSs for 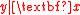 . A minimum DRS
. A minimum DRS 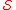 is not necessarily unique, but its dimension is equal to the structural dimension
is not necessarily unique, but its dimension is equal to the structural dimension  of
of 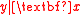 , by definition.
, by definition.If
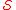 has basis
has basis 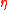 and is a minimum DRS, then a plot of y versus
and is a minimum DRS, then a plot of y versus  is a minimal sufficient summary plot, and it is (d + 1)-dimensional.
is a minimal sufficient summary plot, and it is (d + 1)-dimensional.Central subspace
If a subspace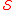 is a DRS for
is a DRS for 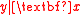 , and if
, and if 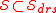 for all other DRSs
for all other DRSs 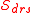 , then it is a central dimension reduction subspace, or simply a central subspace, and it is denoted by
, then it is a central dimension reduction subspace, or simply a central subspace, and it is denoted by 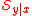 . In other words, a central subspace for
. In other words, a central subspace for 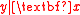 exists if and only if
exists if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the intersection
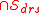 of all dimension reduction subspaces is also a dimension reduction subspace, and that intersection is the central subspace
of all dimension reduction subspaces is also a dimension reduction subspace, and that intersection is the central subspace 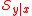 .
.The central subspace
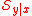 does not necessarily exist because the intersection
does not necessarily exist because the intersection 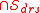 is not necessarily a DRS. However, if
is not necessarily a DRS. However, if 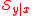 does exist, then it is also the unique minimum dimension reduction subspace.
does exist, then it is also the unique minimum dimension reduction subspace.Existence of the central subspace
While the existence of the central subspace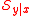 is not guaranteed in every regression situation, there are some rather broad conditions under which its existence follows directly. For example, consider the following proposition from Cook (1998):
is not guaranteed in every regression situation, there are some rather broad conditions under which its existence follows directly. For example, consider the following proposition from Cook (1998):- Let
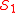 and
and 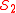 be dimension reduction subspaces for
be dimension reduction subspaces for 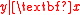 . If
. If 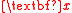 has densityProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
has densityProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
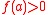 for all
for all 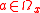 and
and 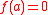 everywhere else, where
everywhere else, where 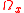 is convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
is convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, then the intersection is also a dimension reduction subspace.
is also a dimension reduction subspace.
It follows from this proposition that the central subspace
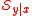 exists for such
exists for such 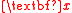 .
.Methods for dimension reduction
There are many existing methods for dimension reduction, both graphical and numeric. For example, sliced inverse regression (SIR) and sliced average variance estimation (SAVE) were introduced in the 1990s and continue to be widely-used. Although SIR was originally designed to estimate an effective dimension reducing subspace, it is now understood that it estimates only the central subspace, which is generally different.More recent methods for dimension reduction include likelihood
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
-based sufficient dimension reduction, estimating the central subspace based on the inverse third moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
(or kth moment), estimating the central solution space, and graphical regression. For more details on these and other methods, consult the statistical literature.
Principal components analysis
Principal components analysis
Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
(PCA) and similar methods for dimension reduction are not based on the sufficiency principle.
Example: linear regression
Consider the regression modelNote that the distribution of
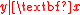 is the same as the distribution of
is the same as the distribution of  . Hence, the span of
. Hence, the span of 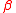 is a dimension reduction subspace. Also,
is a dimension reduction subspace. Also, 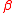 is 1-dimensional (unless
is 1-dimensional (unless 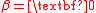 ), so the structural dimension of this regression is
), so the structural dimension of this regression is  .
.The OLS
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
estimate
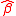 of
of 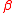 is consistent
is consistentConsistent estimator
In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
, and so the span of
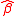 is a consistent estimator of
is a consistent estimator of 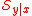 . The plot of
. The plot of 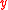 versus
versus  is a sufficient summary plot for this regression.
is a sufficient summary plot for this regression.See also
- Dimension reduction
- Sliced inverse regression
- Principal component analysis
- Linear discriminant analysisLinear discriminant analysisLinear discriminant analysis and the related Fisher's linear discriminant are methods used in statistics, pattern recognition and machine learning to find a linear combination of features which characterizes or separates two or more classes of objects or events...
- Curse of dimensionalityCurse of dimensionalityThe curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...