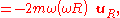
Rotating spheres
Encyclopedia
Isaac Newton
's rotating spheres argument attempts to demonstrate that true rotational motion
can be defined by observing the tension in the string joining two identical spheres. The basis of the argument is that all observers make two observations: the tension in the string joining the bodies (which is the same for all observers) and the rate of rotation of the spheres (which is different for observers with differing rates of rotation). Only for the truly stationary observer will the tension in the string be explained using only the observed rate of rotation. For all other observers a "correction" is required (a centrifugal force) that accounts for the tension calculated being different than the one expected using the observed rate of rotation. It is one of five argument
s from the "properties, causes, and effects" of true motion and rest that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space. Alternatively, these experiments provide an operational definition
of what is meant by "absolute rotation", and do not pretend to address the question of "rotation relative to what?".
). As an example where causes can be observed, if two globe
s, floating in space
, are connected by a cord, measuring the amount of tension
in the cord, with no other clues to assess the situation, alone suffices to indicate how fast the two objects are revolving around the common center of mass. (This experiment involves observation of a force, the tension). Also, the sense of the rotation —whether it is in the clockwise or the counter-clockwise direction— can be discovered by applying forces to opposite faces of the globes and ascertaining whether this leads to an increase or a decrease in the tension of the cord (again involving a force). Alternatively, the sense of the rotation can be determined by measuring the apparent motion of the globes with respect to a background system of bodies that, according to the preceding methods, have been established already as not in a state of rotation, as an example from Newton's time, the fixed stars.
In the 1846 Andrew Motte translation of Newton's words:
To summarize this proposal, here is a quote from Born:
Mach took some issue with the argument, pointing out that the rotating sphere experiment could never be done in an empty universe, where possibly Newton's laws do not apply, so the experiment really only shows what happens when the spheres rotate in our universe, and therefore, for example, may indicate only rotation relative to the entire mass of the universe.
An interpretation that avoids this conflict is to say that the rotating spheres experiment does not really define rotation relative to anything in particular (for example, absolute space or fixed stars); rather the experiment is an operational definition
of what is meant by the motion called absolute rotation.
amusement ride, you do not need much convincing that you are rotating, but standing on the Earth's surface, the matter is more subtle.) Below, the mathematical details behind this observation are presented.
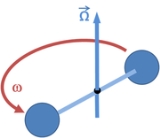
Figure 1 shows two identical spheres rotating about the center of the string joining them. The axis of rotation is shown as a vector Ω with direction given by the right-hand rule
and magnitude equal to the rate of rotation: |Ω| = ω. The angular rate of rotation ω is assumed independent of time (uniform circular motion
). Because of the rotation, the string is under tension. (See reactive centrifugal force
.) The description of this system next is presented from the viewpoint of an inertial frame and from a rotating frame of reference.
. The other ball has the same requirement, but being on the opposite end of the string, requires a centripetal force of the same size, but opposite in direction. See Figure 2. These two forces are provided by the string, putting the string under tension, also shown in Figure 2.
:

where uR is a unit vector pointing from the axis of rotation to one of the spheres, and Ω is a vector representing the angular rotation, with magnitude ω and direction normal to the plane of rotation
given by the right-hand rule
, m is the mass of the ball, and R is the distance from the axis of rotation to the spheres (the magnitude of the displacement vector, |xB| = R, locating one or the other of the spheres). According to the rotating observer, shouldn't the tension in the string be twice as big as before (the tension from the centrifugal force plus the extra tension needed to provide the centripetal force of rotation)? The reason the rotating observer sees zero tension is because of yet another fictitious force in the rotating world, the Coriolis force, which depends on the velocity of a moving object. In this zero-tension case, according to the rotating observer the spheres now are moving, and the Coriolis force (which depends upon velocity) is activated. According to the article fictitious force
, the Coriolis force is:
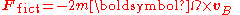
where R is the distance to the object from the center of rotation, and vB is the velocity of the object subject to the Coriolis force, |vB| = ωR.
In the geometry of this example, this Coriolis force has twice the magnitude of the ubiquitous centrifugal force and is exactly opposite in direction. Therefore, it cancels out the ubiquitous centrifugal force found in the first example, and goes a step further to provide exactly the centripetal force demanded by uniform circular motion, so the rotating observer calculates there is no need for tension in the string − the Coriolis force looks after everything.

This force also is the force due to tension seen by the rotating observers. The rotating observers see the spheres in circular motion with angular rate ωS = ωI − ωR (S = spheres). That is, if the frame rotates more slowly than the spheres, ωS > 0 and the spheres advance counterclockwise around a circle, while for a more rapidly moving frame, ωS < 0, and the spheres appear to retreat clockwise around a circle. In either case, the rotating observers see circular motion and require a net inward centripetal force:
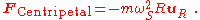
However, this force is not the tension in the string. So the rotational observers conclude that a force exists (which the inertial observers call a fictitious force) so that:
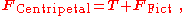
or,
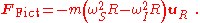
The fictitious force changes sign depending upon which of ωI and ωS is greater. The reason for the sign change is that when ωI > ωS, the spheres actually are moving faster than the rotating observers measure, so they measure a tension in the string that actually is larger than they expect; hence, the fictitious force must increase the tension (point outward). When ωI < ωS, things are reversed so the fictitious force has to decrease the tension, and therefore has the opposite sign (points inward).
The introduction of FFict allows the rotational observers and the inertial observers to agree on the tension in the string. However, we might ask: "Does this solution fit in with general experience with other situations, or is it simply a "cooked up" ad hoc
solution?" That question is answered by seeing how this value for FFict squares with the general result (derived in Fictitious force
):
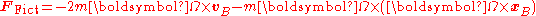
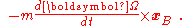
The subscript B refers to quantities referred to the non-inertial coordinate system. Full notational details are in Fictitious force. For constant angular rate of rotation the last term is zero. To evaluate the other terms we need the position of one of the spheres:

and the velocity of this sphere as seen in the rotating frame:
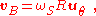
where uθ is a unit vector perpendicular to uR pointing in the direction of motion.
The frame rotates at a rate ωR, so the vector of rotation is Ω = ωR uz (uz a unit vector in the z-direction), and Ω × uR = ωR (uz × uR) = ωR uθ ; Ω × uθ = −ωR uR. The centrifugal force is then: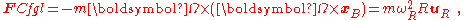
which naturally depends only on the rate of rotation of the frame and is always outward. The Coriolis force is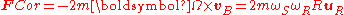
and has the ability to change sign, being outward when the spheres move faster than the frame ( ωS > 0 ) and being inward when the spheres move slower than the frame ( ωS < 0 ). Combining the terms:

Consequently, the fictitious force found above for this problem of rotating spheres is consistent with the general result and is not an ad hoc
solution just "cooked up" to bring about agreement for this single example. Moreover, it is the Coriolis force that makes it possible for the fictitious force to change sign depending upon which of ωI, ωS is the greater, inasmuch as the centrifugal force contribution always is outward.
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's rotating spheres argument attempts to demonstrate that true rotational motion
Rotation around a fixed axis
Rotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...
can be defined by observing the tension in the string joining two identical spheres. The basis of the argument is that all observers make two observations: the tension in the string joining the bodies (which is the same for all observers) and the rate of rotation of the spheres (which is different for observers with differing rates of rotation). Only for the truly stationary observer will the tension in the string be explained using only the observed rate of rotation. For all other observers a "correction" is required (a centrifugal force) that accounts for the tension calculated being different than the one expected using the observed rate of rotation. It is one of five argument
Argument
In philosophy and logic, an argument is an attempt to persuade someone of something, or give evidence or reasons for accepting a particular conclusion.Argument may also refer to:-Mathematics and computer science:...
s from the "properties, causes, and effects" of true motion and rest that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space. Alternatively, these experiments provide an operational definition
Operational definition
An operational definition defines something in terms of the specific process or set of validation tests used to determine its presence and quantity. That is, one defines something in terms of the operations that count as measuring it. The term was coined by Percy Williams Bridgman and is a part of...
of what is meant by "absolute rotation", and do not pretend to address the question of "rotation relative to what?".
Background
Newton was concerned to address the problem of how it is that we can experimentally determine the true motions of bodies in light of the fact that absolute space is not something that can be perceived. Such determination, he says, can be accomplished by observing the causes of motion (that is, forces) and not simply the apparent motions of bodies relative to one another (as in the bucket argumentBucket argument
Isaac Newton's rotating bucket argument was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies...
). As an example where causes can be observed, if two globe
Globe
A globe is a three-dimensional scale model of Earth or other spheroid celestial body such as a planet, star, or moon...
s, floating in space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
, are connected by a cord, measuring the amount of tension
Tension (mechanics)
In physics, tension is the magnitude of the pulling force exerted by a string, cable, chain, or similar object on another object. It is the opposite of compression. As tension is the magnitude of a force, it is measured in newtons and is always measured parallel to the string on which it applies...
in the cord, with no other clues to assess the situation, alone suffices to indicate how fast the two objects are revolving around the common center of mass. (This experiment involves observation of a force, the tension). Also, the sense of the rotation —whether it is in the clockwise or the counter-clockwise direction— can be discovered by applying forces to opposite faces of the globes and ascertaining whether this leads to an increase or a decrease in the tension of the cord (again involving a force). Alternatively, the sense of the rotation can be determined by measuring the apparent motion of the globes with respect to a background system of bodies that, according to the preceding methods, have been established already as not in a state of rotation, as an example from Newton's time, the fixed stars.
In the 1846 Andrew Motte translation of Newton's words:
To summarize this proposal, here is a quote from Born:
Mach took some issue with the argument, pointing out that the rotating sphere experiment could never be done in an empty universe, where possibly Newton's laws do not apply, so the experiment really only shows what happens when the spheres rotate in our universe, and therefore, for example, may indicate only rotation relative to the entire mass of the universe.
An interpretation that avoids this conflict is to say that the rotating spheres experiment does not really define rotation relative to anything in particular (for example, absolute space or fixed stars); rather the experiment is an operational definition
Operational definition
An operational definition defines something in terms of the specific process or set of validation tests used to determine its presence and quantity. That is, one defines something in terms of the operations that count as measuring it. The term was coined by Percy Williams Bridgman and is a part of...
of what is meant by the motion called absolute rotation.


Formulation of the argument
This sphere example was used by Newton himself to discuss the detection of rotation relative to absolute space. Checking the fictitious force needed to account for the tension in the string is one way for an observer to decide whether or not they are rotating – if the fictitious force is zero, they are not rotating. (Of course, in an extreme case like the gravitronGravitron
The Gravitron is an amusement ride, most commonly found as a portable ride at fairs and carnivals. The Gravitron first appeared at Morey's Piers in 1983 and quickly became a fixture at amusement parks in many countries. It is a modification of an earlier ride called the Rotor...
amusement ride, you do not need much convincing that you are rotating, but standing on the Earth's surface, the matter is more subtle.) Below, the mathematical details behind this observation are presented.
Figure 1 shows two identical spheres rotating about the center of the string joining them. The axis of rotation is shown as a vector Ω with direction given by the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
and magnitude equal to the rate of rotation: |Ω| = ω. The angular rate of rotation ω is assumed independent of time (uniform circular motion
Uniform circular motion
In physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends...
). Because of the rotation, the string is under tension. (See reactive centrifugal force
Reactive centrifugal force
In classical mechanics, reactive centrifugal force is the reaction paired with centripetal force. A mass undergoing circular motion constantly accelerates toward the axis of rotation. This centripetal acceleration is caused by a force exerted on the mass by some other object. In accordance with...
.) The description of this system next is presented from the viewpoint of an inertial frame and from a rotating frame of reference.
Inertial frame
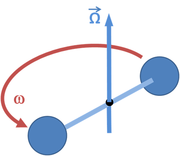
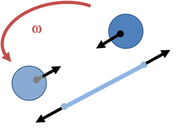
Adopt an inertial frame centered at the midpoint of the string. The balls move in a circle about the origin of our coordinate system. Look first at one of the two balls. To travel in a circular path, which is not uniform motion with constant velocity, but circular motion at constant speed, requires a force to act on the ball so as to continuously change the direction of its velocity. This force is directed inward, along the direction of the string, and is called a centripetal forceCentripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
. The other ball has the same requirement, but being on the opposite end of the string, requires a centripetal force of the same size, but opposite in direction. See Figure 2. These two forces are provided by the string, putting the string under tension, also shown in Figure 2.
Rotating frame
Adopt a rotating frame at the midpoint of the string. Suppose the frame rotates at the same angular rate as the balls, so the balls appear stationary in this rotating frame. Because the balls are not moving, observers say they are at rest. If they now apply Newton's law of inertia, they would say no force acts on the balls, so the string should be relaxed. However, they clearly see the string is under tension. (For example, they could split the string and put a spring in its center, which would stretch.) To account for this tension, they propose that in their frame a centrifugal force acts on the two balls, pulling them apart. This force originates from nowhere – it is just a "fact of life" in this rotating world, and acts on everything they observe, not just these spheres. In resisting this ubiquitous centrifugal force, the string is placed under tension, accounting for their observation, despite the fact that the spheres are at rest.Coriolis force
What if the spheres are not rotating in the inertial frame (string tension is zero)? Then string tension in the rotating frame also is zero. But how can that be? The spheres in the rotating frame now appear to be rotating, and should require an inward force to do that. According to the analysis of uniform circular motionUniform circular motion
In physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends...
:

where uR is a unit vector pointing from the axis of rotation to one of the spheres, and Ω is a vector representing the angular rotation, with magnitude ω and direction normal to the plane of rotation
Plane of rotation
In geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
given by the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
, m is the mass of the ball, and R is the distance from the axis of rotation to the spheres (the magnitude of the displacement vector, |xB| = R, locating one or the other of the spheres). According to the rotating observer, shouldn't the tension in the string be twice as big as before (the tension from the centrifugal force plus the extra tension needed to provide the centripetal force of rotation)? The reason the rotating observer sees zero tension is because of yet another fictitious force in the rotating world, the Coriolis force, which depends on the velocity of a moving object. In this zero-tension case, according to the rotating observer the spheres now are moving, and the Coriolis force (which depends upon velocity) is activated. According to the article fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
, the Coriolis force is:
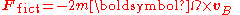
where R is the distance to the object from the center of rotation, and vB is the velocity of the object subject to the Coriolis force, |vB| = ωR.
In the geometry of this example, this Coriolis force has twice the magnitude of the ubiquitous centrifugal force and is exactly opposite in direction. Therefore, it cancels out the ubiquitous centrifugal force found in the first example, and goes a step further to provide exactly the centripetal force demanded by uniform circular motion, so the rotating observer calculates there is no need for tension in the string − the Coriolis force looks after everything.
General case
What happens if the spheres rotate at one angular rate, say ωI (I = inertial), and the frame rotates at a different rate ωR (R = rotational)? The inertial observers see circular motion and the tension in the string exerts a centripetal inward force on the spheres of:
This force also is the force due to tension seen by the rotating observers. The rotating observers see the spheres in circular motion with angular rate ωS = ωI − ωR (S = spheres). That is, if the frame rotates more slowly than the spheres, ωS > 0 and the spheres advance counterclockwise around a circle, while for a more rapidly moving frame, ωS < 0, and the spheres appear to retreat clockwise around a circle. In either case, the rotating observers see circular motion and require a net inward centripetal force:
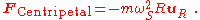
However, this force is not the tension in the string. So the rotational observers conclude that a force exists (which the inertial observers call a fictitious force) so that:
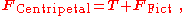
or,
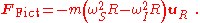
The fictitious force changes sign depending upon which of ωI and ωS is greater. The reason for the sign change is that when ωI > ωS, the spheres actually are moving faster than the rotating observers measure, so they measure a tension in the string that actually is larger than they expect; hence, the fictitious force must increase the tension (point outward). When ωI < ωS, things are reversed so the fictitious force has to decrease the tension, and therefore has the opposite sign (points inward).
Is the fictitious force ad hoc?
The introduction of FFict allows the rotational observers and the inertial observers to agree on the tension in the string. However, we might ask: "Does this solution fit in with general experience with other situations, or is it simply a "cooked up" ad hoc
Ad hoc
Ad hoc is a Latin phrase meaning "for this". It generally signifies a solution designed for a specific problem or task, non-generalizable, and not intended to be able to be adapted to other purposes. Compare A priori....
solution?" That question is answered by seeing how this value for FFict squares with the general result (derived in Fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
):
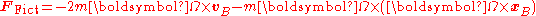
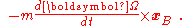
The subscript B refers to quantities referred to the non-inertial coordinate system. Full notational details are in Fictitious force. For constant angular rate of rotation the last term is zero. To evaluate the other terms we need the position of one of the spheres:

and the velocity of this sphere as seen in the rotating frame:
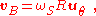
where uθ is a unit vector perpendicular to uR pointing in the direction of motion.
The frame rotates at a rate ωR, so the vector of rotation is Ω = ωR uz (uz a unit vector in the z-direction), and Ω × uR = ωR (uz × uR) = ωR uθ ; Ω × uθ = −ωR uR. The centrifugal force is then:
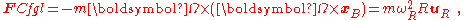
which naturally depends only on the rate of rotation of the frame and is always outward. The Coriolis force is
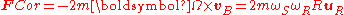
and has the ability to change sign, being outward when the spheres move faster than the frame ( ωS > 0 ) and being inward when the spheres move slower than the frame ( ωS < 0 ). Combining the terms:


Consequently, the fictitious force found above for this problem of rotating spheres is consistent with the general result and is not an ad hoc
Ad hoc
Ad hoc is a Latin phrase meaning "for this". It generally signifies a solution designed for a specific problem or task, non-generalizable, and not intended to be able to be adapted to other purposes. Compare A priori....
solution just "cooked up" to bring about agreement for this single example. Moreover, it is the Coriolis force that makes it possible for the fictitious force to change sign depending upon which of ωI, ωS is the greater, inasmuch as the centrifugal force contribution always is outward.
Rotation and cosmic background radiation
The isotropy of the cosmic background radiation is another indicator that the universe does not rotate.See also
- Bucket argumentBucket argumentIsaac Newton's rotating bucket argument was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies...
- Centrifugal force (rotating reference frame)
- Fictitious forceFictitious forceA fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
- Mach's principleMach's principleIn theoretical physics, particularly in discussions of gravitation theories, Mach's principle is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach....
- Mechanics of planar particle motionMechanics of planar particle motionThis article describes a particle in planar motion when observed from non-inertial reference frames. The most famous examples of planar motion are related to the motion of two spheres that are gravitationally attracted to one another, and the generalization of this problem to planetary motion....
- Sagnac effectSagnac effectThe Sagnac effect , named after French physicist Georges Sagnac, is a phenomenon encountered in interferometry that is elicited by rotation. The Sagnac effect manifests itself in a setup called ring interferometry. A beam of light is split and the two beams are made to follow a trajectory in...
- Wilkinson Microwave Anisotropy ProbeWilkinson Microwave Anisotropy ProbeThe Wilkinson Microwave Anisotropy Probe — also known as the Microwave Anisotropy Probe , and Explorer 80 — is a spacecraft which measures differences in the temperature of the Big Bang's remnant radiant heat — the Cosmic Microwave Background Radiation — across the full sky. Headed by Professor...