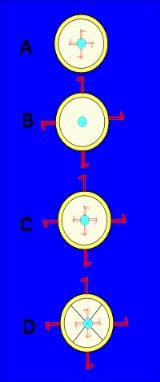
Bucket argument
Overview
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's rotating bucket argument (also known as "Newton's bucket") was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies. It is one of five argument
Argument
In philosophy and logic, an argument is an attempt to persuade someone of something, or give evidence or reasons for accepting a particular conclusion.Argument may also refer to:-Mathematics and computer science:...
s from the "properties, causes, and effects" of true motion and rest that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space.
Discussions

