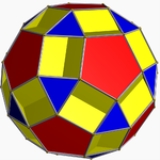
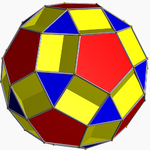
Rhombicosidodecahedron
Encyclopedia
In geometry
, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid
, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon
face
s.
It has 20 regular triangular faces, 30 square
faces, 12 regular pentagon
al faces, 60 vertices and 120 edges.
The name rhombicosidodecahedron refers to the fact that the 30 square faces lie in the same planes as the 30 faces of the rhombic triacontahedron
which is dual to the icosidodecahedron
.
It can also be called an expanded
or cantellated
dodecahedron or icosahedron, from truncation operations on either uniform polyhedron
.
an icosahedron
by moving the faces away from the origin
the right amount, without changing the orientation or size of the faces, and do the same to its dual
dodecahedron, and patch the square holes in the result, you get a rhombicosidodecahedron. Therefore, it has the same number of triangles as an icosahedron and the same number of pentagons as a dodecahedron, with a square for each edge of either.
The rhombicosidodecahedron shares the vertex arrangement with the small stellated truncated dodecahedron, and with the uniform compounds of 6 or 12 pentagrammic prism
s.
The Zometool kits for making geodesic dome
s and other polyhedra use slotted balls as connectors. The balls are "expanded" small rhombicosidodecahedra, with the squares replaced by rectangles. The expansion is chosen so that the resulting rectangles are golden rectangles.
Twelve of the 92 Johnson solid
s are derived from the rhombicosidodecahedron, four of them by rotation of one or more pentagonal cupola
s: the gyrate
, parabigyrate
, metabigyrate
and trigyrate rhombicosidodecahedron
. Eight more can be constructed by removing up to three cupolas, sometimes also rotating one or more of the other cupolas.
where φ = (1+√5)/2 is the golden ratio
(also written τ).
 The rhombicosidodecahedron shares its vertex arrangement
The rhombicosidodecahedron shares its vertex arrangement
with 3 nonconvex uniform polyhedra
: the small stellated truncated dodecahedron, the small dodecicosidodecahedron
(having the triangular and pentagonal faces in common), and the small rhombidodecahedron
(having the square faces in common).
It also shares its vertex arrangement with the uniform compounds of 6
or 12 pentagrammic prisms
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
s.
It has 20 regular triangular faces, 30 square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
faces, 12 regular pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
al faces, 60 vertices and 120 edges.
The name rhombicosidodecahedron refers to the fact that the 30 square faces lie in the same planes as the 30 faces of the rhombic triacontahedron
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
which is dual to the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
.
It can also be called an expanded
Expansion (geometry)
In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements...
or cantellated
Cantellation (geometry)
In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
dodecahedron or icosahedron, from truncation operations on either uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
.
Geometric relations
If you blow upExpansion (geometry)
In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements...
an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
by moving the faces away from the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
the right amount, without changing the orientation or size of the faces, and do the same to its dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
dodecahedron, and patch the square holes in the result, you get a rhombicosidodecahedron. Therefore, it has the same number of triangles as an icosahedron and the same number of pentagons as a dodecahedron, with a square for each edge of either.
The rhombicosidodecahedron shares the vertex arrangement with the small stellated truncated dodecahedron, and with the uniform compounds of 6 or 12 pentagrammic prism
Pentagrammic prism
In geometry, the pentagrammic prism is one in an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U78 as a uniform polyhedron....
s.
The Zometool kits for making geodesic dome
Geodesic dome
A geodesic dome is a spherical or partial-spherical shell structure or lattice shell based on a network of great circles on the surface of a sphere. The geodesics intersect to form triangular elements that have local triangular rigidity and also distribute the stress across the structure. When...
s and other polyhedra use slotted balls as connectors. The balls are "expanded" small rhombicosidodecahedra, with the squares replaced by rectangles. The expansion is chosen so that the resulting rectangles are golden rectangles.
Twelve of the 92 Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s are derived from the rhombicosidodecahedron, four of them by rotation of one or more pentagonal cupola
Pentagonal cupola
In geometry, the pentagonal cupola is one of the Johnson solids . It can be obtained as a slice of the rhombicosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966....
s: the gyrate
Gyrate rhombicosidodecahedron
In geometry, the gyrate rhombicosidodecahedron is one of theJohnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.- Related polyhedron :...
, parabigyrate
Parabigyrate rhombicosidodecahedron
In geometry, the parabigyrate rhombicosidodecahedron is one of the Johnson solids . It can be constructed as a rhombicosidodecahedron with two opposing pentagonal cupolae rotated through 36 degrees....
, metabigyrate
Metabigyrate rhombicosidodecahedron
In geometry, the metabigyrate rhombicosidodecahedron is one of the Johnson solids . It can be constructed as a rhombicosidodecahedron with two non-opposing pentagonal cupolae rotated through 36 degrees....
and trigyrate rhombicosidodecahedron
Trigyrate rhombicosidodecahedron
In geometry, the trigyrate rhombicosidodecahedron is one of theJohnson solids .It can be constructed as a rhombicosidodecahedron with three pentagonal cupolae rotated through 36 degrees.Related Johnson solids are...
. Eight more can be constructed by removing up to three cupolas, sometimes also rotating one or more of the other cupolas.
Cartesian coordinates
Cartesian coordinates for the vertices of a rhombicosidodecahedron with edge length 2 centered at the origin are:- (±1, ±1, ±φ3),
- (±φ3, ±1, ±1),
- (±1, ±φ3, ±1),
- (±φ2, ±φ, ±2φ),
- (±2φ, ±φ2, ±φ),
- (±φ, ±2φ, ±φ2),
- (±(2+φ), 0, ±φ2),
- (±φ2, ±(2+φ), 0),
- (0, ±φ2, ±(2+φ)),
where φ = (1+√5)/2 is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
(also written τ).
Orthogonal projections
The rhombicosidodecahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: triangles and pentagons. The last two correspond to the A2 and H2 Coxeter planes.| Centered by | Vertex | Edge 3-4 |
Edge 5-4 |
Face Triangle |
Face Pentagon |
|---|---|---|---|---|---|
| Image | |||||
| Projective symmetry |
[2] | [2] | [2] | [6] | [10] |
Related polyhedra

Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
with 3 nonconvex uniform polyhedra
Nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
: the small stellated truncated dodecahedron, the small dodecicosidodecahedron
Small dodecicosidodecahedron
In geometry, the small dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U33. Its vertex figure is a crossed quadrilateral.-Related polyhedra:...
(having the triangular and pentagonal faces in common), and the small rhombidodecahedron
Small rhombidodecahedron
In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...
(having the square faces in common).
It also shares its vertex arrangement with the uniform compounds of 6
Compound of six pentagrammic prisms
This uniform polyhedron compound is a chiral symmetric arrangement of 6 pentagrammic prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.- Related polyhedra :...
or 12 pentagrammic prisms
Compound of twelve pentagrammic prisms
This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.It results from composing the two enantiomorphs of the compound of six pentagrammic prisms...
.
 Rhombicosidodecahedron |
 Small dodecicosidodecahedron Small dodecicosidodecahedron In geometry, the small dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U33. Its vertex figure is a crossed quadrilateral.-Related polyhedra:... |
 Small rhombidodecahedron Small rhombidodecahedron In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... |
 Small stellated truncated dodecahedron |
 Compound of six pentagrammic prisms Compound of six pentagrammic prisms This uniform polyhedron compound is a chiral symmetric arrangement of 6 pentagrammic prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.- Related polyhedra :... |
 Compound of twelve pentagrammic prisms Compound of twelve pentagrammic prisms This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.It results from composing the two enantiomorphs of the compound of six pentagrammic prisms... |
See also
- Spinning rhombicosidodecahedron
- dodecahedron
- icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
- icosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
- rhombicuboctahedronRhombicuboctahedronIn geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
- truncated icosidodecahedronTruncated icosidodecahedronIn geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
(great rhombicosidodecahedron)
External links
- http://www.dr-mikes-math-games-for-kids.com/polyhedral-nets.html?net=Tv7E5gwABUaM2ZveUSXfe07idxu9JkCNMCUPlvFp6IcoHTplD9zjAVEMTaqWv564CpAoS7XNSNgGaNIj1rKA9ZH27MMImTFBlDuu244zzn7T8pKfEoWr9dWHdB7M4mLvUgqz0qTPdTXv3lmuoNVKKoLzM7J4pgVXDeHRT5aRUXQLS77vVHlxGdPrT13N8Ad7LAjAAT68r7qz1fG5TMbsOhgpTLxNvbyyUqQyhP5BNkpGLDUZ9ifqSECYogSuKygW3HeESpNO1XGeziqxukeTQndGewnUQL1gl2DhAscHn3rN5LcdzzrjBOtMjqjAkfMnJ1U5zok8P8BJAp5OktxCBC7fC0IVLU6NGOphHnm0AcJz2VZuGkrFFtc213K59mwMsBQpO0cOVxiAi23LEuz0EwylrWVWusgcxkRZMvqwFXXLCLCSavdB1vIH7NfTWEAo5nJvuqigk9Cwy1R5vUOBMNOsjCrKPQsZaxQ5xayCFJX1NaDJzqWMyKEf4JxDEjWTmI0Y4YYq6Q8t7T0V4THzBezQ3z55EZZK0LSe5cwtZag&name=Rhombicosidodecahedron#appletEditable printable net of a Rhombicosidodecahedron with interactive 3D view]
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- The Rhombi-Cosi-Dodecahedron Website
- The Rhombicosidodecahedron as a 3D puzzle

