Resampling (statistics)
Encyclopedia
In statistics
, resampling is any of a variety of methods for doing one of the following:
Common resampling techniques include bootstrapping, jackknifing and permutation tests.
of an estimator
by sampling
with replacement from the original sample, most often with the purpose of deriving robust estimates of standard error
s and confidence intervals of a population parameter like a mean
, median
, proportion
, odds ratio
, correlation coefficient
or regression
coefficient. It may also be used for constructing hypothesis tests. It is often used as a robust alternative to inference based on parametric assumptions when those assumptions are in doubt, or where parametric inference is impossible or requires very complicated formulas for the calculation of standard errors.
to estimate the bias and standard error (variance) of a statistic, when a random sample of observations is used to calculate it. The basic idea behind the jackknife variance estimator lies in systematically recomputing the statistic estimate leaving out one or more observations at a time from the sample set. From this new set of replicates of the statistic, an estimate for the bias and an estimate for the variance of the statistic can be calculated.
Both methods, the bootstrap and the jackknife, estimate the variability of a statistic from the variability of that statistic between subsamples, rather than from parametric assumptions. The jackknife can be seen as more or less general than the bootstrap depending on the way both are perceived. For the more general jackknife, the delete-m observations jackknife, the bootstrap can be seen as a random approximation of it. Both yield similar numerical results, which is why each can be seen as approximation to the other. Although there are huge theoretical differences in their mathematical insights, the main practical difference for statistics users is that the bootstrap
gives different results when repeated on the same data, whereas the jackknife gives exactly the same result each time. Because of this, the jackknife is popular when the estimates need to be verified several times before publishing (e.g. official statistics agencies). On the other hand, when this verification feature is not crucial and it is of interest not to have a number but just an idea of its distribution the bootstrap is preferred (e.g. studies in physics, economics, biological sciences).
Whether to use bootstrap or jackknife may depend more on non-statistical concerns but on operational aspects of a survey. The bootstrap provides a powerful and easy way to estimate not just the variance of a point estimator but its whole distribution, thus becoming highly computer intensive. On the other hand, the jackknife (originally used for bias reduction) only provides estimates of the variance of the point estimator. This can be enough for basic statistical inference (e.g. hypothesis testing, confidence intervals). Hence, the jackknife is a specialized method for estimating variances whereas the bootstrap first estimates the whole distribution from where the variance is assessed.
"The bootstrap can be applied to both variance and distribution estimation problems. However, the bootstrap variance estimator is not as good as the jackknife or the BRR variance estimator in terms of the empirical results. Furthermore, the bootstrap variance estimator usually requires more computations than the jackknife or the BRR. Thus, the bootstrap is mainly recommended for distribution estimation."
There is a special consideration with the jackknife, particularly with the delete-1 observation jackknife. It should only be used with smooth differentiable statistics, that is: totals, means, proportions, ratios, odd ratios, regression coefficients, etc.; but not with medians or quantiles. This clearly may become a practical disadvantage or not depending on the needs of the user. This disadvantage is usually the argument against the jackknife in benefit to the bootstrap. More general jackknifes than the delete-1, such as the delete-m jackknife, overcome this problem for the medians and quantiles by relaxing the smoothness requirements for consistent variance estimation.
Usually the jackknife is easier to apply to complex sampling schemes than the bootstrap. Complex sampling schemes may involve stratification, multi-stages (clustering), varying sampling weights (non-response adjustments, calibration, post-stratification) and under unequal-probability sampling designs. Theoretical aspects of both the bootstrap and the jackknife can be found in, whereas a basic introduction is accounted in.
One form of cross-validation leaves out a single observation at a time; this is similar to the jackknife. Another, K-fold cross-validation, splits the data into K subsets; each is held out in turn as the validation set.
This avoids "self-influence". For comparison, in regression analysis
methods such as linear regression
, each y value draws the regression line toward itself, making the prediction of that value appear more accurate than it really is. Cross-validation applied to linear regression predicts the y value for each observation without using that observation.
This is often used for deciding how many predictor variables to use in regression. Without cross-validation, adding predictors always reduces the residual sum of squares (or possibly leaves it unchanged). In contrast, the cross-validated mean-square error will tend to decrease if valuable predictors are added, but increase if worthless predictors are added.
) is a type of statistical significance test
in which the distribution of the test statistic under the null hypothesis is obtained by calculating all possible values of the test statistic
under rearrangements of the labels on the observed data points. In other words, the method by which treatments are allocated to subjects in an experimental design is mirrored in the analysis of that design. If the labels are exchangeable under the null hypothesis, then the resulting tests yield exact significance levels; see also exchangeability. Confidence intervals can then be derived from the tests. The theory has evolved from the works of R.A. Fisher and E.J.G. Pitman in the 1930s.
To illustrate the basic idea of a permutation test,
suppose we have two groups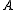
and 
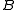whose sample means
are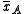
and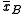
,
and that we want to test, at 5% significance level, whether they come from the same distribution.
Let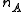
and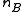 
be the sample
size corresponding to each group.
The permutation test is designed to
determine whether the observed difference
between the sample means is large enough
to reject the null hypothesis H
that
the two groups have identical probability distribution.
The test proceeds as follows.
First, the difference in means between the two samples is calculated: this is the observed value of the test statistic, T(obs). Then the observations of groups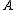
and 
are pooled.
Next, the difference in sample means is calculated and recorded for every possible way of dividing these pooled values into two groups of size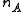
and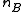 
(i.e., for every permutation of the group labels A and B). The set of these calculated differences is the exact distribution of possible differences under the null hypothesis that group label does not matter.
The one-sided p-value of the test is calculated as the proportion of sampled permutations where the difference in means was greater than or equal to T(obs).
The two-sided p-value of the test is calculated as the proportion of sampled permutations where the absolute difference
was greater than or equal to ABS(T(obs)).
If the only purpose of the test is reject or not reject the null hypothesis, we can as an alternative sort the recorded differences, and then observe if T(obs) is contained within the middle 95% of them. If it is not, we reject the hypothesis of identical probability curves at the 5% significant level.
. The basic premise is to use only the assumption that it is possible that all of the treatment groups are equivalent, and that every member of them is the same before sampling began (i.e. the slot that they fill is not differentiable from other slots before the slots are filled). From this, one can calculate a statistic and then see to what extent this statistic is special by seeing how likely it would be if the treatment assignments had been jumbled.
In contrast to permutation tests, the reference distributions for many popular "classical" statistical tests, such as the t-test, F-test
, z-test
and χ2 test, are obtained from theoretical probability distributions.
Fisher's exact test
is an example of a commonly used permutation test for evaluating the association between two dichotomous variables. When sample sizes are large, the Pearson's chi-square test will give accurate results. For small samples, the chi-square reference distribution cannot be assumed to give a correct description of the probability distribution of the test statistic, and in this situation the use of Fisher's exact test becomes more appropriate. A rule of thumb is that the expected count in each cell of the table should be greater than 5 before Pearson's chi-squared test is used.
Permutation tests exist in many situations where parametric tests do not (e.g., when deriving an optimal test when losses are proportional to the size of an error rather than its square). All simple and many relatively complex parametric tests have a corresponding permutation test version that is defined by using the same test statistic as the parametric test, but obtains the p-value from the sample-specific permutation distribution of that statistic, rather than from the theoretical distribution derived from the parametric assumption. For example, it is possible in this manner to construct a permutation t-test, a permutation chi-squared test of association, a permutation version of Aly's test for comparing variances and so on.
The major down-side to permutation tests are that they
.
Permutation tests can be used for analyzing unbalanced designs and for combining dependent tests on mixtures of categorical, ordinal, and metric data (Pesarin, 2001).
Before the 1980s, the burden of creating the reference distribution was overwhelming except for data sets with small sample sizes.
Since the 1980s, the confluence of relatively inexpensive fast computers and the development of new sophisticated path algorithms applicable in special situations, made the application of permutation test methods practical for a wide range of problems. It also initiated the addition of exact-test options in the main statistical software packages and the appearance of specialized software for performing a wide range of uni- and multi-variable exact tests and computing test-based "exact" confidence intervals.
The realization that this could be applied to any permutation test on any dataset was an important breakthrough in the area of applied statistics. The earliest known reference to this approach is Dwass (1957).
This type of permutation test is known under various names: approximate permutation test, Monte Carlo permutation tests or random permutation tests.
The necessary size of the Monte Carlo sample depends on the need for accuracy of the test. If one merely wants to know if the p-value is significant, sometimes as few as 400 rearrangements is sufficient to generate a reliable answer. However, for most scientific applications the required size is much higher. For observed p=0.05, the accuracy from 10,000 random permutations is 0.0056 and for 50,000 it is 0.0025. For observed p=0.01, the corresponding accuracy is 0.0077 and 0.0035. Accuracy is defined from the binomial 99% confidence interval: p +/- accuracy.
Modern references:
Computational methods:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, resampling is any of a variety of methods for doing one of the following:
- Estimating the precision of sample statisticStatisticA statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
s (medianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
s, varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s, percentilePercentileIn statistics, a percentile is the value of a variable below which a certain percent of observations fall. For example, the 20th percentile is the value below which 20 percent of the observations may be found...
s) by using subsets of available data (jackknifing) or drawing randomly with replacement from a set of data points (bootstrappingBootstrapping (statistics)In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
) - Exchanging labels on data points when performing significance tests (permutation tests, also called exact testExact testIn statistics, an exact test is a test where all assumptions upon which the derivation of the distribution of the test statistic is based are met, as opposed to an approximate test, in which the approximation may be made as close as desired by making the sample size big enough...
s, randomization tests, or re-randomization tests) - Validating models by using random subsets (bootstrapping, cross validation)
Common resampling techniques include bootstrapping, jackknifing and permutation tests.
Bootstrap
Bootstrapping is a statistical method for estimating the sampling distributionSampling distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference...
of an estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
by sampling
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
with replacement from the original sample, most often with the purpose of deriving robust estimates of standard error
Standard error
Standard error can refer to:* Standard error , the estimated standard deviation or error of a series of measurements* Standard error stream, one of the standard streams in Unix-like operating systems...
s and confidence intervals of a population parameter like a mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
, proportion
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
, odds ratio
Odds ratio
The odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic, and plays an important role in logistic regression...
, correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
or regression
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
coefficient. It may also be used for constructing hypothesis tests. It is often used as a robust alternative to inference based on parametric assumptions when those assumptions are in doubt, or where parametric inference is impossible or requires very complicated formulas for the calculation of standard errors.
Jackknife
Jackknifing, which is similar to bootstrapping, is used in statistical inferenceStatistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
to estimate the bias and standard error (variance) of a statistic, when a random sample of observations is used to calculate it. The basic idea behind the jackknife variance estimator lies in systematically recomputing the statistic estimate leaving out one or more observations at a time from the sample set. From this new set of replicates of the statistic, an estimate for the bias and an estimate for the variance of the statistic can be calculated.
Both methods, the bootstrap and the jackknife, estimate the variability of a statistic from the variability of that statistic between subsamples, rather than from parametric assumptions. The jackknife can be seen as more or less general than the bootstrap depending on the way both are perceived. For the more general jackknife, the delete-m observations jackknife, the bootstrap can be seen as a random approximation of it. Both yield similar numerical results, which is why each can be seen as approximation to the other. Although there are huge theoretical differences in their mathematical insights, the main practical difference for statistics users is that the bootstrap
Bootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
gives different results when repeated on the same data, whereas the jackknife gives exactly the same result each time. Because of this, the jackknife is popular when the estimates need to be verified several times before publishing (e.g. official statistics agencies). On the other hand, when this verification feature is not crucial and it is of interest not to have a number but just an idea of its distribution the bootstrap is preferred (e.g. studies in physics, economics, biological sciences).
Whether to use bootstrap or jackknife may depend more on non-statistical concerns but on operational aspects of a survey. The bootstrap provides a powerful and easy way to estimate not just the variance of a point estimator but its whole distribution, thus becoming highly computer intensive. On the other hand, the jackknife (originally used for bias reduction) only provides estimates of the variance of the point estimator. This can be enough for basic statistical inference (e.g. hypothesis testing, confidence intervals). Hence, the jackknife is a specialized method for estimating variances whereas the bootstrap first estimates the whole distribution from where the variance is assessed.
"The bootstrap can be applied to both variance and distribution estimation problems. However, the bootstrap variance estimator is not as good as the jackknife or the BRR variance estimator in terms of the empirical results. Furthermore, the bootstrap variance estimator usually requires more computations than the jackknife or the BRR. Thus, the bootstrap is mainly recommended for distribution estimation."
There is a special consideration with the jackknife, particularly with the delete-1 observation jackknife. It should only be used with smooth differentiable statistics, that is: totals, means, proportions, ratios, odd ratios, regression coefficients, etc.; but not with medians or quantiles. This clearly may become a practical disadvantage or not depending on the needs of the user. This disadvantage is usually the argument against the jackknife in benefit to the bootstrap. More general jackknifes than the delete-1, such as the delete-m jackknife, overcome this problem for the medians and quantiles by relaxing the smoothness requirements for consistent variance estimation.
Usually the jackknife is easier to apply to complex sampling schemes than the bootstrap. Complex sampling schemes may involve stratification, multi-stages (clustering), varying sampling weights (non-response adjustments, calibration, post-stratification) and under unequal-probability sampling designs. Theoretical aspects of both the bootstrap and the jackknife can be found in, whereas a basic introduction is accounted in.
Cross-validation
Cross-validation is a statistical method for validating a predictive model. Subsets of the data are held out for use as validating sets; a model is fit to the remaining data (a training set) and used to predict for the validation set. Averaging the quality of the predictions across the validation sets yields an overall measure of prediction accuracy.One form of cross-validation leaves out a single observation at a time; this is similar to the jackknife. Another, K-fold cross-validation, splits the data into K subsets; each is held out in turn as the validation set.
This avoids "self-influence". For comparison, in regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
methods such as linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
, each y value draws the regression line toward itself, making the prediction of that value appear more accurate than it really is. Cross-validation applied to linear regression predicts the y value for each observation without using that observation.
This is often used for deciding how many predictor variables to use in regression. Without cross-validation, adding predictors always reduces the residual sum of squares (or possibly leaves it unchanged). In contrast, the cross-validated mean-square error will tend to decrease if valuable predictors are added, but increase if worthless predictors are added.
Permutation tests
A permutation test (also called a randomization test, re-randomization test, or an exact testExact test
In statistics, an exact test is a test where all assumptions upon which the derivation of the distribution of the test statistic is based are met, as opposed to an approximate test, in which the approximation may be made as close as desired by making the sample size big enough...
) is a type of statistical significance test
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
in which the distribution of the test statistic under the null hypothesis is obtained by calculating all possible values of the test statistic
Test statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
under rearrangements of the labels on the observed data points. In other words, the method by which treatments are allocated to subjects in an experimental design is mirrored in the analysis of that design. If the labels are exchangeable under the null hypothesis, then the resulting tests yield exact significance levels; see also exchangeability. Confidence intervals can then be derived from the tests. The theory has evolved from the works of R.A. Fisher and E.J.G. Pitman in the 1930s.
To illustrate the basic idea of a permutation test,
suppose we have two groups
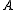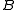and whose sample meansare
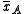
and
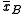,and that we want to test, at 5% significance level, whether they come from the same distribution.
Let
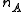and 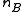be the samplesize corresponding to each group.
The permutation test is designed to
determine whether the observed difference
between the sample means is large enough
to reject the null hypothesis H
thatthe two groups have identical probability distribution.
The test proceeds as follows.
First, the difference in means between the two samples is calculated: this is the observed value of the test statistic, T(obs). Then the observations of groups
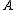and are pooled.Next, the difference in sample means is calculated and recorded for every possible way of dividing these pooled values into two groups of size
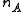and 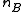(i.e., for every permutation of the group labels A and B). The set of these calculated differences is the exact distribution of possible differences under the null hypothesis that group label does not matter.The one-sided p-value of the test is calculated as the proportion of sampled permutations where the difference in means was greater than or equal to T(obs).
The two-sided p-value of the test is calculated as the proportion of sampled permutations where the absolute difference
Absolute difference
The absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...
was greater than or equal to ABS(T(obs)).
If the only purpose of the test is reject or not reject the null hypothesis, we can as an alternative sort the recorded differences, and then observe if T(obs) is contained within the middle 95% of them. If it is not, we reject the hypothesis of identical probability curves at the 5% significant level.
Relation to parametric tests
Permutation tests are a subset of non-parametric statisticsNon-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
. The basic premise is to use only the assumption that it is possible that all of the treatment groups are equivalent, and that every member of them is the same before sampling began (i.e. the slot that they fill is not differentiable from other slots before the slots are filled). From this, one can calculate a statistic and then see to what extent this statistic is special by seeing how likely it would be if the treatment assignments had been jumbled.
In contrast to permutation tests, the reference distributions for many popular "classical" statistical tests, such as the t-test, F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
, z-test
Z-test
A Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Due to the central limit theorem, many test statistics are approximately normally distributed for large samples...
and χ2 test, are obtained from theoretical probability distributions.
Fisher's exact test
Fisher's exact test
Fisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
is an example of a commonly used permutation test for evaluating the association between two dichotomous variables. When sample sizes are large, the Pearson's chi-square test will give accurate results. For small samples, the chi-square reference distribution cannot be assumed to give a correct description of the probability distribution of the test statistic, and in this situation the use of Fisher's exact test becomes more appropriate. A rule of thumb is that the expected count in each cell of the table should be greater than 5 before Pearson's chi-squared test is used.
Permutation tests exist in many situations where parametric tests do not (e.g., when deriving an optimal test when losses are proportional to the size of an error rather than its square). All simple and many relatively complex parametric tests have a corresponding permutation test version that is defined by using the same test statistic as the parametric test, but obtains the p-value from the sample-specific permutation distribution of that statistic, rather than from the theoretical distribution derived from the parametric assumption. For example, it is possible in this manner to construct a permutation t-test, a permutation chi-squared test of association, a permutation version of Aly's test for comparing variances and so on.
The major down-side to permutation tests are that they
- Can be computationally intensive and may require "custom" code for difficult-to-calculate statistics. This must be rewritten for every case.
- Are primarily used to provide a p-value. The inversion of the test to get confidence regions/intervals requires even more computation.
Examples
Permutation tests have been used to reduce the bias of categorical variable importance scores measured by information gain in decision treesInformation gain in decision trees
In information theory and machine learning, information gain is an alternative synonym for Kullback–Leibler divergence.In particular, the information gain about a random variable X obtained from an observation that a random variable A takes the value A=a is the Kullback-Leibler divergence DKL of...
.
Advantages
Permutation tests exist for any test statistic, regardless of whether or not its distribution is known. Thus one is always free to choose the statistic which best discriminates between hypothesis and alternative and which minimizes losses.Permutation tests can be used for analyzing unbalanced designs and for combining dependent tests on mixtures of categorical, ordinal, and metric data (Pesarin, 2001).
Before the 1980s, the burden of creating the reference distribution was overwhelming except for data sets with small sample sizes.
Since the 1980s, the confluence of relatively inexpensive fast computers and the development of new sophisticated path algorithms applicable in special situations, made the application of permutation test methods practical for a wide range of problems. It also initiated the addition of exact-test options in the main statistical software packages and the appearance of specialized software for performing a wide range of uni- and multi-variable exact tests and computing test-based "exact" confidence intervals.
Limitations
An important assumption behind a permutation test is that the observations are exchangeable under the null hypothesis. An important consequence of this assumption is that tests of difference in location (like a permutation t-test) require equal variance. In this respect, the permutation t-test shares the same weakness as the classical Student's t-test (the Behrens–Fisher problem). A third alternative in this situation is to use a bootstrap-based test. Good (2000) explains the difference between permutation tests and bootstrap tests the following way: "Permutations test hypotheses concerning distributions; bootstraps test hypotheses concerning parameters. As a result, the bootstrap entails less-stringent assumptions." Of course, bootstrap tests are not exact.Monte Carlo testing
An asymptotically equivalent permutation test can be created when there are too many possible orderings of the data to allow complete enumeration in a convenient manner. This is done by generating the reference distribution by Monte Carlo sampling, which takes a small (relative to the total number of permutations) random sample of the possible replicates.The realization that this could be applied to any permutation test on any dataset was an important breakthrough in the area of applied statistics. The earliest known reference to this approach is Dwass (1957).
This type of permutation test is known under various names: approximate permutation test, Monte Carlo permutation tests or random permutation tests.
The necessary size of the Monte Carlo sample depends on the need for accuracy of the test. If one merely wants to know if the p-value is significant, sometimes as few as 400 rearrangements is sufficient to generate a reliable answer. However, for most scientific applications the required size is much higher. For observed p=0.05, the accuracy from 10,000 random permutations is 0.0056 and for 50,000 it is 0.0025. For observed p=0.01, the corresponding accuracy is 0.0077 and 0.0035. Accuracy is defined from the binomial 99% confidence interval: p +/- accuracy.
See also
- Bootstrap aggregating (Bagging)Bootstrap aggregatingBootstrap aggregating is a machine learning ensemble meta-algorithm to improve machine learning of statistical classification and regression models in terms of stability and classification accuracy. It also reduces variance and helps to avoid overfitting. Although it is usually applied to decision...
- Particle filterParticle filterIn statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
- Random permutationRandom permutationA random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation...
- Monte Carlo methods
- Nonparametric statistics
Introductory statistics
- Good, P. (2005) Introduction to Statistics Through Resampling Methods and R/S-PLUS. Wiley. ISBN 0-471-71575-1
- Good, P. (2005) Introduction to Statistics Through Resampling Methods and Microsoft Office Excel. Wiley. ISBN 0-471-73191-9
- Hesterberg, T. C., D. S. Moore, S. Monaghan, A. Clipson, and R. Epstein (2005). Bootstrap Methods and Permutation Tests.
- Wolter, K.M. (2007). Introduction to Variance Estimation. Second Edition. Springer, Inc.
Bootstrapping
- Bradley EfronBradley EfronBradley Efron is an American statistician best known for proposing the bootstrap resampling technique, which has had a major impact in the field of statistics and virtually every area of statistical application...
(1979). "Bootstrap methods: Another look at the jackknife", The Annals of Statistics, 7, 1-26. - Bradley EfronBradley EfronBradley Efron is an American statistician best known for proposing the bootstrap resampling technique, which has had a major impact in the field of statistics and virtually every area of statistical application...
(1981). "Nonparametric estimates of standard error: The jackknife, the bootstrap and other methods", BiometrikaBiometrika- External links :* . The Internet Archive. 2011....
, 68, 589-599. - Bradley EfronBradley EfronBradley Efron is an American statistician best known for proposing the bootstrap resampling technique, which has had a major impact in the field of statistics and virtually every area of statistical application...
(1982). The jackknife, the bootstrap, and other resampling plans, In Society of Industrial and Applied Mathematics CBMS-NSF Monographs, 38. - P. Diaconis, Bradley EfronBradley EfronBradley Efron is an American statistician best known for proposing the bootstrap resampling technique, which has had a major impact in the field of statistics and virtually every area of statistical application...
(1983), "Computer-intensive methods in statistics," Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, May, 116-130. - Bradley EfronBradley EfronBradley Efron is an American statistician best known for proposing the bootstrap resampling technique, which has had a major impact in the field of statistics and virtually every area of statistical application...
, Robert J. Tibshirani, (1993). An introduction to the bootstrap, New York: Chapman & Hall, software. - Davison, A. C. and Hinkley, D. V. (1997): Bootstrap Methods and their Application, software.
- Mooney, C Z & Duval, R D (1993). Bootstrapping. A Nonparametric Approach to Statistical Inference. Sage University Paper series on Quantitative Applications in the Social Sciences, 07-095. Newbury Park, CA: SageSAGE PublicationsSAGE is an independent academic publisher of books, journals, and electronic products in the humanities and social sciences and the scientific, technical, and medical fields. SAGE was founded in 1965 by George McCune and Sara Miller McCune. The company is headquartered in Thousand Oaks, California,...
. - Simon, J. L. (1997): Resampling: The New Statistics.
Jackknife
- Berger, Y.G. (2007). A jackknife variance estimator for unistage stratified samples with unequal probabilities. BiometrikaBiometrika- External links :* . The Internet Archive. 2011....
. Vol. 94, 4, pp. 953–964. - Berger, Y.G. and Rao, J.N.K. (2006). Adjusted jackknife for imputation under unequal probability sampling without replacement. Journal of the Royal Statistical SocietyJournal of the Royal Statistical SocietyThe Journal of the Royal Statistical Society is a series of three peer-reviewed statistics journals published by Blackwell Publishing for the London-based Royal Statistical Society.- History :...
B. Vol. 68, 3, pp. 531–547. - Berger, Y.G. and Skinner, C.J. (2005). A jackknife variance estimator for unequal probability sampling. Journal of the Royal Statistical SocietyJournal of the Royal Statistical SocietyThe Journal of the Royal Statistical Society is a series of three peer-reviewed statistics journals published by Blackwell Publishing for the London-based Royal Statistical Society.- History :...
B. Vol. 67, 1, pp. 79–89. - Jiang, J., Lahiri, P. and Wan, S-M. (2002). A unified jackknife theory for empirical best prediction with M-estimation. The Annals of Statistics. Vol. 30, 6, pp. 1782–810.
- Jones, H.L. (1974). Jackknife estimation of functions of stratum means. BiometrikaBiometrika- External links :* . The Internet Archive. 2011....
. Vol. 61, 2, pp. 343–348. - Kish, L. and Frankel M.R. (1974). Inference from complex samples. Journal of the Royal Statistical SocietyJournal of the Royal Statistical SocietyThe Journal of the Royal Statistical Society is a series of three peer-reviewed statistics journals published by Blackwell Publishing for the London-based Royal Statistical Society.- History :...
B. Vol. 36, 1, pp. 1–37. - Krewski, D. and Rao, J.N.K. (1981). Inference from stratified samples: properties of the linearization, jackknife and balanced repeated replication methods. The Annals of Statistics. Vol. 9, 5, pp. 1010–1019.
- Quenouille, M.H. (1956). Notes on bias in estimation. BiometrikaBiometrika- External links :* . The Internet Archive. 2011....
. Vol. 43, pp. 353–360. - Rao, J.N.K. and Shao, J. (1992). Jackknife variance estimation with survey data under hot deck imputation. BiometrikaBiometrika- External links :* . The Internet Archive. 2011....
. Vol. 79, 4, pp. 811–822. - Rao, J.N.K., Wu, C.F.J. and Yue, K. (1992). Some recent work on resampling methods for complex surveys. Survey MethodologySurvey MethodologySurvey Methodology is a peer-reviewed open access scientific journal that publishes papers related to the development and application of survey techniques...
. Vol. 18, 2, pp. 209–217. - Shao, J. and Tu, D. (1995). The Jackknife and Bootstrap. Springer-Verlag, Inc.
- Tukey, J.W. (1958). Bias and confidence in not-quite large samples (abstract). The Annals of Mathematical Statistics. Vol. 29, 2, pp. 614.
- Wu, C.F.J.C.F. Jeff WuC.F. Jeff Wu is a statistician known for his work on the convergence of the EM algorithm,resampling methods like bootstrap and jackknife, design of experiments, and robust parameter design .- Notes and references :*- Sources and links :*...
(1986). Jackknife, Bootstrap and other resampling methods in regression analysis. The Annals of Statistics. Vol. 14, 4, pp. 1261–1295.
Monte Carlo methods
- George S. Fishman (1995). Monte Carlo: Concepts, Algorithms, and Applications, Springer, New York. ISBN 0-387-94527-X.
- James E. Gentle (2009). Computational Statistics, Springer, New York. Part III: Methods of Computational Statistics. ISBN 978-0-387-98143-7.
- Dirk P. Kroese, Thomas Taimre and Zdravko I. Botev. Handbook of Monte Carlo Methods, John Wiley & Sons, New York. ISBN 978-0-470-17793-8.
- Christian P. Robert and George Casella (2004). Monte Carlo Statistical Methods, Second ed., Springer, New York. ISBN 0-387-21239-6.
- Shlomo SawilowskyShlomo SawilowskyShlomo S. Sawilowsky is professor of educational statistics and Distinguished Faculty Fellow at Wayne State University in Detroit, Michigan, where he has received teaching, mentoring, and research awards.- Academic career :...
and Gail Fahoome (2003). Statistics via Monte Carlo Simulation with Fortran. Rochester Hills, MI: JMASM. ISBN 0-9740236-0-4.
Permutation test
Original references:- R. A. Fisher, The Design of Experiment, New York: HafnerHafnerHafner is a surname, and may refer to:* Dorinda Hafner* Frank Hafner* Genevieve Hafner* Ingrid Hafner* Katie Hafner* Nuala Hafner* Philipp Hafner* Raoul Hafner, , Austrian-born British helicopter pioneer and engineer....
, 1935. - Pitman, E. J. G., "Significance tests which may be applied to samples from any population", Royal Statistical Society Supplement, 1937; 4: 119-130 and 225-32 (parts I and II).
- Pitman, E. J. G., "Significance tests which may be applied to samples from any population. Part III. The analysis of variance test", BiometrikaBiometrika- External links :* . The Internet Archive. 2011....
, 1938; 29: 322-335.
Modern references:
- E. S. Edgington, Randomization tests, 3rd ed. New York: Marcel-Dekker, 1995.
- Phillip I. Good, Permutation, Parametric and Bootstrap Tests of Hypotheses, 3rd ed., SpringerSpringer Science+Business Media- Selected publications :* Encyclopaedia of Mathematics* Ergebnisse der Mathematik und ihrer Grenzgebiete * Graduate Texts in Mathematics * Grothendieck's Séminaire de géométrie algébrique...
, 2005. ISBN 0-387-98898-X - Good, P. (2002) Extensions of the concept of exchangeability and their applications, J. Modern Appl. Statist. Methods, 1:243-247.
- Lunneborg, Cliff. Data Analysis by Resampling, Duxbury Press, 1999. ISBN 0-534-22110-6.
- Pesarin, F. 2001. Multivariate Permutation Tests, John Wiley & SonsJohn Wiley & SonsJohn Wiley & Sons, Inc., also referred to as Wiley, is a global publishing company that specializes in academic publishing and markets its products to professionals and consumers, students and instructors in higher education, and researchers and practitioners in scientific, technical, medical, and...
. - Welch, W. J., Construction of permutation tests, Journal of American Statistical Association, 85:693-698, 1990.
Computational methods:
- Mehta, C. R. and Patel, N. R. (1983). 2A network algorithm for performing Fisher's exact test in r x c contingency tables", J. Amer. Statist. Assoc, 78(382):427–434.
- Metha, C. R., Patel, N. R. and Senchaudhuri, P. (1988). "Importance sampling for estimating exact probabilities in permutational inference", J. Am. Statist. Assoc., 83(404):999–1005.
Resampling methods
- Good, P. (2006) Resampling Methods. 3rd Ed. Birkhauser.
- Wolter, K.M. (2007). Introduction to Variance Estimation. 2nd Edition. Springer, Inc.
Current research on permutation tests
- Bootstrap Sampling tutorial
- Hesterberg, T. C., D. S. Moore, S. Monaghan, A. Clipson, and R. Epstein (2005): Bootstrap Methods and Permutation Tests, software.
- Moore, D. S., G. McCabe, W. Duckworth, and S. Sclove (2003): Bootstrap Methods and Permutation Tests
- Simon, J. L. (1997): Resampling: The New Statistics.
- Yu, Chong Ho (2003): Resampling methods: concepts, applications, and justification. Practical Assessment, Research & Evaluation, 8(19). (statistical bootstrapping)
- Resampling: A Marriage of Computers and Statistics (ERIC Digests)
Software
- Angelo Canty and Brian Ripley (2010). boot: Bootstrap R (S-Plus) Functions. R package version 1.2-43. Functions and datasets for bootstrapping from the book Bootstrap Methods and Their Applications by A. C. Davison and D. V. Hinkley (1997, CUP).
- Statistics101: Resampling, Bootstrap, Monte Carlo Simulation program