Schlegel diagram with the 5 tetrahedral cells shown.
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t1{3,3,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Cells	10	5 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...   5 3.3.3.3 Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
Faces	30 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
Edges	30
Vertices	10
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	Triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	A4, [3,3,3], order 120
Petrie Polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets...	Pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... , isogonal, isotoxal
Uniform index	1 Pentachoron In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the pentachoron, pentatope, or hyperpyramid... 2 3 Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...

In four dimensional geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the rectified

Rectification (geometry)

In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...

 5-cell is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

 composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

 is a triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

.

It is one of three semiregular polychora made of two or more cells which are platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

s, discovered by Thorold Gosset

Thorold Gosset

Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...

 in his 1900 paper. He called it a Tetroctahedric for being made of tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

 and octahedron

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

 cells.

The vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

 of the rectified 5-cell is a uniform triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

, formed by three octahedra

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

 around the sides, and two tetrahedra

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

 on the opposite ends.

Alternate names

• Dispentachoron
• Rectified 5-cell (Norman W. Johnson)
• Rectified 4-simplex
  Simplex
  In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
  
  
• Rectified pentachoron (Acronym: rap) (Jonathan Bowers)
• Ambopentachoron (Neil Sloane & John Horton Conway
  John Horton Conway
  John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
  
  )

Images

stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... (centered on octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... )

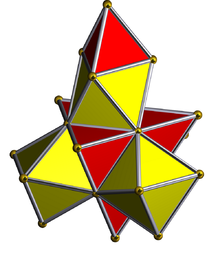Net (polytope)

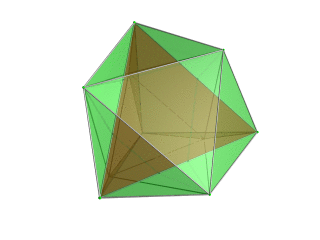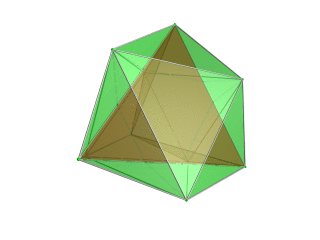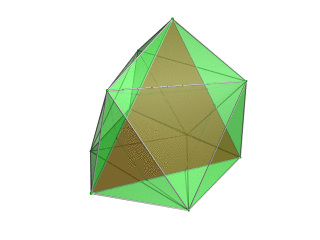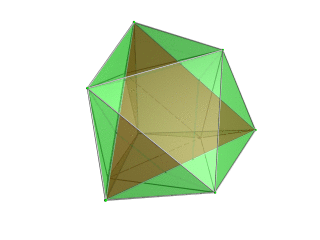Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... -centered perspective projection into 3D space, with nearest tetrahedron to the 4D viewpoint rendered in red, and the 4 surrounding octahedra in green. Cells lying on the far side of the polytope have been culled for clarity (although they can be discerned from the edge outlines). The rotation is only of the 3D projection image, in order to show its structure, not a rotation in 4D space.

Coordinates

The Cartesian coordinates of the vertices of an origin-centered rectified 5-cell having edge length 2 are: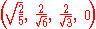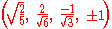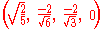


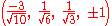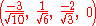More simply, the vertices of the rectified 5-cell can be positioned on a hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

 in 5-space as permutations of (0,0,0,1,1) or (0,0,1,1,1). These construction can be seen as positive orthant

Orthant

In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....

 facets of the rectified pentacross

Rectified pentacross

In five-dimensional geometry, a rectified 5-orthoplex is a convex uniform 5-polytope, being a rectification of the regular 5-orthoplex.There are 5 degrees of rectifications for any 5-polytope, the zeroth here being the 5-orthoplex itself, and the 4th and last being the 5-cube. Vertices of the...

 or birectified penteract respectively.

Related polychora

This polytope is the vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

 of the 5-demicube, and the edge figure of the uniform 2₂₁ polytope.

It is also one of 9 uniform polychora

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

 constructed from the [3,3,3] Coxeter group

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

.

External links

• Rectified 5-cell - data and images