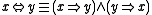Monoidal t-norm logic
Encyclopedia
Monoidal t-norm based logic (or shortly MTL), the logic of left-continuous t-norm
s, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logic
s, or logics of residuated lattice
s; it extends the logic of commutative bounded integral residuated lattices (known as Höhle's monoidal logic, Ono's FLew, or intuitionistic logic without contraction) by the axiom of prelinearity.
s are binary functions on the real unit interval [0, 1] which are often used to represent a conjunction connective in fuzzy logic
. Every left-continuous t-norm has a unique residuum, that is, a function
has a unique residuum, that is, a function 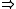 such that for all x, y, and z,
such that for all x, y, and z,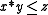 if and only if
if and only if 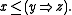
The residuum of a left-continuous t-norm can explicitly be defined as
This ensures that the residuum is the largest function such that for all x and y,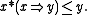
The latter can be interpreted as a fuzzy version of the modus ponens
rule of inference. The residuum of a left-continuous t-norm thus can be characterized as the weakest function that makes the fuzzy modus ponens valid, which makes it a suitable truth function for implication in fuzzy logic. Left-continuity of the t-norm is the necessary and sufficient condition for this relationship between a t-norm conjunction and its residual implication to hold.
Truth functions of further propositional connectives can be defined by means of the t-norm and its residuum, for instance the residual negation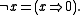 In this way, the left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives (see the section Standard semantics below) determine the truth values of complex propositional formula
In this way, the left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives (see the section Standard semantics below) determine the truth values of complex propositional formula
e in [0, 1]. Formulae that always evaluate to 1 are then called tautologies
with respect to the given left-continuous t-norm or
or  tautologies. The set of all
tautologies. The set of all  tautologies is called the logic of the t-norm
tautologies is called the logic of the t-norm  since these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formula
since these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formula
e. Some formulae are tautologies with respect to all left-continuous t-norms: they represent general laws of propositional fuzzy logic which are independent of the choice of a particular left-continuous t-norm. These formulae form the logic MTL, which can thus be characterized as the logic of left-continuous t-norms.
s and the following primitive logical connective
s:
The following are the most common defined logical connectives:
Well-formed formula
e of MTL are defined as usual in propositional logics. In order to save parentheses, it is common to use the following order of precedence:
for MTL has been introduced by Esteva and Godo (2001). Its single derivation rule is modus ponens
:
The following are its axiom schemata: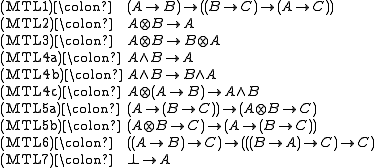
The traditional numbering of axioms, given in the left column, is derived from the numbering of axioms of Hájek's basic fuzzy logic BL. The axioms (MTL4a)–(MTL4c) replace the axiom of divisibility (BL4) of BL. The axioms (MTL5a) and (MTL5b) express the law of residuation
and the axiom (MTL6) corresponds to the condition of prelinearity. The axioms (MTL2) and (MTL3) of the original axiomatic system were shown to be redundant (Chvalovský, 2008) and (Cintula, 2005). All the other axioms were shown to be independent (Chvalovský, 2008).
, algebraic semantics
is predominantly used for MTL, with three main classes of algebras
with respect to which the logic is complete
:
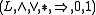 is an MTL-algebra if
is an MTL-algebra if
Important examples of MTL algebras are standard MTL-algebras on the real unit interval [0, 1]. Further examples include all Boolean algebras, all linear Heyting algebra
s (both with ), all MV-algebra
), all MV-algebra
s, all BL
-algebras, etc. Since the residuation condition can equivalently be expressed by identities, MTL-algebras form a variety
.
With this interpretation of connectives, any evaluation ev of propositional variables in L uniquely extends to an evaluation e of all well-formed formulae of MTL, by the following inductive definition (which generalizes Tarski's truth conditions
), for any formulae A, B, and any propositional variable p: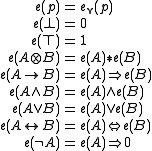
Informally, the truth value 1 represents full truth and the truth value 0 represents full falsity; intermediate truth values represent intermediate degrees of truth. Thus a formula is considered fully true under an evaluation e if e(A) = 1. A formula A is said to be valid in an MTL-algebra L if it is fully true under all evaluations in L, that is, if e(A) = 1 for all evaluations e in L. Some formulae (for instance, p → p) are valid in any MTL-algebra; these are called tautologies of MTL.
The notion of global entailment
(or: global consequence) is defined for MTL as follows: a set of formulae Γ entails a formula A (or: A is a global consequence of Γ), in symbols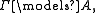 if for any evaluation e in any MTL-algebra, whenever e(B) = 1 for all formulae B in Γ, then also e(A) = 1. Informally, the global consequence relation represents the transmission of full truth in any MTL-algebra of truth values.
if for any evaluation e in any MTL-algebra, whenever e(B) = 1 for all formulae B in Γ, then also e(A) = 1. Informally, the global consequence relation represents the transmission of full truth in any MTL-algebra of truth values.
with respect to the class of all MTL-algebras (Esteva & Godo, 2001):
The notion of MTL-algebra is in fact so defined that MTL-algebras form the class of all algebras for which the logic MTL is sound. Furthermore, the strong completeness theorem holds:
(A subdirect product is a subalgebra of the direct product
such that all projection maps
are surjective
. An MTL-algebra is linearly ordered if its lattice order
is linear
.)
In consequence of the linear subdirect decomposition property of all MTL-algebras, the completeness theorem with respect to linear MTL-algebras (Esteva & Godo, 2001) holds:
 . The standard MTL-algebra determined by a left-continuous t-norm
. The standard MTL-algebra determined by a left-continuous t-norm  is usually denoted by
is usually denoted by 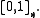 In
In 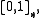 implication is represented by the residuum of
implication is represented by the residuum of 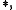 weak conjunction and disjunction respectively by the minimum and maximum, and the truth constants zero and one respectively by the real numbers 0 and 1.
weak conjunction and disjunction respectively by the minimum and maximum, and the truth constants zero and one respectively by the real numbers 0 and 1.
The logic MTL is complete with respect to standard MTL-algebras; this fact is expressed by the standard completeness theorem (Jenei & Montagna, 2002):
Since MTL is complete with respect to standard MTL-algebras, which are determined by left-continuous t-norms, MTL is often referred to as the logic of left-continuous t-norms (similarly as BL
is the logic of continuous t-norms).
T-norm
In mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
s, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logic
Substructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
s, or logics of residuated lattice
Residuated lattice
In abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
s; it extends the logic of commutative bounded integral residuated lattices (known as Höhle's monoidal logic, Ono's FLew, or intuitionistic logic without contraction) by the axiom of prelinearity.
Motivation
T-normT-norm
In mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
s are binary functions on the real unit interval [0, 1] which are often used to represent a conjunction connective in fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
. Every left-continuous t-norm
 has a unique residuum, that is, a function
has a unique residuum, that is, a function 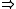 such that for all x, y, and z,
such that for all x, y, and z,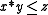 if and only if
if and only if 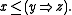
The residuum of a left-continuous t-norm can explicitly be defined as

This ensures that the residuum is the largest function such that for all x and y,
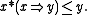
The latter can be interpreted as a fuzzy version of the modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
rule of inference. The residuum of a left-continuous t-norm thus can be characterized as the weakest function that makes the fuzzy modus ponens valid, which makes it a suitable truth function for implication in fuzzy logic. Left-continuity of the t-norm is the necessary and sufficient condition for this relationship between a t-norm conjunction and its residual implication to hold.
Truth functions of further propositional connectives can be defined by means of the t-norm and its residuum, for instance the residual negation
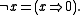 In this way, the left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives (see the section Standard semantics below) determine the truth values of complex propositional formula
In this way, the left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives (see the section Standard semantics below) determine the truth values of complex propositional formulaPropositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
e in [0, 1]. Formulae that always evaluate to 1 are then called tautologies
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
with respect to the given left-continuous t-norm
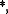 or
or  tautologies. The set of all
tautologies. The set of all  tautologies is called the logic of the t-norm
tautologies is called the logic of the t-norm 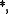 since these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formula
since these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formulaAtomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
e. Some formulae are tautologies with respect to all left-continuous t-norms: they represent general laws of propositional fuzzy logic which are independent of the choice of a particular left-continuous t-norm. These formulae form the logic MTL, which can thus be characterized as the logic of left-continuous t-norms.
Language
The language of the propositional logic MTL consists of countably many propositional variablePropositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
s and the following primitive logical connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s:
- Implication
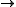 (binaryArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
(binaryArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
) - Strong conjunction
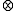 (binary). The sign & is a more traditional notation for strong conjunction in the literature on fuzzy logic, while the notation
(binary). The sign & is a more traditional notation for strong conjunction in the literature on fuzzy logic, while the notation 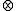 follows the tradition of substructural logics.
follows the tradition of substructural logics. - Weak conjunction
 (binary), also called lattice conjunction (as it is always realized by the latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
(binary), also called lattice conjunction (as it is always realized by the latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
operation of meetMeet (mathematics)In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
in algebraic semantics). Unlike BL and stronger fuzzy logics, weak conjunction is not definable in MTL and has to be included among primitive connectives. - Bottom
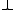 (nullary — a propositional constant);
(nullary — a propositional constant); 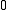 or
or 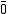 are common alternative signs and zero a common alternative name for the propositional constant (as the constants bottom and zero of substructural logics coincide in MTL).
are common alternative signs and zero a common alternative name for the propositional constant (as the constants bottom and zero of substructural logics coincide in MTL).
The following are the most common defined logical connectives:
- Negation
 (unaryUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
(unaryUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
), defined as
-
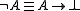
- Equivalence
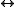 (binary), defined as
(binary), defined as
- Equivalence
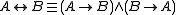
- In MTL, the definition is equivalent to
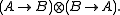
- (Weak) disjunction
 (binary), also called lattice disjunction (as it is always realized by the latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
(binary), also called lattice disjunction (as it is always realized by the latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
operation of join in algebraic semantics), defined as
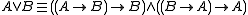
- Top
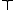 (nullary), also called one and denoted by
(nullary), also called one and denoted by 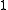 or
or 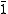 (as the constants top and zero of substructural logics coincide in MTL), defined as
(as the constants top and zero of substructural logics coincide in MTL), defined as
- Top
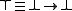
- (Weak) disjunction
Well-formed formula
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
e of MTL are defined as usual in propositional logics. In order to save parentheses, it is common to use the following order of precedence:
- Unary connectives (bind most closely)
- Binary connectives other than implication and equivalence
- Implication and equivalence (bind most loosely)
Axioms
A Hilbert-style deduction systemHilbert-style deduction system
In logic, especially mathematical logic, a Hilbert system, sometimes called Hilbert calculus or Hilbert–Ackermann system, is a type of system of formal deduction attributed to Gottlob Frege and David Hilbert...
for MTL has been introduced by Esteva and Godo (2001). Its single derivation rule is modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
:
- from
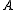 and
and 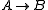 derive
derive 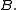
The following are its axiom schemata:
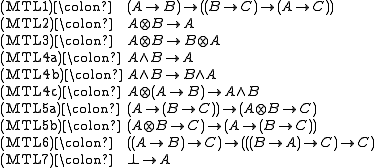
The traditional numbering of axioms, given in the left column, is derived from the numbering of axioms of Hájek's basic fuzzy logic BL. The axioms (MTL4a)–(MTL4c) replace the axiom of divisibility (BL4) of BL. The axioms (MTL5a) and (MTL5b) express the law of residuation
Residuated lattice
In abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
and the axiom (MTL6) corresponds to the condition of prelinearity. The axioms (MTL2) and (MTL3) of the original axiomatic system were shown to be redundant (Chvalovský, 2008) and (Cintula, 2005). All the other axioms were shown to be independent (Chvalovský, 2008).
Semantics
Like in other propositional t-norm fuzzy logicsT-norm fuzzy logics
T-norm fuzzy logics are a family of non-classical logics, informally delimited by having a semantics which takes the real unit interval [0, 1] for the system of truth values and functions called t-norms for permissible interpretations of conjunction...
, algebraic semantics
Algebraic semantics
An programming language theory, the algebraic semantics of a programming language is a form of axiomatic semantics based on algebraic laws for describing and reasoning about program semantics in a formal manner....
is predominantly used for MTL, with three main classes of algebras
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
with respect to which the logic is complete
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
:
- General semantics, formed of all MTL-algebras — that is, all algebras for which the logic is sound
- Linear semantics, formed of all linear MTL-algebras — that is, all MTL-algebras whose latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
order is linearTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total... - Standard semantics, formed of all standard MTL-algebras — that is, all MTL-algebras whose lattice reduct is the real unit interval [0, 1] with the usual order; they are uniquely determined by the function that interprets strong conjunction, which can be any left-continuous t-normT-normIn mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
MTL-algebras
Algebras for which the logic MTL is sound are called MTL-algebras. They can be characterized as prelinear commutative bounded integral residuated lattices. In more detail, an algebraic structure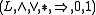 is an MTL-algebra if
is an MTL-algebra if
-
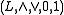 is a bounded latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
is a bounded latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
with the top element 0 and bottom element 1 -
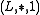 is a commutativeCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
is a commutativeCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for... -
 and
and 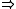 form an adjoint pairGalois connectionIn mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
form an adjoint pairGalois connectionIn mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
, that is,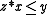 if and only if
if and only if 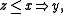 where
where 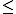 is the lattice order of
is the lattice order of 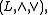 for all x, y, and z in
for all x, y, and z in 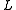 , (the residuation condition)
, (the residuation condition) -
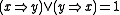 holds for all x and y in L (the prelinearity condition)
holds for all x and y in L (the prelinearity condition)
Important examples of MTL algebras are standard MTL-algebras on the real unit interval [0, 1]. Further examples include all Boolean algebras, all linear Heyting algebra
Heyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
s (both with
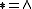 ), all MV-algebra
), all MV-algebraMV-algebra
In abstract algebra, a branch of pure mathematics, an MV-algebra is an algebraic structure with a binary operation \oplus, a unary operation \neg, and the constant 0, satisfying certain axioms...
s, all BL
BL (logic)
Basic fuzzy Logic , the logic of continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of all left-continuous t-norms MTL....
-algebras, etc. Since the residuation condition can equivalently be expressed by identities, MTL-algebras form a variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
.
Interpretation of the logic MTL in MTL-algebras
The connectives of MTL are interpreted in MTL-algebras as follows:- Strong conjunction by the monoidal operation

- Implication by the operation
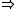 (which is called the residuum of
(which is called the residuum of  )
) - Weak conjunction and weak disjunction by the lattice operations
 and
and 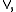 respectively (usually denoted by the same symbols as the connectives, if no confusion can arise)
respectively (usually denoted by the same symbols as the connectives, if no confusion can arise) - The truth constants zero (top) and one (bottom) by the constants 0 and 1
- The equivalence connective is interpreted by the operation
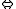 defined as
defined as
-
- Due to the prelinearity condition, this definition is equivalent to one that uses
 instead of
instead of 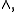 thus
thus
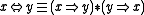
- Negation is interpreted by the definable operation
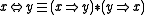
- Negation is interpreted by the definable operation
With this interpretation of connectives, any evaluation ev of propositional variables in L uniquely extends to an evaluation e of all well-formed formulae of MTL, by the following inductive definition (which generalizes Tarski's truth conditions
Semantic theory of truth
A semantic theory of truth is a theory of truth in the philosophy of language which holds that truth is a property of sentences.-Origin:The semantic conception of truth, which is related in different ways to both the correspondence and deflationary conceptions, is due to work published by Polish...
), for any formulae A, B, and any propositional variable p:
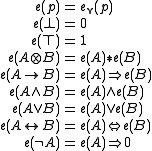
Informally, the truth value 1 represents full truth and the truth value 0 represents full falsity; intermediate truth values represent intermediate degrees of truth. Thus a formula is considered fully true under an evaluation e if e(A) = 1. A formula A is said to be valid in an MTL-algebra L if it is fully true under all evaluations in L, that is, if e(A) = 1 for all evaluations e in L. Some formulae (for instance, p → p) are valid in any MTL-algebra; these are called tautologies of MTL.
The notion of global entailment
Entailment
In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
(or: global consequence) is defined for MTL as follows: a set of formulae Γ entails a formula A (or: A is a global consequence of Γ), in symbols
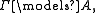 if for any evaluation e in any MTL-algebra, whenever e(B) = 1 for all formulae B in Γ, then also e(A) = 1. Informally, the global consequence relation represents the transmission of full truth in any MTL-algebra of truth values.
if for any evaluation e in any MTL-algebra, whenever e(B) = 1 for all formulae B in Γ, then also e(A) = 1. Informally, the global consequence relation represents the transmission of full truth in any MTL-algebra of truth values.General soundness and completeness theorems
The logic MTL is sound and completeCompleteness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
with respect to the class of all MTL-algebras (Esteva & Godo, 2001):
- A formula is provable in MTL if and only if it is valid in all MTL-algebras.
The notion of MTL-algebra is in fact so defined that MTL-algebras form the class of all algebras for which the logic MTL is sound. Furthermore, the strong completeness theorem holds:
- A formula A is a global consequence in MTL of a set of formulae Γ if and only if A is derivable from Γ in MTL.
Linear semantics
Like algebras for other fuzzy logics, MTL-algebras enjoy the following linear subdirect decomposition property:- Every MTL-algebra is a subdirect product of linearly ordered MTL-algebras.
(A subdirect product is a subalgebra of the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
such that all projection maps
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
are surjective
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
. An MTL-algebra is linearly ordered if its lattice order
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
is linear
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
.)
In consequence of the linear subdirect decomposition property of all MTL-algebras, the completeness theorem with respect to linear MTL-algebras (Esteva & Godo, 2001) holds:
- A formula is provable in MTL if and only if it is valid in all linear MTL-algebras.
- A formula A is derivable in MTL from a set of formulae Γ if and only if A is a global consequence in all linear MTL-algebras of Γ.
Standard semantics
Standard are called those MTL-algebras whose lattice reduct is the real unit interval [0, 1]. They are uniquely determined by the real-valued function that interprets strong conjunction, which can be any left-continuous t-normT-norm
In mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
 . The standard MTL-algebra determined by a left-continuous t-norm
. The standard MTL-algebra determined by a left-continuous t-norm  is usually denoted by
is usually denoted by 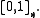 In
In 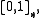 implication is represented by the residuum of
implication is represented by the residuum of 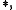 weak conjunction and disjunction respectively by the minimum and maximum, and the truth constants zero and one respectively by the real numbers 0 and 1.
weak conjunction and disjunction respectively by the minimum and maximum, and the truth constants zero and one respectively by the real numbers 0 and 1.The logic MTL is complete with respect to standard MTL-algebras; this fact is expressed by the standard completeness theorem (Jenei & Montagna, 2002):
- A formula is provable in MTL if and only if it is valid in all standard MTL-algebras.
Since MTL is complete with respect to standard MTL-algebras, which are determined by left-continuous t-norms, MTL is often referred to as the logic of left-continuous t-norms (similarly as BL
BL (logic)
Basic fuzzy Logic , the logic of continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of all left-continuous t-norms MTL....
is the logic of continuous t-norms).