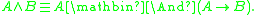T-norm fuzzy logics
Encyclopedia
T-norm fuzzy logics are a family of non-classical logic
s, informally delimited by having a semantics which takes the real unit interval [0, 1] for the system of truth values and functions called t-norm
s for permissible interpretations of conjunction
. They are mainly used in applied fuzzy logic
and fuzzy set theory
as a theoretical basis for approximate reasoning.
T-norm fuzzy logics belong in broader classes of fuzzy logic
s and many-valued logics. In order to generate a well-behaved implication, the t-norms are usually required to be left-continuous; logics of left-continuous t-norms further belong in the class of substructural logic
s, among which they are marked with the validity of the law of prelinearity, (A → B) ∨ (B → A). Both propositional and first-order
(or higher-order
) t-norm fuzzy logics, as well as their expansions by modal and other operators, are studied. Logics which restrict the t-norm semantics to a subset of the real unit interval (for example, finitely valued Łukasiewicz logics) are usually included in the class as well.
Important examples of t-norm fuzzy logics are monoidal t-norm logic MTL
of all left-continuous t-norms, basic logic BL
of all continuous t-norms, product fuzzy logic of the product t-norm, or the nilpotent minimum logic of the nilpotent minimum t-norm. Some independently motivated logics belong among t-norm fuzzy logics, too, for example Łukasiewicz logic (which is the logic of the Łukasiewicz t-norm) or Gödel–Dummett logic
(which is the logic of the minimum t-norm).
s, t-norm fuzzy logics primarily aim at generalizing classical two-valued logic by admitting intermediary truth values between 1 (truth) and 0 (falsity) representing degrees of truth of propositions. The degrees are assumed to be real numbers from the unit interval [0, 1]. In propositional t-norm fuzzy logics, propositional connectives
are stipulated to be truth-functional, that is, the truth value of a complex proposition formed by a propositional connective from some constituent propositions is a function (called the truth function of the connective) of the truth values of the constituent propositions. The truth functions operate on the set of truth degrees (in the standard semantics, on the [0, 1] interval); thus the truth function of an n-ary propositional connective c is a function Fc: [0, 1]n → [0, 1]. Truth functions generalize truth table
s of propositional connectives known from classical logic to operate on the larger system of truth values.
T-norm fuzzy logics impose certain natural constraints on the truth function of conjunction
. The truth function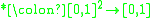 of conjunction is assumed to satisfy the following conditions:
of conjunction is assumed to satisfy the following conditions:
These assumptions make the truth function of conjunction a left-continuous t-norm
, which explains the name of the family of fuzzy logics (t-norm based). Particular logics of the family can make further assumptions about the behavior of conjunction (for example, Gödel logic
requires its idempotence
) or other connectives (for example, the logic IMTL requires the involutiveness
of negation).
All left-continuous t-norms have a unique residuum, that is, a binary function
have a unique residuum, that is, a binary function 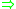 such that for all x, y, and z in [0, 1],
such that for all x, y, and z in [0, 1],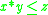 if and only if
if and only if 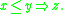
The residuum of a left-continuous t-norm can explicitly be defined as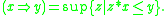
This ensures that the residuum is the pointwise largest function such that for all x and y,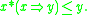
The latter can be interpreted as a fuzzy version of the modus ponens
rule of inference. The residuum of a left-continuous t-norm thus can be characterized as the weakest function that makes the fuzzy modus ponens valid, which makes it a suitable truth function for implication in fuzzy logic. Left-continuity of the t-norm is the necessary and sufficient condition for this relationship between a t-norm conjunction and its residual implication to hold.
Truth functions of further propositional connectives can be defined by means of the t-norm and its residuum, for instance the residual negation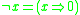 or bi-residual equivalence
or bi-residual equivalence  Truth functions of propositional connectives may also be introduced by additional definitions: the most usual ones are the minimum (which plays a role of another conjunctive connective), the maximum (which plays a role of a disjunctive connective), or the Baaz Delta operator, defined in [0, 1] as
Truth functions of propositional connectives may also be introduced by additional definitions: the most usual ones are the minimum (which plays a role of another conjunctive connective), the maximum (which plays a role of a disjunctive connective), or the Baaz Delta operator, defined in [0, 1] as 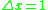 if
if 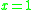 and
and 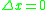 otherwise. In this way, a left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives determine the truth values of complex propositional formulae in [0, 1].
otherwise. In this way, a left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives determine the truth values of complex propositional formulae in [0, 1].
Formulae that always evaluate to 1 are called tautologies with respect to the given left-continuous t-norm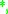 or
or  tautologies. The set of all
tautologies. The set of all  tautologies is called the logic of the t-norm
tautologies is called the logic of the t-norm 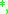 as these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formula
as these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formula
e. Some formulae are tautologies
with respect to a larger class of left-continuous t-norms; the set of such formulae is called the logic of the class. Important t-norm logics are the logics of particular t-norms or classes of t-norms, for example:
It turns out that many logics of particular t-norms and classes of t-norms are axiomatizable. The completeness theorem of the axiomatic system with respect to the corresponding t-norm semantics on [0, 1] is then called the standard completeness of the logic. Besides the standard real-valued semantics on [0, 1], the logics are sound and complete with respect to general algebraic semantics, formed by suitable classes of prelinear commutative bounded integral residuated lattice
s.
or t-norm
emerged):
A systematic study of particular t-norm fuzzy logics and their classes began with Hájek
's (1998) monograph Metamathematics of Fuzzy Logic, which presented the notion of the logic of a continuous t-norm, the logics of the three basic continuous t-norms (Łukasiewicz, Gödel, and product), and the 'basic' fuzzy logic BL
of all continuous t-norms (all of them both propositional and first-order). The book also started the investigation of fuzzy logics as non-classical logics with Hilbert-style calculi, algebraic semantics, and metamathematical properties known from other logics (completeness theorems, deduction theorems, complexity, etc.).
Since then, a plethora of t-norm fuzzy logics have been introduced and their metamathematical properties have been investigated. Some of the most important t-norm fuzzy logics were introduced in 2001, by Esteva and Godo (MTL
, IMTL, SMTL, NM, WNM), Esteva, Godo, and Montagna (propositional ŁΠ), and Cintula (first-order ŁΠ).
Some propositional t-norm logics add further propositional connectives to the above language, most often the following ones:
Well-formed formula
e of propositional t-norm logics are defined from propositional variable
s (usually countably many) by the above logical connectives, as usual in propositional logics. In order to save parentheses, it is common to use the following order of precedence:
First-order variants of t-norm logics employ the usual logical language of first-order logic
with the above propositional connectives and the following quantifiers:
The first-order variant of a propositional t-norm logic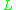 is usually denoted by
is usually denoted by 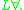
is predominantly used for propositional t-norm fuzzy logics, with three main classes of algebras
with respect to which a t-norm fuzzy logic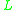 is complete
is complete
:
Non-classical logic
Non-classical logics is the name given to formal systems which differ in a significant way from standard logical systems such as propositional and predicate logic. There are several ways in which this is done, including by way of extensions, deviations, and variations...
s, informally delimited by having a semantics which takes the real unit interval [0, 1] for the system of truth values and functions called t-norm
T-norm
In mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
s for permissible interpretations of conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
. They are mainly used in applied fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
and fuzzy set theory
Fuzzy set
Fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced simultaneously by Lotfi A. Zadeh and Dieter Klaua in 1965 as an extension of the classical notion of set. In classical set theory, the membership of elements in a set is assessed in binary terms according to...
as a theoretical basis for approximate reasoning.
T-norm fuzzy logics belong in broader classes of fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
s and many-valued logics. In order to generate a well-behaved implication, the t-norms are usually required to be left-continuous; logics of left-continuous t-norms further belong in the class of substructural logic
Substructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
s, among which they are marked with the validity of the law of prelinearity, (A → B) ∨ (B → A). Both propositional and first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
(or higher-order
Higher-order logic
In mathematics and logic, a higher-order logic is a form of predicate logic that is distinguished from first-order logic by additional quantifiers and a stronger semantics...
) t-norm fuzzy logics, as well as their expansions by modal and other operators, are studied. Logics which restrict the t-norm semantics to a subset of the real unit interval (for example, finitely valued Łukasiewicz logics) are usually included in the class as well.
Important examples of t-norm fuzzy logics are monoidal t-norm logic MTL
Monoidal t-norm logic
Monoidal t-norm based logic , the logic of left-continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of commutative bounded integral residuated lattices by the axiom of...
of all left-continuous t-norms, basic logic BL
BL (logic)
Basic fuzzy Logic , the logic of continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of all left-continuous t-norms MTL....
of all continuous t-norms, product fuzzy logic of the product t-norm, or the nilpotent minimum logic of the nilpotent minimum t-norm. Some independently motivated logics belong among t-norm fuzzy logics, too, for example Łukasiewicz logic (which is the logic of the Łukasiewicz t-norm) or Gödel–Dummett logic
Intermediate logic
In mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
(which is the logic of the minimum t-norm).
Motivation
As members of the family of fuzzy logicFuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
s, t-norm fuzzy logics primarily aim at generalizing classical two-valued logic by admitting intermediary truth values between 1 (truth) and 0 (falsity) representing degrees of truth of propositions. The degrees are assumed to be real numbers from the unit interval [0, 1]. In propositional t-norm fuzzy logics, propositional connectives
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
are stipulated to be truth-functional, that is, the truth value of a complex proposition formed by a propositional connective from some constituent propositions is a function (called the truth function of the connective) of the truth values of the constituent propositions. The truth functions operate on the set of truth degrees (in the standard semantics, on the [0, 1] interval); thus the truth function of an n-ary propositional connective c is a function Fc: [0, 1]n → [0, 1]. Truth functions generalize truth table
Truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
s of propositional connectives known from classical logic to operate on the larger system of truth values.
T-norm fuzzy logics impose certain natural constraints on the truth function of conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
. The truth function
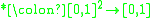 of conjunction is assumed to satisfy the following conditions:
of conjunction is assumed to satisfy the following conditions:
- Commutativity, that is,
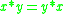 for all x and y in [0, 1]. This expresses the assumption that the order of fuzzy propositions is immaterial in conjunction, even if intermediary truth degrees are admitted.
for all x and y in [0, 1]. This expresses the assumption that the order of fuzzy propositions is immaterial in conjunction, even if intermediary truth degrees are admitted. - Associativity, that is,
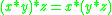 for all x, y, and z in [0, 1]. This expresses the assumption that the order of performing conjunction is immaterial, even if intermediary truth degrees are admitted.
for all x, y, and z in [0, 1]. This expresses the assumption that the order of performing conjunction is immaterial, even if intermediary truth degrees are admitted. - Monotony, that is, if
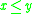 then
then 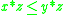 for all x, y, and z in [0, 1]. This expresses the assumption that increasing the truth degree of a conjunct should not decrease the truth degree of the conjunction.
for all x, y, and z in [0, 1]. This expresses the assumption that increasing the truth degree of a conjunct should not decrease the truth degree of the conjunction. - Neutrality of 1, that is,
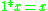 for all x in [0, 1]. This assumption corresponds to regarding the truth degree 1 as full truth, conjunction with which does not decrease the truth value of the other conjunct. Together with the previous conditions this condition ensures that also
for all x in [0, 1]. This assumption corresponds to regarding the truth degree 1 as full truth, conjunction with which does not decrease the truth value of the other conjunct. Together with the previous conditions this condition ensures that also 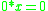 for all x in [0, 1], which corresponds to regarding the truth degree 0 as full falsity, conjunction with which is always fully false.
for all x in [0, 1], which corresponds to regarding the truth degree 0 as full falsity, conjunction with which is always fully false. - Continuity of the function
 (the previous conditions reduce this requirement to the continuity in either argument). Informally this expresses the assumption that microscopic changes of the truth degrees of conjuncts should not result in a macroscopic change of the truth degree of their conjunction. This condition, among other things, ensures a good behavior of (residual) implication derived from conjunction; to ensure the good behavior, however, left-continuity (in either argument) of the function
(the previous conditions reduce this requirement to the continuity in either argument). Informally this expresses the assumption that microscopic changes of the truth degrees of conjuncts should not result in a macroscopic change of the truth degree of their conjunction. This condition, among other things, ensures a good behavior of (residual) implication derived from conjunction; to ensure the good behavior, however, left-continuity (in either argument) of the function  is sufficient. In general t-norm fuzzy logics, therefore, only left-continuity of
is sufficient. In general t-norm fuzzy logics, therefore, only left-continuity of  is required, which expresses the assumption that a microscopic decrease of the truth degree of a conjunct should not macroscopically decrease the truth degree of conjunction.
is required, which expresses the assumption that a microscopic decrease of the truth degree of a conjunct should not macroscopically decrease the truth degree of conjunction.
These assumptions make the truth function of conjunction a left-continuous t-norm
T-norm
In mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
, which explains the name of the family of fuzzy logics (t-norm based). Particular logics of the family can make further assumptions about the behavior of conjunction (for example, Gödel logic
Intermediate logic
In mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
requires its idempotence
Idempotence
Idempotence is the property of certain operations in mathematics and computer science, that they can be applied multiple times without changing the result beyond the initial application...
) or other connectives (for example, the logic IMTL requires the involutiveness
Involution
In mathematics, an involution, or an involutary function, is a function f that is its own inverse:-General properties:Any involution is a bijection.The identity map is a trivial example of an involution...
of negation).
All left-continuous t-norms
 have a unique residuum, that is, a binary function
have a unique residuum, that is, a binary function 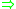 such that for all x, y, and z in [0, 1],
such that for all x, y, and z in [0, 1],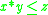 if and only if
if and only if 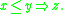
The residuum of a left-continuous t-norm can explicitly be defined as
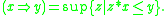
This ensures that the residuum is the pointwise largest function such that for all x and y,
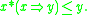
The latter can be interpreted as a fuzzy version of the modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
rule of inference. The residuum of a left-continuous t-norm thus can be characterized as the weakest function that makes the fuzzy modus ponens valid, which makes it a suitable truth function for implication in fuzzy logic. Left-continuity of the t-norm is the necessary and sufficient condition for this relationship between a t-norm conjunction and its residual implication to hold.
Truth functions of further propositional connectives can be defined by means of the t-norm and its residuum, for instance the residual negation
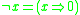 or bi-residual equivalence
or bi-residual equivalence  Truth functions of propositional connectives may also be introduced by additional definitions: the most usual ones are the minimum (which plays a role of another conjunctive connective), the maximum (which plays a role of a disjunctive connective), or the Baaz Delta operator, defined in [0, 1] as
Truth functions of propositional connectives may also be introduced by additional definitions: the most usual ones are the minimum (which plays a role of another conjunctive connective), the maximum (which plays a role of a disjunctive connective), or the Baaz Delta operator, defined in [0, 1] as 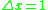 if
if 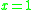 and
and 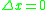 otherwise. In this way, a left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives determine the truth values of complex propositional formulae in [0, 1].
otherwise. In this way, a left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives determine the truth values of complex propositional formulae in [0, 1].Formulae that always evaluate to 1 are called tautologies with respect to the given left-continuous t-norm
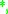 or
or  tautologies. The set of all
tautologies. The set of all  tautologies is called the logic of the t-norm
tautologies is called the logic of the t-norm 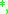 as these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formula
as these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formulaAtomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
e. Some formulae are tautologies
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
with respect to a larger class of left-continuous t-norms; the set of such formulae is called the logic of the class. Important t-norm logics are the logics of particular t-norms or classes of t-norms, for example:
- Łukasiewicz logic is the logic of the Łukasiewicz t-norm
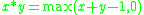
- Gödel–Dummett logicIntermediate logicIn mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
is the logic of the minimum t-norm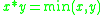
- Product fuzzy logic is the logic of the product t-norm
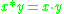
- Monoidal t-norm logicMonoidal t-norm logicMonoidal t-norm based logic , the logic of left-continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of commutative bounded integral residuated lattices by the axiom of...
MTL is the logic of (the class of) all left-continuous t-norms - Basic fuzzy logic BL is the logic of (the class of) all continuous t-norms
It turns out that many logics of particular t-norms and classes of t-norms are axiomatizable. The completeness theorem of the axiomatic system with respect to the corresponding t-norm semantics on [0, 1] is then called the standard completeness of the logic. Besides the standard real-valued semantics on [0, 1], the logics are sound and complete with respect to general algebraic semantics, formed by suitable classes of prelinear commutative bounded integral residuated lattice
Residuated lattice
In abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
s.
History
Some particular t-norm fuzzy logics have been introduced and investigated long before the family was recognized (even before the notions of fuzzy logicFuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
or t-norm
T-norm
In mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
emerged):
- Łukasiewicz logic (the logic of the Łukasiewicz t-norm) was originally defined by Jan Łukasiewicz (1920) as a three-valued logic; it was later generalized to n-valued (for all finite n) as well as infinitely-many-valued variants, both propositional and first-order.
- Gödel–Dummett logicIntermediate logicIn mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
(the logic of the minimum t-norm) was implicit in GödelGodelGodel or similar can mean:*Kurt Gödel , an Austrian logician, mathematician and philosopher*Gödel...
's 1932 proof of infinite-valuedness of intuitionistic logicIntuitionistic logicIntuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
. Later (1959) it was explicitly studied by DummettMichael DummettSir Michael Anthony Eardley Dummett FBA D.Litt is a British philosopher. He was, until 1992, Wykeham Professor of Logic at the University of Oxford...
who proved a completeness theorem for the logic.
A systematic study of particular t-norm fuzzy logics and their classes began with Hájek
Petr Hájek
Petr Hájek is a Czech scientist in the area of mathematical logic and a professor of mathematics. He works at the Institute of Computer Science at the Academy of Sciences of the Czech Republic and worked as a lecturer at the Faculty of Mathematics and Physics at the Charles University in Prague...
's (1998) monograph Metamathematics of Fuzzy Logic, which presented the notion of the logic of a continuous t-norm, the logics of the three basic continuous t-norms (Łukasiewicz, Gödel, and product), and the 'basic' fuzzy logic BL
BL (logic)
Basic fuzzy Logic , the logic of continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of all left-continuous t-norms MTL....
of all continuous t-norms (all of them both propositional and first-order). The book also started the investigation of fuzzy logics as non-classical logics with Hilbert-style calculi, algebraic semantics, and metamathematical properties known from other logics (completeness theorems, deduction theorems, complexity, etc.).
Since then, a plethora of t-norm fuzzy logics have been introduced and their metamathematical properties have been investigated. Some of the most important t-norm fuzzy logics were introduced in 2001, by Esteva and Godo (MTL
Monoidal t-norm logic
Monoidal t-norm based logic , the logic of left-continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of commutative bounded integral residuated lattices by the axiom of...
, IMTL, SMTL, NM, WNM), Esteva, Godo, and Montagna (propositional ŁΠ), and Cintula (first-order ŁΠ).
Logical language
The logical vocabulary of propositional t-norm fuzzy logics standardly comprises the following connectives:- Implication
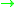 (binaryArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
(binaryArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
). In the context of other than t-norm-based fuzzy logics, the t-norm-based implication is sometimes called residual implication or R-implication, as its standard semantics is the residuum of the t-normT-normIn mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
that realizes strong conjunction. - Strong conjunction
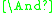 (binary). In the context of substructural logics, the sign
(binary). In the context of substructural logics, the sign  and the names group, intensional, multiplicative, or parallel conjunction are often used for strong conjunction.
and the names group, intensional, multiplicative, or parallel conjunction are often used for strong conjunction. - Weak conjunction
 (binary), also called lattice conjunction (as it is always realized by the latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
(binary), also called lattice conjunction (as it is always realized by the latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
operation of meetMeet (mathematics)In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
in algebraic semantics). In the context of substructural logics, the names additive, extensional, or comparative conjunction are sometimes used for lattice conjunction. In the logic BLBL (logic)Basic fuzzy Logic , the logic of continuous t-norms, is one of t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of all left-continuous t-norms MTL....
and its extensions (though not in t-norm logics in general), weak conjunction is definable in terms of implication and strong conjunction, by
-
- The presence of two conjunction connectives is a common feature of contraction-free substructural logicSubstructural logicIn logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
s.- Bottom
 (nullary);
(nullary); 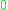 or
or 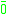 are common alternative signs and zero a common alternative name for the propositional constant (as the constants bottom and zero of substructural logics coincide in t-norm fuzzy logics). The proposition
are common alternative signs and zero a common alternative name for the propositional constant (as the constants bottom and zero of substructural logics coincide in t-norm fuzzy logics). The proposition  represents the falsity or absurdum and corresponds to the classical truth value false.
represents the falsity or absurdum and corresponds to the classical truth value false. - Negation
 (unaryUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
(unaryUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
), sometimes called residual negation if other negation connectives are considered, as it is defined from the residual implication by the reductio ad absurdum:
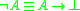
- Equivalence
 (binary), defined as
(binary), defined as
- Equivalence

- Bottom
- In t-norm logics, the definition is equivalent to
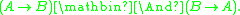
- (Weak) disjunction
 (binary), also called lattice disjunction (as it is always realized by the latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
(binary), also called lattice disjunction (as it is always realized by the latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
operation of join in algebraic semantics). In t-norm logics it is definable in terms of other connectives as
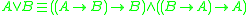
- Top
 (nullary), also called one and denoted by
(nullary), also called one and denoted by  or
or 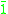 (as the constants top and zero of substructural logics coincide in t-norm fuzzy logics). The proposition
(as the constants top and zero of substructural logics coincide in t-norm fuzzy logics). The proposition  corresponds to the classical truth value true and can in t-norm logics be defined as
corresponds to the classical truth value true and can in t-norm logics be defined as
- Top
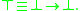
- (Weak) disjunction
Some propositional t-norm logics add further propositional connectives to the above language, most often the following ones:
- The Delta connective
 is a unary connective that asserts classical truth of a proposition, as the formulae of the form
is a unary connective that asserts classical truth of a proposition, as the formulae of the form 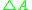 behave as in classical logic. Also called the Baaz Delta, as it was first used by Matthias Baaz for Gödel–Dummett logicIntermediate logicIn mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
behave as in classical logic. Also called the Baaz Delta, as it was first used by Matthias Baaz for Gödel–Dummett logicIntermediate logicIn mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
. The expansion of a t-norm logic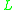 by the Delta connective is usually denoted by
by the Delta connective is usually denoted by 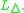
- Truth constants are nullary connectives representing particular truth values between 0 and 1 in the standard real-valued semantics. For the real number
 , the corresponding truth constant is usually denoted by
, the corresponding truth constant is usually denoted by  Most often, the truth constants for all rational numbers are added. The system of all truth constants in the language is supposed to satisfy the bookkeeping axioms:
Most often, the truth constants for all rational numbers are added. The system of all truth constants in the language is supposed to satisfy the bookkeeping axioms:
-
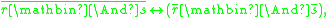
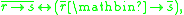 etc. for all propositional connectives and all truth constants definable in the language.
etc. for all propositional connectives and all truth constants definable in the language.
- Involutive negation
 (unary) can be added as an additional negation to t-norm logics whose residual negation is not itself involutive, that is, if it does not obey the law of double negation
(unary) can be added as an additional negation to t-norm logics whose residual negation is not itself involutive, that is, if it does not obey the law of double negation 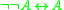 . A t-norm logic
. A t-norm logic 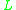 expanded with involutive negation is usually denoted by
expanded with involutive negation is usually denoted by 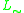 and called
and called 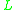 with involution.
with involution. - Strong disjunction
 (binary). In the context of substructural logics it is also called group, intensional, multiplicative, or parallel disjunction. Even though standard in contraction-free substructural logics, in t-norm fuzzy logics it is usually used only in the presence of involutive negation, which makes it definable (and so axiomatizable) by de Morgan's law from strong conjunction:
(binary). In the context of substructural logics it is also called group, intensional, multiplicative, or parallel disjunction. Even though standard in contraction-free substructural logics, in t-norm fuzzy logics it is usually used only in the presence of involutive negation, which makes it definable (and so axiomatizable) by de Morgan's law from strong conjunction:
- Involutive negation
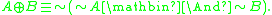
- Additional t-norm conjunctions and residual implications. Some expressively strong t-norm logics, for instance the logic ŁΠ, have more than one strong conjunction or residual implication in their language. In the standard real-valued semantics, all such strong conjunctions are realized by different t-norms and the residual implications by their residua.
Well-formed formula
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
e of propositional t-norm logics are defined from propositional variable
Propositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
s (usually countably many) by the above logical connectives, as usual in propositional logics. In order to save parentheses, it is common to use the following order of precedence:
- Unary connectives (bind most closely)
- Binary connectives other than implication and equivalence
- Implication and equivalence (bind most loosely)
First-order variants of t-norm logics employ the usual logical language of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with the above propositional connectives and the following quantifiers:
- General quantifier
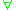
- Existential quantifier
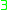
The first-order variant of a propositional t-norm logic
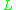 is usually denoted by
is usually denoted by 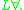
Semantics
Algebraic semanticsAlgebraic semantics
An programming language theory, the algebraic semantics of a programming language is a form of axiomatic semantics based on algebraic laws for describing and reasoning about program semantics in a formal manner....
is predominantly used for propositional t-norm fuzzy logics, with three main classes of algebras
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
with respect to which a t-norm fuzzy logic
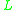 is complete
is completeCompleteness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
:
- General semantics, formed of all
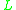 -algebras — that is, all algebras for which the logic is sound.
-algebras — that is, all algebras for which the logic is sound. - Linear semantics, formed of all linear
 -algebras — that is, all
-algebras — that is, all 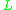 -algebras whose latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
-algebras whose latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
order is linearTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
. - Standard semantics, formed of all standard
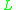 -algebras — that is, all
-algebras — that is, all 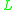 -algebras whose lattice reduct is the real unit interval [0, 1] with the usual order. In standard
-algebras whose lattice reduct is the real unit interval [0, 1] with the usual order. In standard 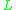 -algebras, the interpretation of strong conjunction is a left-continuous t-normT-normIn mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
-algebras, the interpretation of strong conjunction is a left-continuous t-normT-normIn mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic...
and the interpretation of most propositional connectives is determined by the t-norm (hence the names t-norm-based logics and t-norm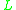 -algebras, which is also used for
-algebras, which is also used for 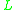 -algebras on the lattice [0, 1]). In t-norm logics with additional connectives, however, the real-valued interpretation of the additional connectives may be restricted by further conditions for the t-norm algebra to be called standard: for example, in standard
-algebras on the lattice [0, 1]). In t-norm logics with additional connectives, however, the real-valued interpretation of the additional connectives may be restricted by further conditions for the t-norm algebra to be called standard: for example, in standard 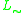 -algebras of the logic
-algebras of the logic 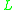 with involution, the interpretation of the additional involutive negation
with involution, the interpretation of the additional involutive negation  is required to be the standard involution
is required to be the standard involution 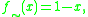 rather than other involutions which can also interpret
rather than other involutions which can also interpret  over t-norm
over t-norm  -algebras. In general, therefore, the definition of standard t-norm algebras has to be explicitly given for t-norm logics with additional connectives.
-algebras. In general, therefore, the definition of standard t-norm algebras has to be explicitly given for t-norm logics with additional connectives.