Entailment
Encyclopedia
In logic
, entailment is a relation between a set of sentences (e.g., meaningfully declarative sentences or truthbearer
s) and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction
of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent. S2 is called the logical consequent of Γ; S1 is said to logically imply S2.
Two sentences are inconsistent if and only if they cannot both be true; they are logically inconsistent if and only if they are inconsistent as a result of their logical form
.
Thus if
and
then Γ entails S2, because
and
are logically inconsistent. They are logically inconsistent because as a result of their logical form they cannot be both true, their logical forms being p and q and not-q.
On the other hand if
then Γ does not entail S2 because
andS2, “John is not a man”
are not logically inconsistent because they can both be true as a result of their logical form, their logical form being p and not-q.
Since
and
it follows that
It is therefore of the first importance to clarify the term logical form and explain how the logically relevant form(s) of a sentence can be established.
The logical form of sentences can be revealed by means of a formal language
enabling the following definition of entailment. Roughly, if S1 and S2 are interpretations of two sentences θ and ψ in a formal language of classical logic
, then S1 entails S2 if and only if not (θ and not ψ) is true under all interpretations
.
More precisely, if Γ is a set of one or more sentences and S1 is the conjunction of the elements of Γ and S2 is a sentence, Γ entails S2 if and only if not (S1 and not-S2) is a logical truth
. S2 is called the 'logical consequent' of Γ. S1 is said to 'logically imply' S2.
Not (S1 and not-S2) is a logical truth if θ and Ψ are closed well-formed formula
e (often denoted 'wff'), wffs (sentences) in a formal language L in classical logic, and I is an interpretation
of L, and θ is true under I if and only if S1 and Ψ is true under I if and only if S2, and not (θ and not Ψ) is logically valid
.
A closed wff Φ in L is 'logically valid' if and only if Φ is true under all interpretations of L. Hence
Thus if Γ = {“Roses are red”, “Violets are blue”}, S1=“Roses are red and Violets are blue” and S2 = “Violets are Blue” then Γ entails S2 because not(S1 and not-S2), “It is not the case that roses are red and violets are blue and violets are not blue” is a logical truth.
Not(S1 and not-S2) is a logical truth because there are two closed wfs, P&Q and Q in a formal language L in classical logic and there is an interpretation I of L, and P&Q is true under I if and only if roses are red and violets are blue, and Q is true under I if and only if violets are blue, and ¬((P&Q)&¬Q) is logically valid. ¬((P&Q)&¬Q)) is logically valid because it is true under all interpretations of L (note that ¬ means not
).
It will be noted that, on these definitions, if (i) S1 is inconsistent (self-contradictory) or (ii) not-S2 is inconsistent (self-contradictory) then (S1 and not-S2) is inconsistent (not consistent) and hence S1 entails S2.
Ideally, entailment and deduction
would be extension
ally equivalent. However, this is not always the case. In such a case, it is useful to break the equivalence down into its two parts:
A deductive system
S is complete for a language L if and only if
implies 
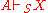: that is, if all valid
arguments are deducible (or provable), where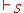
denotes the deducibility relation for the system S. NB 
means that X is provable from A for a language L, and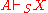 
means that X is a semantic consequence of A for the system S.
A deductive system S is sound
for a language L if and only if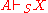
implies 
: that is, if no invalid arguments are provable.
Many introductory textbooks (e.g. Mendelson's "Introduction to Mathematical Logic") that introduce first-order logic, include a complete and sound inference system for the first-order logic. In contrast, second-order logic
— which allows quantification over predicates — does not have a complete and sound inference system with respect to a full Henkin
(or standard) semantics.
a proof that not (θ and not Ψ) is logically valid
would be a proof that Γ entails S2.
It can be easily demonstrated, for example by means of a truth-table, that ¬((P&Q)&¬Q) is a tautology
and hence true under all interpretations and hence logically valid. Moreover, if T is a consistent theory
in L and ¬(θ∧¬Ψ) is a theorem in T (written ⊢T¬(θ∧¬Ψ)) then ¬(θ∧¬Ψ) is logically valid and, consequently, all interpretations of ¬(θ∧¬Ψ) are logical truths, including not(S1 and not-S2). Hence Γ entails S2 if ⊢T¬(θ∧¬Ψ) and T is consistent.
S1 entails S2 if and only if:
FS of a set Г of formulas if there is a formal proof
in FS of A from the set Г.
Syntactic consequence does not depend on any interpretation
of the formal system.
,
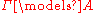if and only if no interpretation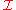
makes all members of Г true and A false. Or, in other words, the set of the interpretations that make all members of Г true is a subset of the set of the interpretations that make A true.
. Inductive reasoning
is another. Scientific method
involves inferences that are not solely entailment. Entailment does not encompass non-monotonic reasoning or defeasible reasoning
. See also
Alternatively (and, most would say, equivalently):
Such accounts are called "modal" because they appeal to the modal notions of necessity and (im)possibility
. 'It is necessary that' is often cashed out as a universal quantifier over possible worlds
, so that the accounts above translate as:
Consider the modal account in terms of the argument given as an example above:
The conclusion is a logical consequence of the premises because we can't imagine a possible world where (a) all frogs are green; (b) Kermit is a frog; and (c) Kermit is not green.
Most logicians would probably agree that logical consequence, as we intuitively understand it, has both a modal and a formal aspect, and that some version of the modal/formal account is therefore closest to being correct.
-preservational" accounts, according to which the characteristic feature of a good inference is that it never allows one to move from justifiably assertible premises to a conclusion that is not justifiably assertible. This is (roughly) the account favored by intuitionists such as Michael Dummett
.
but not of
For more on this, see belief revision#Non-monotonic inference relation.
It is impossible to state rigorously the definition of 'logical implication' as it is understood pretheoretically, but many have taken the Tarskian model-theoretic account as a replacement for it. Some, e.g. , have argued that they do not coincide, not even if they happen to be co-extensional (which Etchemendy believes they are not). This debate has received some recent attention. See "The Blackwell Guide to Philosophical Logic", for a good introduction to it.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, entailment is a relation between a set of sentences (e.g., meaningfully declarative sentences or truthbearer
Truthbearer
Truth-bearer is a term used to designate entities that are either true or false and nothing else. The thesis that some things are true while others are false raises the question of the nature of these things. Since there is divergence of opinion on the matter, the term truthbearer is used to be...
s) and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent. S2 is called the logical consequent of Γ; S1 is said to logically imply S2.
Two sentences are inconsistent if and only if they cannot both be true; they are logically inconsistent if and only if they are inconsistent as a result of their logical form
Logical form
In logic, the logical form of a sentence or set of sentences is the form obtained by abstracting from the subject matter of its content terms or by regarding the content terms as mere placeholders or blanks on a form...
.
Thus if
- Γ = {“Roses are red”, “Violets are blue”},
- S1 = “Roses are red and Violets are blue”
and
- S2 = “Violets are Blue”
then Γ entails S2, because
- “Roses are red and Violets are blue”
and
- “Violets are not blue”
are logically inconsistent. They are logically inconsistent because as a result of their logical form they cannot be both true, their logical forms being p and q and not-q.
On the other hand if
- Γ = {“John is a bachelor”},
- S1 = “John is a bachelor” and
- S2 = “John is a man”
then Γ does not entail S2 because
- S1, “John is a bachelor”
andS2, “John is not a man”
are not logically inconsistent because they can both be true as a result of their logical form, their logical form being p and not-q.
Logical form
Given Γ is a set of one or more declarative sentences.Since
- Γ entails S2 if and only if S1 and not-S2 are logically inconsistent
and
- S1 and not-S2 are logically inconsistent if they are inconsistent as a result of their logical forms
it follows that
- Γ entails S2 if and only if S1 and not-S2 are inconsistent as a result of their logical forms.
It is therefore of the first importance to clarify the term logical form and explain how the logically relevant form(s) of a sentence can be established.
The logical form of sentences can be revealed by means of a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
enabling the following definition of entailment. Roughly, if S1 and S2 are interpretations of two sentences θ and ψ in a formal language of classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, then S1 entails S2 if and only if not (θ and not ψ) is true under all interpretations
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
.
More precisely, if Γ is a set of one or more sentences and S1 is the conjunction of the elements of Γ and S2 is a sentence, Γ entails S2 if and only if not (S1 and not-S2) is a logical truth
Logical truth
Logical truth is one of the most fundamental concepts in logic, and there are different theories on its nature. A logical truth is a statement which is true and remains true under all reinterpretations of its components other than its logical constants. It is a type of analytic statement.Logical...
. S2 is called the 'logical consequent' of Γ. S1 is said to 'logically imply' S2.
Not (S1 and not-S2) is a logical truth if θ and Ψ are closed well-formed formula
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
e (often denoted 'wff'), wffs (sentences) in a formal language L in classical logic, and I is an interpretation
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
of L, and θ is true under I if and only if S1 and Ψ is true under I if and only if S2, and not (θ and not Ψ) is logically valid
Validity
In logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
.
A closed wff Φ in L is 'logically valid' if and only if Φ is true under all interpretations of L. Hence
- Γ entails S2 iff not (θ and not Ψ) is logically validValidityIn logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
.
Thus if Γ = {“Roses are red”, “Violets are blue”}, S1=“Roses are red and Violets are blue” and S2 = “Violets are Blue” then Γ entails S2 because not(S1 and not-S2), “It is not the case that roses are red and violets are blue and violets are not blue” is a logical truth.
Not(S1 and not-S2) is a logical truth because there are two closed wfs, P&Q and Q in a formal language L in classical logic and there is an interpretation I of L, and P&Q is true under I if and only if roses are red and violets are blue, and Q is true under I if and only if violets are blue, and ¬((P&Q)&¬Q) is logically valid. ¬((P&Q)&¬Q)) is logically valid because it is true under all interpretations of L (note that ¬ means not
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
).
It will be noted that, on these definitions, if (i) S1 is inconsistent (self-contradictory) or (ii) not-S2 is inconsistent (self-contradictory) then (S1 and not-S2) is inconsistent (not consistent) and hence S1 entails S2.
Proof procedures, and Relationship between entailment and deduction
It is of considerable interest to be able to prove that Γ entails S2 and hence that Γ / S2 is a valid argument.Ideally, entailment and deduction
Deductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
would be extension
Extension (semantics)
In any of several studies that treat the use of signs - for example, in linguistics, logic, mathematics, semantics, and semiotics - the extension of a concept, idea, or sign consists of the things to which it applies, in contrast with its comprehension or intension, which consists very roughly of...
ally equivalent. However, this is not always the case. In such a case, it is useful to break the equivalence down into its two parts:
A deductive system
Deductive system
A deductive system consists of the axioms and rules of inference that can be used to derive the theorems of the system....
S is complete for a language L if and only if
implies 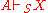: that is, if all validValid
Valid is a Brazilian engraving company headquartered in Rio de Janeiro that provides security printing services to financial institutions, telecommunication companies, state governments, and public agencies in Brazil, Argentina, and Spain....
arguments are deducible (or provable), where
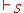denotes the deducibility relation for the system S. NB means that X is provable from A for a language L, and 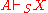means that X is a semantic consequence of A for the system S.A deductive system S is sound
Soundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
for a language L if and only if
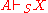implies : that is, if no invalid arguments are provable.Many introductory textbooks (e.g. Mendelson's "Introduction to Mathematical Logic") that introduce first-order logic, include a complete and sound inference system for the first-order logic. In contrast, second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
— which allows quantification over predicates — does not have a complete and sound inference system with respect to a full Henkin
Leon Henkin
Leon Albert Henkin was a logician at the University of California, Berkeley. He was principally known for the "Henkin's completeness proof": his version of the proof of the semantic completeness of standard systems of first-order logic.-The completeness proof:Henkin's result was not novel; it had...
(or standard) semantics.
Proof of Entailment
Since- Γ entails S2 iff not (θ and not Ψ) is logically validValidityIn logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
a proof that not (θ and not Ψ) is logically valid
Validity
In logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
would be a proof that Γ entails S2.
It can be easily demonstrated, for example by means of a truth-table, that ¬((P&Q)&¬Q) is a tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
and hence true under all interpretations and hence logically valid. Moreover, if T is a consistent theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
in L and ¬(θ∧¬Ψ) is a theorem in T (written ⊢T¬(θ∧¬Ψ)) then ¬(θ∧¬Ψ) is logically valid and, consequently, all interpretations of ¬(θ∧¬Ψ) are logical truths, including not(S1 and not-S2). Hence Γ entails S2 if ⊢T¬(θ∧¬Ψ) and T is consistent.
Relationship to other terms
Entailment is one of a number of inter-related terms of logical appraisal. Its relationship to other such terms includes the following see e.g. Strawson (1952) Section 13, 'Entailment and Inconsistency', pp 19 et seq) where S1 and S2 are sentences, or S1 is the conjunction of all the sentences in some set of sentences Γ,S1 entails S2 if and only if:
- S1 and not-S2 are inconsistent (not consistent)
- (S1 and not-S2) is logically impossible
- Not(S1 and not-S2) is logically trueLogical truthLogical truth is one of the most fundamental concepts in logic, and there are different theories on its nature. A logical truth is a statement which is true and remains true under all reinterpretations of its components other than its logical constants. It is a type of analytic statement.Logical...
- Not(S1 and not-S2) is necessarily true
- (S1 and not-S2) is logically false
- S1 is a sufficient condition for S2
- S2 is a necessary condition for S1
- It would be self-contradictory to affirm S1 and deny S2
- An argument whose premise is S1 and conclusion is S2 is a validValidityIn logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
argument - If S1 and S2 are interpretations of two sentences θ and ψ in a formal language of classical logic (elementary logic), then S1 entails S2 if and only if not (θ and ¬ψ) is true in all interpretationsInterpretation (logic)An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
.
Syntactic consequence
A formula A is a syntactic consequence within some formal systemFormal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
FS of a set Г of formulas if there is a formal proof
Formal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
in FS of A from the set Г.
Syntactic consequence does not depend on any interpretation
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
of the formal system.
Semantic consequence
A formula A is a semantic consequence of a set of statements Г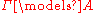,if and only if no interpretation
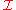makes all members of Г true and A false. Or, in other words, the set of the interpretations that make all members of Г true is a subset of the set of the interpretations that make A true.Entailment vs material implication
The difference between material implication and entailment is that they apply in different contexts. The first is a statement of logic, the second of metalogic. If p and q are two sentences then the difference between "p implies q" and "p is a proof of q" is that the first is a statement within formal logic, the second is a statement about it. Entailment is a concept of proof theory, whereas material implication is the mechanics of a proof.Limitations
Entailment is one form but not the only form of inferenceInference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
. Inductive reasoning
Inductive reasoning
Inductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
is another. Scientific method
Scientific method
Scientific method refers to a body of techniques for investigating phenomena, acquiring new knowledge, or correcting and integrating previous knowledge. To be termed scientific, a method of inquiry must be based on gathering empirical and measurable evidence subject to specific principles of...
involves inferences that are not solely entailment. Entailment does not encompass non-monotonic reasoning or defeasible reasoning
Defeasible reasoning
Defeasible reasoning is a kind of reasoning that is based on reasons that are defeasible, as opposed to the indefeasible reasons of deductive logic...
. See also
- Reasoning
- Abductive reasoningAbductive reasoningAbduction is a kind of logical inference described by Charles Sanders Peirce as "guessing". The term refers to the process of arriving at an explanatory hypothesis. Peirce said that to abduce a hypothetical explanation a from an observed surprising circumstance b is to surmise that a may be true...
- Deductive reasoningDeductive reasoningDeductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
- Inductive reasoningInductive reasoningInductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
- Open world assumptionOpen World AssumptionIn formal logic, the open world assumption is the assumption that the truth-value of a statement is independent of whether or not it is known by any single observer or agent to be true. It is the opposite of the closed world assumption, which holds that any statement that is not known to be true is...
Modal accounts
Modal accounts of logical consequence are variations on the following basic idea:- Γ
A just in case it is necessary that if all of the elements of Γ are true, then A is true.
Alternatively (and, most would say, equivalently):
- Γ
A just in case it is impossible for all of the elements of Γ to be true and A false.
Such accounts are called "modal" because they appeal to the modal notions of necessity and (im)possibility
Logical possibility
A logically possible proposition is one that can be asserted without implying a logical contradiction. This is to say that a proposition is logically possible if there is some coherent way for the world to be, under which the proposition would be true...
. 'It is necessary that' is often cashed out as a universal quantifier over possible worlds
Possible Worlds
Possible Worlds may refer to:* Possible worlds, a concept in philosophy* Possible Worlds , by John Mighton** Possible Worlds , by Robert Lepage, based on the Mighton play* Possible Worlds , by Peter Porter...
, so that the accounts above translate as:
- Γ
A just in case there is no possible world at which all of the elements of Γ are true and A is false (untrue).
Consider the modal account in terms of the argument given as an example above:
- All frogs are green.
- Kermit is a frog.
- Therefore, Kermit is green.
The conclusion is a logical consequence of the premises because we can't imagine a possible world where (a) all frogs are green; (b) Kermit is a frog; and (c) Kermit is not green.
Modal-formal accounts
Modal-formal accounts of logical consequence combine the modal and formal accounts above, yielding variations on the following basic idea:- Γ
A just in case it is impossible for an argument with the same logical form as Γ/A to have true premises and a false conclusion.
Most logicians would probably agree that logical consequence, as we intuitively understand it, has both a modal and a formal aspect, and that some version of the modal/formal account is therefore closest to being correct.
Warrant-based accounts
The accounts considered above are all "truth-preservational," in that they all assume that the characteristic feature of a good inference is that it never allows one to move from true premises to an untrue conclusion. As an alternative, some have proposed "warrantTheory of justification
Theory of justification is a part of epistemology that attempts to understand the justification of propositions and beliefs. Epistemologists are concerned with various epistemic features of belief, which include the ideas of justification, warrant, rationality, and probability...
-preservational" accounts, according to which the characteristic feature of a good inference is that it never allows one to move from justifiably assertible premises to a conclusion that is not justifiably assertible. This is (roughly) the account favored by intuitionists such as Michael Dummett
Michael Dummett
Sir Michael Anthony Eardley Dummett FBA D.Litt is a British philosopher. He was, until 1992, Wykeham Professor of Logic at the University of Oxford...
.
Non-monotonic logical consequence
The accounts discussed above all yield monotonic consequence relations, i.e. ones such that if A is a consequence of Γ, then A is a consequence of any superset of Γ. It is also possible to specify non-monotonic consequence relations to capture the idea that, e.g., 'Tweety can fly' is a logical consequence of- {Birds can typically fly, Tweety is a bird}
but not of
- {Birds can typically fly, Tweety is a bird, Tweety is a penguin}.
For more on this, see belief revision#Non-monotonic inference relation.
Philosophical issues
- The literature is ambiguous regarding precisely what 'logical implication' means. Sometimes it is taken to be a pretheoretic notion capable of definition in several ways, usually involving modality and stated something like "A set of sentences logically implies a sentence A if and only if it is impossible that all the members of the set be true while A false". Other times it is taken as the definition given in the introduction to this article, perhaps as a replacement for the pretheoretic notion itself. This often occurs in the sciences and mathematics; that is, intuitive notions get replaced by more precise, rigorously defined ones. E.g., in mathematics, many now take 'computable' in the sense of 'effectively calculable' to be 'computable' in the sense of TuringAlan TuringAlan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
, ChurchAlonzo ChurchAlonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
, GodelKurt GödelKurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
, HerbrandJacques HerbrandJacques Herbrand was a French mathematician who was born in Paris, France and died in La Bérarde, Isère, France. Although he died at only 23 years of age, he was already considered one of "the greatest mathematicians of the younger generation" by his professors Helmut Hasse, and Richard Courant.He...
, or PostEmil Leon PostEmil Leon Post was a mathematician and logician. He is best known for his work in the field that eventually became known as computability theory.-Early work:...
.
It is impossible to state rigorously the definition of 'logical implication' as it is understood pretheoretically, but many have taken the Tarskian model-theoretic account as a replacement for it. Some, e.g. , have argued that they do not coincide, not even if they happen to be co-extensional (which Etchemendy believes they are not). This debate has received some recent attention. See "The Blackwell Guide to Philosophical Logic", for a good introduction to it.
- It is often thought that a peculiar feature of logical implication is that a contradiction implies anything and that anything implies a validity. For example, 'Abraham Lincoln was president of the US' implies '2+2=4', and 'the white dot is black' implies 'the integer 25 is greater than the integer 30'. The peculiarity in these examples is oft-attributed to a lack of relevance between the two sentences. A formal notion of relevance has been characterized by relevant logic and applied to the notion of logical implication in the seminal work of . Another property they argue that implication should have is necessity. Thus A implies B only if it is necessary that A implies B. This feature of implication is lacking in the usual model-theoretic definition (i.e. the one given in the introduction).
- Some logicians draw a firm distinction between the conditional connective (the syntactic sign "
"), and the implication relation (the formal object denoted by the double arrow symbol "
"). These logicians use the phrase not p or q for the conditional connective and the term implies for the implication relation. Some explain the difference by saying that the conditional is the contemplated relation while the implication is the asserted relation. In most fields of mathematics, it is treated as a variation in the usage of the single sign "
", not requiring two separate signs. Not all of those who use the sign "
" for the conditional connective regard it as a sign that denotes any kind of object, but treat it as a so-called syncategorematic sign, that is, a sign with a purely syntactic function. For the sake of clarity and simplicity in the present introduction, it is convenient to use the two-sign notation, but allow the sign "
" to denote the boolean function that is associated with the truth tableTruth tableA truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
of the material conditional. These considerations result in the following scheme of notation.
-
See also
- Abstract algebraic logicAbstract Algebraic LogicIn mathematical logic, abstract algebraic logic is the study of the algebraization of deductive systemsarising as an abstraction of the well-known Lindenbaum-Tarski algebra, and how the resulting algebras are related to logical systems.-Overview:...
- Ampheck
- Boolean algebra (logic)
- Boolean domainBoolean domainIn mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true...
- Boolean function
- Boolean logicBoolean logicBoolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
- Deductive reasoningDeductive reasoningDeductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
- Logic gateLogic gateA logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and...
- Logical graphLogical graphA logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
- Peirce's lawPeirce's lawIn logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely...
- Propositional calculusPropositional calculusIn mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
- Sole sufficient operator
- Tautology (logic)Tautology (logic)In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
- Therefore signTherefore signIn a mathematical proof, the therefore sign is a symbol that is sometimes placed before a logical consequence, such as the conclusion of a syllogism. The symbol consists of three dots placed in an upright triangle and is read therefore. It is encoded at . While it is not generally used in formal...
- Turnstile (symbol)Turnstile (symbol)In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
- Double turnstileDouble turnstileIn logic, the symbol \vDash is called the double turnstile. It is closely related to the turnstile symbol, which has a single bar across the middle. It is often read as "models" or "is a semantic consequence of". In TeX, the turnstile symbol \vDash is obtained from the command \vDash...
- ValidityValidityIn logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
Resources
1st edition, Kluwer Academic Publishers, Norwell, MA. 2nd edition, Dover Publications, Mineola, NY, 2003.. Papers include those by GödelGodelGodel or similar can mean:*Kurt Gödel , an Austrian logician, mathematician and philosopher*Gödel...
, ChurchAlonzo ChurchAlonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
, Rosser, Kleene, and Post.. in Lou Goble (ed.), The Blackwell Guide to Philosophical Logic. in Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy... 365-409. in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
(1st ed. 1950), (2nd ed. 1959), (3rd ed. 1972), (4th edition, 1982). in D. Jacquette, ed., A Companion to Philosophical Logic. Blackwell. Reprinted in Tarski, A., 1983. Logic, Semantics, Metamathematics, 2nd ed. Oxford University PressOxford University PressOxford University Press is the largest university press in the world. It is a department of the University of Oxford and is governed by a group of 15 academics appointed by the Vice-Chancellor known as the Delegates of the Press. They are headed by the Secretary to the Delegates, who serves as...
. Originally published in PolishPolish languagePolish is a language of the Lechitic subgroup of West Slavic languages, used throughout Poland and by Polish minorities in other countries...
and GermanGerman languageGerman is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
.
- A paper on 'implication' from math.niu.edu, Implication
- A definition of 'implicant' AllWords
External links
- Abstract algebraic logic