Linking number - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the linking number is a numerical invariant

Invariant (mathematics)

In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...

that describes the linking of two closed curves in three-dimensional space

Three-dimensional space

Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...

. Intuitively, the linking number represents the number of times that each curve winds around the other. The linking number is always an integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

, but may be positive or negative depending on the orientation

Curve orientation

In mathematics, a positively oriented curve is a planar simple closed curve such that when traveling on it one always has the curve interior to the left...

of the two curves.

The linking number was introduced by Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

in the form of the linking integral. It is an important object of study in knot theory

Knot theory

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

, algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

, and differential geometry, and has numerous applications in mathematics

Mathematics

and science

Science

Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...

, including quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

, electromagnetism

Electromagnetism

Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...

, and the study of DNA supercoil

DNA supercoil

DNA supercoiling refers to the over- or under-winding of a DNA strand, and is an expression of the strain on the polymer. Supercoiling is important in a number of biological processes, such as compacting DNA. Additionally, certain enzymes such as topoisomerases are able to change DNA topology to...

ing.

Definition

Any two closed curves in space can be moved

Homotopy

In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...

into exactly one of the following standard positions. This determines the linking number:


linking number -2	linking number -1	linking number 0

	linking number 1	linking number 2	linking number 3

Each curve may pass through itself during this motion, but the two curves must remain separated throughout. This is formalized as regular homotopy

Regular homotopy

In the mathematical field of topology, a regular homotopy refers to a special kind of homotopy between immersions of one manifold in another. The homotopy must be a 1-parameter family of immersions....

, which further requires that each curve be an immersion, not just any map. However, this added condition does not change the definition of linking number (it does not matter if the curves are required to always be immersions or not), which is an example of an h-principle

H-principle

In mathematics, the homotopy principle is a very general way to solve partial differential equations , and more generally partial differential relations...

(homotopy-principle), meaning that geometry reduces to topology.

Proof

This fact (that the linking number is the only invariant) is most easily proven by placing one circle in standard position, and then show that linking number is the only invariant of the other circle. In detail:

A single curve is regular homotopic to a standard circle (any knot can be unknotted if the curve is allowed to pass through itself). The fact that it is homotopic is clear, since 3-space is contractible and thus all maps into it are homotopic, though the fact that this can be done through immersions requires some geometric argument.
The complement of a standard circle is homeomorphic to a solid torus with a point removed (this can be seen by interpreting 3-space as the 3-sphere with the point at infinity removed, and the 3-torus as two solid tori glued along the boundary), or the complement can be analyzed directly.
The fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

of 3-space minus a circle is the integers, corresponding to linking number. This can be seen via the Seifert–Van Kampen theorem
Seifert–van Kampen theorem
In mathematics, the Seifert-van Kampen theorem of algebraic topology, sometimes just called van Kampen's theorem, expresses the structure of the fundamental group of a topological space X, in terms of the fundamental groups of two open, path-connected subspaces U and V that cover X...

(either adding the point at infinity to get a solid torus, or adding the circle to get 3-space, allows one to computer the fundamental group of the desired space).
Thus homotopy classes of a curve in 3-space minus a circle are determined by linking number.
It is also true that regular homotopy classes are determined by linking number, which requires additional geometric argument.

Computing the linking number

There is an algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

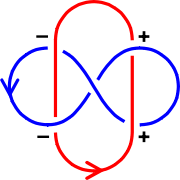
to compute the linking number of two curves from a link diagram. Label each crossing as positive or negative, according to the following rule:

The total number of positive crossings minus the total number of negative crossings is equal to twice the linking number. That is:

where n₁, n₂, n₃, n₄ represent the number of crossings of each of the four types. The two sums

and

are always equal, which leads to the following alternative formula

Note that

involves only the undercrossings of the blue curve by the red, while

involves only the overcrossings.

Properties and examples

Any two unlinked curves have linking number zero. However, two curves with linking number zero may still be linked (e.g. the Whitehead link
Whitehead link
In knot theory, the Whitehead link, discovered by J.H.C. Whitehead, is one of the most basic links.J.H.C. Whitehead spent much of the 1930s looking for a proof of the Poincaré conjecture...

).
Reversing the orientation of either of the curves negates the linking number, while reversing the orientation of both curves leaves it unchanged.
The linking number is chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...

: taking the mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...

of link negates the linking number. Our convention for positive linking number is based on a right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....

.
The winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...

of an oriented curve in the x-y plane is equal to its linking number with the z-axis (thinking of the z-axis as a closed curve in the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...

).
More generally, if either of the curves is simple, then the first homology group
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...

of its complement is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...

to Z
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

. In this case, the linking number is determined by the homology class of the other curve.
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, the linking number is an example of a topological quantum number
Topological quantum number
In physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...

. It is related to quantum entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...

.

Gauss's integral definition

Given two non-intersecting differentiable curves

, define the Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

map

from the torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

to the sphere

Unit sphere

In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...

Pick a point in the unit sphere, v, so that orthogonal projection of the link to the plane perpendicular to v gives a link diagram. Observe that a point (s,t) that goes to v under the Gauss map corresponds to a crossing in the link diagram where

is over

. Also, a neighborhood of (s,t) is mapped under the Gauss map to a neighborhood of v preserving or reversing orientation depending on the sign of the crossing. Thus in order to compute the linking number of the diagram corresponding to v it suffices to count the signed number of times the Gauss map covers v. Since v is a regular value, this is precisely the degree

Degree of a continuous mapping

In topology, the degree is a numerical invariant that describes a continuous mapping between two compact oriented manifolds of the same dimension. Intuitively, the degree represents the number of times that the domain manifold wraps around the range manifold under the mapping...

of the Gauss map (i.e. the signed number of times that the image

Image (mathematics)

In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...

of Γ covers the sphere). Isotopy invariance of the linking number is automatically obtained as the degree is invariant under homotopic maps. Any other regular value would give the same number, so the linking number doesn't depend on any particular link diagram.

This formulation of the linking number of γ₁ and γ₂ enables an explicit formula as a double line integral

Line integral

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...

, the Gauss linking integral:

This integral computes the total signed area of the image of the Gauss map (the integrand being the Jacobian

Jacobian

In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...

of Γ) and then divides by the area of the sphere (which is 4π).

Generalizations