.gif)
Minor (graph theory)
Encyclopedia
In graph theory
, an undirected graph H is called a minor of the graph G if H is isomorphic
to a graph that can be obtained by zero or more edge contraction
s on a subgraph of G.
The theory of graph minors began with Wagner's theorem that a graph is planar
if and only if it does not contain the complete graph
K5 nor the complete bipartite graph
K3,3 as a minor. The Robertson-Seymour theorem states that the relation "being a minor of" is a well-quasi-ordering
on the isomorphism classes of graphs, and implies that many other families of graphs have forbidden minor characterizations similar to that for the planar graphs.
Graph minors are often studied in the more general context of matroid
minors. In this context, it is common to assume that all graphs are connected, with self-loops
and multiple edges allowed (that is, they are multigraph
s rather than simple graphs; the contraction of a loop and the deletion of a cut-edge are forbidden operations. This point of view has the advantage that edge deletions leave the rank
of a graph unchanged, and edge contractions always reduce the rank by one.
In other contexts (such as with the study of pseudoforest
s) it makes more sense to allow the deletion of a cut-edge, and to allow disconnected graphs, but to forbid multigraphs. In this variation of graph minor theory, a graph is always simplified after any edge contraction to eliminate its self-loops and multiple edges.
H.
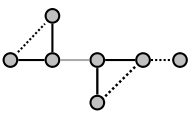
G.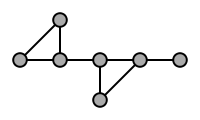 
The following diagram illustrates this. First construct a subgraph of G by deleting the dashed edges (and the resulting isolated vertex), and then contract the gray edge (merging the two vertices it connects):
forms a partial order on the isomorphism classes of undirected graphs: it satisfies the transitive property
(a minor of a minor of G is a minor of G itself), and G and H can only be minors of each other if they are isomorphic because any nontrivial minor operation removes edges. A deep result by Neil Robertson
and Paul Seymour states that this partial order is actually a well-quasi-ordering
: if an infinite list G1, G2,... of finite graphs is given, then there always exist two indices i < j such that Gi is a minor of Gj. Another equivalent way of stating this is that any set of graphs can have only a finite number of minimal elements under the minor ordering. This result proved a conjecture formerly known as Wagner's conjecture, after Klaus Wagner
; Wagner had conjectured it long earlier, but only published it in 1970.
In the course of their proof, Seymour and Robertson also prove the graph structure theorem
in which they determine, for any fixed graph H, the rough structure of any graph which does not have H as a minor. The statement of the theorem is itself long and involved, but in short it establishes that such a graph must have the structure of a clique-sum
of smaller graphs that are modified in small ways from graphs embedded
on surfaces of bounded genus
.
Thus, their theory establishes fundamental connections between graph minors and topological embeddings
of graphs.
For any graph H, the simple H-minor-free graphs must be sparse, which means that the number of edges is less than some constant multiple of the number of vertices. More specifically, if H has h vertices, then a simple n-vertex simple H-minor-free graph can have at most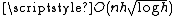
edges, and some Kh-minor-free graphs have at least this many edges. Additionally, the H-minor-free graphs have a separator theorem similar to the planar separator theorem
for planar graphs: for any fixed H, and any n-vertex H-minor-free graph G, it is possible to find a subset of O(√n) vertices the removal of which splits G into two (possibly disconnected) subgraphs with at most 2n/3 vertices per subgraph.
The Hadwiger conjecture
in graph theory proposes that if a graph G does not contain a minor isomorphic to the complete graph
on k vertices, then G has a proper coloring
with k − 1 colors. The case k = 5 is a restatement of the four color theorem
. The Hadwiger conjecture has been proven only for k ≤ 6, but remains unproven in the general case. call it “one of the deepest unsolved problems in graph theory.” Another result relating the four-color theorem to graph minors is the snark theorem announced by Robertson, Sanders, Seymour, and Thomas, a strengthening of the four-color theorem conjectured by W. T. Tutte
and stating that any bridgeless
3-regular graph
that requires four colors in an edge coloring
must have the Petersen graph
as a minor.
Many families of graphs have the property that every minor of a graph in F is also in F; such a class is said to be minor-closed. For instance, in any planar graph
, or any embedding
of a graph on a fixed topological surface, neither the removal of edges nor the contraction of edges can increase the genus
of the embedding; therefore, planar graphs and the graphs embeddable on any fixed surface form minor-closed families.
If F is a minor-closed family, then (because of the well-quasi-ordering property of minors) among the graphs that do not belong to F there is a finite set X of minor-minimal graphs. These graphs are forbidden minors for F: a graph belongs to F if and only if it does not contain as a minor any graph in X. That is, every minor-closed family F can be characterized as the family of X-minor-free graphs for some finite set X of forbidden minors.
The best-known example of a characterization of this type is Wagner's theorem characterizing the planar graphs as the graphs having neither K5 nor K3,3 as minors.
In some cases, the properties of the graphs in a minor-closed family may be closely connected to the properties of their excluded minors. For example a minor-closed graph family F has bounded pathwidth if and only if its forbidden minors include a forest
, F has bounded cycle rank
if and only if its forbidden minors include a disjoint union of path graph
s, F has bounded treewidth if and only if its forbidden minors include a planar graph
, and F has bounded local treewidth (a functional relationship between diameter and treewidth) if and only if its forbidden minors include an apex graph
(a graph that can be made planar by the removal of a single vertex). If H can be drawn in the plane with only a single crossing (that is, it has crossing number
one) then the H-minor-free graphs have a simplified structure theorem in which they are formed as clique-sums of planar graphs and graphs of bounded treewidth. For instance, both K5 and K3,3 have crossing number one, and as Wagner showed the K5-free graphs are exactly the 3-clique-sums of planar graphs and the eight-vertex Wagner graph
, while the K3,3-free graphs are exactly the 2-clique-sums of planar graphs and K5.
See "Robertson-Seymour theorem" for a list of minor-closed graph families.
A graph H is called a topological minor of a graph G if a subdivision of H is isomorphic
to a subgraph of G. It is easy to see that every topological minor is also a minor. The converse however is not true in general, but holds for graph with maximum degree not greater than 3.
The topological minor relation is not a well-quasi-ordering on the set of finite graphs and hence the result of Robertson and Seymour does not apply to topological minors. However it is straightforward to construct finite forbidden topological minor characterizations from finite forbidden minor characterizations by replacing every branch set with k outgoing edges by every tree on k leaves that has down degree at least two.
whether a graph G contains H as a minor is NP-complete in general; for instance, if H is a cycle graph
with the same number of vertices as G, then H is a minor of G if and only if G contains a Hamiltonian cycle. However, when G is part of the input but H is fixed, it can be solved in polynomial time. More specifically, the running time for testing whether H is a minor of G in this case is O(n3), where n is the number of vertices in G and the big O notation
hides a constant that depends superexponentially on H. Thus, by applying the polynomial time algorithm for testing whether a given graph contains any of the forbidden minors, it is possible to recognize the members of any minor-closed family in polynomial time. However, in order to apply this result constructively, it is necessary to know what the forbidden minors of the graph family are.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an undirected graph H is called a minor of the graph G if H is isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
to a graph that can be obtained by zero or more edge contraction
Edge contraction
In graph theory, an edge contraction is an operation which removes an edge from a graph while simultaneously merging together the two vertices it previously connected. Edge contraction is a fundamental operation in the theory of graph minors...
s on a subgraph of G.
The theory of graph minors began with Wagner's theorem that a graph is planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
if and only if it does not contain the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K5 nor the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K3,3 as a minor. The Robertson-Seymour theorem states that the relation "being a minor of" is a well-quasi-ordering
Well-quasi-ordering
In mathematics, specifically order theory, a well-quasi-ordering or wqo is a well-founded quasi-ordering with an additional restriction on sequences - that there is no infinite sequence x_i with x_i \not \le x_j for all i...
on the isomorphism classes of graphs, and implies that many other families of graphs have forbidden minor characterizations similar to that for the planar graphs.
Definitions
An edge contraction is an operation which removes an edge from a graph while simultaneously merging together the two vertices it used to connect. An undirected graph H is a minor of another undirected graph G if a graph isomorphic to H can be obtained from G by contracting some edges, deleting some edges, and deleting some isolated vertices. The order in which a sequence of such contractions and deletions is performed on G does not affect the resulting graph H.Graph minors are often studied in the more general context of matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
minors. In this context, it is common to assume that all graphs are connected, with self-loops
Loop (graph theory)
In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
and multiple edges allowed (that is, they are multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
s rather than simple graphs; the contraction of a loop and the deletion of a cut-edge are forbidden operations. This point of view has the advantage that edge deletions leave the rank
Rank (graph theory)
In graph theory, a branch of mathematics, the rank of an undirected graph is defined as the number , where is the number of vertices and is the number of connected components of the graph...
of a graph unchanged, and edge contractions always reduce the rank by one.
In other contexts (such as with the study of pseudoforest
Pseudoforest
In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be...
s) it makes more sense to allow the deletion of a cut-edge, and to allow disconnected graphs, but to forbid multigraphs. In this variation of graph minor theory, a graph is always simplified after any edge contraction to eliminate its self-loops and multiple edges.
Example
In the following example, graph H is a minor of graph G:H.
Major results and conjectures
It is straightforward to verify that the Graph minor relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
forms a partial order on the isomorphism classes of undirected graphs: it satisfies the transitive property
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
(a minor of a minor of G is a minor of G itself), and G and H can only be minors of each other if they are isomorphic because any nontrivial minor operation removes edges. A deep result by Neil Robertson
Neil Robertson (mathematician)
G. Neil Robertson is a mathematician working mainly in topological graph theory, currently a distinguished professor at the Ohio State University. He earned his Ph.D. in 1969 at the University of Waterloo under his doctoral advisor William Tutte. According to the criteria of the Erdős Number...
and Paul Seymour states that this partial order is actually a well-quasi-ordering
Well-quasi-ordering
In mathematics, specifically order theory, a well-quasi-ordering or wqo is a well-founded quasi-ordering with an additional restriction on sequences - that there is no infinite sequence x_i with x_i \not \le x_j for all i...
: if an infinite list G1, G2,... of finite graphs is given, then there always exist two indices i < j such that Gi is a minor of Gj. Another equivalent way of stating this is that any set of graphs can have only a finite number of minimal elements under the minor ordering. This result proved a conjecture formerly known as Wagner's conjecture, after Klaus Wagner
Klaus Wagner (mathematician)
Klaus Wagner was a German mathematician. He studied topology at the University of Cologne under the supervision of Karl Dörge, who had been a student of Issai Schur. Wagner received his Ph.D. in 1937, and taught at Cologne for many years himself...
; Wagner had conjectured it long earlier, but only published it in 1970.
In the course of their proof, Seymour and Robertson also prove the graph structure theorem
Graph structure theorem
In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and...
in which they determine, for any fixed graph H, the rough structure of any graph which does not have H as a minor. The statement of the theorem is itself long and involved, but in short it establishes that such a graph must have the structure of a clique-sum
Clique-sum
In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology...
of smaller graphs that are modified in small ways from graphs embedded
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
on surfaces of bounded genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
.
Thus, their theory establishes fundamental connections between graph minors and topological embeddings
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
of graphs.
For any graph H, the simple H-minor-free graphs must be sparse, which means that the number of edges is less than some constant multiple of the number of vertices. More specifically, if H has h vertices, then a simple n-vertex simple H-minor-free graph can have at most
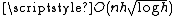edges, and some Kh-minor-free graphs have at least this many edges. Additionally, the H-minor-free graphs have a separator theorem similar to the planar separator theoremPlanar separator theorem
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices...
for planar graphs: for any fixed H, and any n-vertex H-minor-free graph G, it is possible to find a subset of O(√n) vertices the removal of which splits G into two (possibly disconnected) subgraphs with at most 2n/3 vertices per subgraph.
The Hadwiger conjecture
Hadwiger conjecture (graph theory)
In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...
in graph theory proposes that if a graph G does not contain a minor isomorphic to the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on k vertices, then G has a proper coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
with k − 1 colors. The case k = 5 is a restatement of the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
. The Hadwiger conjecture has been proven only for k ≤ 6, but remains unproven in the general case. call it “one of the deepest unsolved problems in graph theory.” Another result relating the four-color theorem to graph minors is the snark theorem announced by Robertson, Sanders, Seymour, and Thomas, a strengthening of the four-color theorem conjectured by W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
and stating that any bridgeless
Bridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
3-regular graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
that requires four colors in an edge coloring
Edge coloring
In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
must have the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
as a minor.
Minor-closed graph families
Many families of graphs have the property that every minor of a graph in F is also in F; such a class is said to be minor-closed. For instance, in any planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, or any embedding
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
of a graph on a fixed topological surface, neither the removal of edges nor the contraction of edges can increase the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
of the embedding; therefore, planar graphs and the graphs embeddable on any fixed surface form minor-closed families.
If F is a minor-closed family, then (because of the well-quasi-ordering property of minors) among the graphs that do not belong to F there is a finite set X of minor-minimal graphs. These graphs are forbidden minors for F: a graph belongs to F if and only if it does not contain as a minor any graph in X. That is, every minor-closed family F can be characterized as the family of X-minor-free graphs for some finite set X of forbidden minors.
The best-known example of a characterization of this type is Wagner's theorem characterizing the planar graphs as the graphs having neither K5 nor K3,3 as minors.
In some cases, the properties of the graphs in a minor-closed family may be closely connected to the properties of their excluded minors. For example a minor-closed graph family F has bounded pathwidth if and only if its forbidden minors include a forest
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, F has bounded cycle rank
Cycle rank
In graph theory, the cycle rank of a directed graph is a digraph connectivity measure proposed first by Eggan and Büchi . Intuitively, this concept measures how close adigraph is to a directed acyclic graph , in the sense that a DAG has...
if and only if its forbidden minors include a disjoint union of path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
s, F has bounded treewidth if and only if its forbidden minors include a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, and F has bounded local treewidth (a functional relationship between diameter and treewidth) if and only if its forbidden minors include an apex graph
Apex graph
In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex...
(a graph that can be made planar by the removal of a single vertex). If H can be drawn in the plane with only a single crossing (that is, it has crossing number
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
one) then the H-minor-free graphs have a simplified structure theorem in which they are formed as clique-sums of planar graphs and graphs of bounded treewidth. For instance, both K5 and K3,3 have crossing number one, and as Wagner showed the K5-free graphs are exactly the 3-clique-sums of planar graphs and the eight-vertex Wagner graph
Wagner graph
In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.-Properties:...
, while the K3,3-free graphs are exactly the 2-clique-sums of planar graphs and K5.
See "Robertson-Seymour theorem" for a list of minor-closed graph families.
Topological minors
A graph H is called a topological minor of a graph G if a subdivision of H is isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
to a subgraph of G. It is easy to see that every topological minor is also a minor. The converse however is not true in general, but holds for graph with maximum degree not greater than 3.
The topological minor relation is not a well-quasi-ordering on the set of finite graphs and hence the result of Robertson and Seymour does not apply to topological minors. However it is straightforward to construct finite forbidden topological minor characterizations from finite forbidden minor characterizations by replacing every branch set with k outgoing edges by every tree on k leaves that has down degree at least two.
Algorithms
The problem of decidingDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
whether a graph G contains H as a minor is NP-complete in general; for instance, if H is a cycle graph
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
with the same number of vertices as G, then H is a minor of G if and only if G contains a Hamiltonian cycle. However, when G is part of the input but H is fixed, it can be solved in polynomial time. More specifically, the running time for testing whether H is a minor of G in this case is O(n3), where n is the number of vertices in G and the big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
hides a constant that depends superexponentially on H. Thus, by applying the polynomial time algorithm for testing whether a given graph contains any of the forbidden minors, it is possible to recognize the members of any minor-closed family in polynomial time. However, in order to apply this result constructively, it is necessary to know what the forbidden minors of the graph family are.