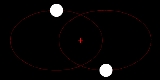
Gravitational two-body problem
Encyclopedia
For further relevant mathematical developments see also Two-body problem
, also Kepler orbit
, and Kepler problem
, and Equation of the center – Analytical expansions
The gravitational two-body problem
concerns the motion of two point particles that interact only with each other, due to gravity. This means that influences from any third body are neglected. For approximate results that is often suitable. It also means that the two bodies stay clear of each other, that is, the two do not collide
, and one body does not pass through the other's atmosphere
. Even if they do, the theory still holds for the part of the orbit where they don't. Apart from these considerations a spherically symmetric body can be approximated by a point mass.
Common examples include the parts of a spaceflight
where the spacecraft is not undergoing propulsion and atmospheric effects are negligible, and a single celestial body overwhelmingly dominates the gravitational influence. Other common examples are the orbit of a moon
around a planet
, and of a planet around a star
, and two stars orbiting each other (a binary star
).
The reduced mass
multiplied by the relative acceleration between the two bodies is equal to the gravitational force. The latter is proportional to the product of the two masses, which is equal to the reduced mass multiplied by the sum of the masses. Thus in the differential equation the two occurrences of the reduced mass cancel each other, and we get the same differential equation as for the position of a very small body orbiting a body with a mass equal to the sum of the two masses.
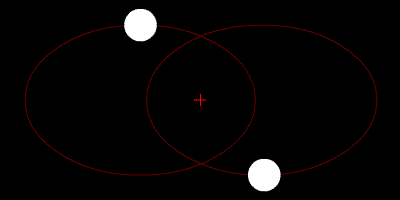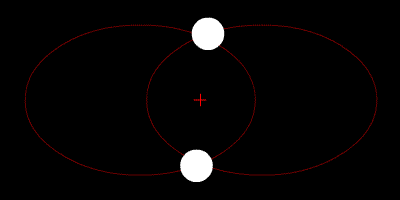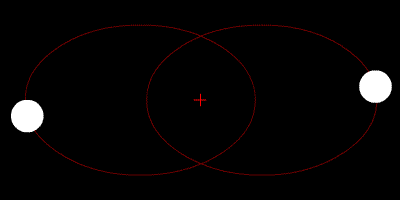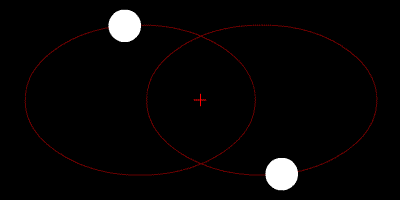
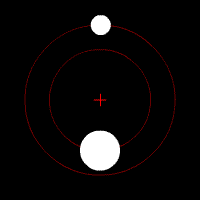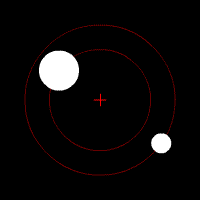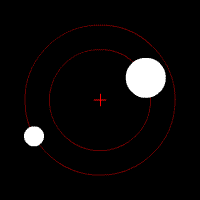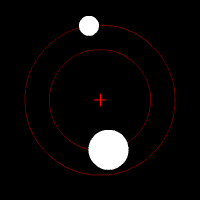
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
, also Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
, and Kepler problem
Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
, and Equation of the center – Analytical expansions
The gravitational two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
concerns the motion of two point particles that interact only with each other, due to gravity. This means that influences from any third body are neglected. For approximate results that is often suitable. It also means that the two bodies stay clear of each other, that is, the two do not collide
Collision
A collision is an isolated event which two or more moving bodies exert forces on each other for a relatively short time.Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies...
, and one body does not pass through the other's atmosphere
Atmosphere
An atmosphere is a layer of gases that may surround a material body of sufficient mass, and that is held in place by the gravity of the body. An atmosphere may be retained for a longer duration, if the gravity is high and the atmosphere's temperature is low...
. Even if they do, the theory still holds for the part of the orbit where they don't. Apart from these considerations a spherically symmetric body can be approximated by a point mass.
Common examples include the parts of a spaceflight
Spaceflight
Spaceflight is the act of travelling into or through outer space. Spaceflight can occur with spacecraft which may, or may not, have humans on board. Examples of human spaceflight include the Russian Soyuz program, the U.S. Space shuttle program, as well as the ongoing International Space Station...
where the spacecraft is not undergoing propulsion and atmospheric effects are negligible, and a single celestial body overwhelmingly dominates the gravitational influence. Other common examples are the orbit of a moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
around a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
, and of a planet around a star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
, and two stars orbiting each other (a binary star
Binary star
A binary star is a star system consisting of two stars orbiting around their common center of mass. The brighter star is called the primary and the other is its companion star, comes, or secondary...
).
The reduced mass
Reduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
multiplied by the relative acceleration between the two bodies is equal to the gravitational force. The latter is proportional to the product of the two masses, which is equal to the reduced mass multiplied by the sum of the masses. Thus in the differential equation the two occurrences of the reduced mass cancel each other, and we get the same differential equation as for the position of a very small body orbiting a body with a mass equal to the sum of the two masses.


- Assume:
-
- the vector r is the position of one body relative to the other
- r, v, the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
a, and the specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
h are defined accordingly (hence r is the distance) - h is the total angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
divided by the reduced mass 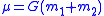 , the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
, the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
(the sum of those for each mass)
-
- where:
-
 and
and 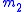 are the masses of the two bodies.
are the masses of the two bodies.
-
- Then:
-
- the general solution is (see also the orbit equationOrbit equationIn astrodynamics an orbit equation defines the path of orbiting body m_2\,\! around central body m_1\,\! relative to m_1\,\!, without specifying position as a function of time...
and two-body problem for an inverse-square force):
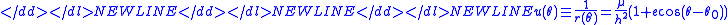
-
-
- for any non-negative e, called the eccentricityOrbital eccentricityThe orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
- the positions of the bodies with respect to the barycenterBarycentric coordinates (astronomy)In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
are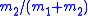 and
and 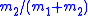 times r, respectively, so the two bodies' orbits are similarSimilarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
times r, respectively, so the two bodies' orbits are similarSimilarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s; the same ratios apply for the velocities, and, without the minus, for the angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
and for the kinetic energies, all with respect to the barycenter - for circular orbitCircular orbitA circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
s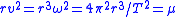
- for elliptic orbitElliptic orbitIn astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
s: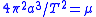 (with a expressed in AU and T in years, and with M the total mass relative to that of the Sun, we get
(with a expressed in AU and T in years, and with M the total mass relative to that of the Sun, we get 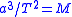 )
) - for parabolic trajectoriesParabolic trajectoryIn astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1. When moving away from the source it is called an escape orbit, otherwise a capture orbit...
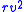 is constant and equal to
is constant and equal to 
- the formulas for the specific orbital energySpecific orbital energyIn the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
 apply, with specific potential and kinetic energy and their sum taken as the totals for the system, divided by the reduced mass; the kinetic energy of the smaller body is larger; the potential energy of the whole system is equal to the potential energy of one body with respect to the other, i.e. minus the energy needed to escape the other if the other is kept in a fixed position; this should not be confused with the smaller amount of energy one body needs to escape, if the other body moves away also, in the opposite direction: in that case the total energy the two need to escape each other is the same as the aforementioned amount; the conservation of energy for each mass means that an increase of kinetic energy is accompanied by a decrease of potential energy, which is for each mass the inner product of the force and the change in position relative to the barycenter, not relative to the other mass
apply, with specific potential and kinetic energy and their sum taken as the totals for the system, divided by the reduced mass; the kinetic energy of the smaller body is larger; the potential energy of the whole system is equal to the potential energy of one body with respect to the other, i.e. minus the energy needed to escape the other if the other is kept in a fixed position; this should not be confused with the smaller amount of energy one body needs to escape, if the other body moves away also, in the opposite direction: in that case the total energy the two need to escape each other is the same as the aforementioned amount; the conservation of energy for each mass means that an increase of kinetic energy is accompanied by a decrease of potential energy, which is for each mass the inner product of the force and the change in position relative to the barycenter, not relative to the other mass - for elliptic and hyperbolic orbits
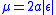
- for any non-negative e, called the eccentricity
-
- For example, consider two bodies like the Sun orbiting each other:
-
- the reduced mass is one half of the mass of one Sun (one quarter of the total mass)
- at a distance of 1 AU: the orbital periodOrbital periodThe orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
is year, the same as the orbital period of the Earth would be if the Sun had twice its actual mass; the total energy per kg reduced mass (90 MJ/kg) is twice that of the Earth-Sun system (45 MJ/kg); the total energy per kg total mass (22.5 MJ/kg) is one half of the total energy per kg Earth mass in the Earth-Sun system (45 MJ/kg)
year, the same as the orbital period of the Earth would be if the Sun had twice its actual mass; the total energy per kg reduced mass (90 MJ/kg) is twice that of the Earth-Sun system (45 MJ/kg); the total energy per kg total mass (22.5 MJ/kg) is one half of the total energy per kg Earth mass in the Earth-Sun system (45 MJ/kg) - at a distance of 2 AU (each following an orbit like that of the Earth around the Sun): the orbital period is 2 years, the same as the orbital period of the Earth would be if the Sun would have one quarter of its actual mass
- at a distance of
 AU: the orbital period is 1 year, the same as the orbital period of the Earth around the Sun
AU: the orbital period is 1 year, the same as the orbital period of the Earth around the Sun
-
-
- Similarly, a second Earth at a distance from the Earth equal to
 times the usual distance of geosynchronous orbitGeosynchronous orbitA geosynchronous orbit is an orbit around the Earth with an orbital period that matches the Earth's sidereal rotation period...
times the usual distance of geosynchronous orbitGeosynchronous orbitA geosynchronous orbit is an orbit around the Earth with an orbital period that matches the Earth's sidereal rotation period...
s would be geosynchronous.
- Similarly, a second Earth at a distance from the Earth equal to
Examples
Any classical system of two particles is, by definition, a two-body problem. In many cases, however, one particle is significantly heavier than the other, e.g., the EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
and the SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
. In such cases, the heavier particle is approximately the center of mass, and the reduced mass is approximately the lighter mass. Hence, the heavier mass may be treated roughly as a fixed center of force, and the motion of the lighter mass may be solved for directly by one-body methods.
In other cases, however, the masses of the two bodies are roughly equal, so that neither of them can be approximated as being at rest. Astronomical examples include:
- a binary starBinary starA binary star is a star system consisting of two stars orbiting around their common center of mass. The brighter star is called the primary and the other is its companion star, comes, or secondary...
, e.g. Alpha CentauriAlpha CentauriAlpha Centauri is the brightest star in the southern constellation of Centaurus...
(approx. the same mass) - a double planetDouble planetIn astronomy, double planet and binary planet are informal terms used to describe a binary system of two astronomical objects that each satisfy the definition of planet and that are near enough to each other to have a significant gravitational effect on each other compared with the effect of the...
, e.g. PlutoPlutoPluto, formal designation 134340 Pluto, is the second-most-massive known dwarf planet in the Solar System and the tenth-most-massive body observed directly orbiting the Sun...
with its moon CharonCharon (moon)Charon is the largest satellite of the dwarf planet Pluto. It was discovered in 1978 at the United States Naval Observatory Flagstaff Station. Following the 2005 discovery of two other natural satellites of Pluto , Charon may also be referred to as Pluto I...
(mass ratio 0.147) - a binary asteroidBinary asteroidA binary asteroid is a system of two asteroids orbiting their common center of mass, in analogy with binary stars. 243 Ida was the first binary asteroid to be identified when the Galileo spacecraft did a flyby in 1993...
, e.g. 90 Antiope90 AntiopeThe most remarkable feature of Antiope is that it consists of two components of almost equal size , making it a truly "double" asteroid. Its binary nature was discovered on 10 August 2000 by a group of astronomers using adaptive optics at the Keck Telescope on Mauna Kea. The "secondary" is...
(approx. the same mass)
See also
- Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
- Kepler's laws of planetary motionKepler's laws of planetary motionIn astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
- Virial theorem
- n-body problemN-body problemThe n-body problem is the problem of predicting the motion of a group of celestial objects that interact with each other gravitationally. Solving this problem has been motivated by the need to understand the motion of the Sun, planets and the visible stars...
- Bertrand's theorem
- Kepler problemKepler problemIn classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
-
- the general solution is (see also the orbit equation
-

