
Kepler problem
Encyclopedia
In classical mechanics
, the Kepler problem is a special case of the two-body problem
, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive. The "problem" to be solved is to find the position or speed of the two bodies over time given their masses and initial positions and velocities. Using classical mechanics, the solution can be expressed as a Kepler orbit
using six orbital elements
.
The Kepler problem is named after Johannes Kepler
, who proposed Kepler's laws of planetary motion
(which are part of classical mechanics
and solve the problem for the orbits of the planets) and investigated the types of forces that would result in orbits obeying those laws (called Kepler's inverse problem).
For a discussion of the Kepler problem specific to radial orbits, see: Radial trajectory
. The Kepler problem in general relativity
produces more accurate predictions, especially in strong gravitational fields.
, since Newtonian gravity
obeys an inverse square law. Examples include a satellite moving about a planet, a planet about its sun, or two binary stars about each other. The Kepler problem is also important in the motion of two charged particles, since Coulomb’s law of electrostatics
also obeys an inverse square law. Examples include the hydrogen
atom, positronium
and muonium
, which have all played important roles as model systems for testing physical theories and measuring constants of nature.
The Kepler problem and the simple harmonic oscillator problem are the two most fundamental problems in classical mechanics
. They are the only two problems that have closed orbits for every possible set of initial conditions, i.e., return to their starting point with the same velocity (Bertrand's theorem). The Kepler problem has often been used to develop new methods in classical mechanics, such as Lagrangian mechanics
, Hamiltonian mechanics
, the Hamilton–Jacobi equation
, and action-angle coordinates
. The Kepler problem also conserves the Laplace–Runge–Lenz vector, which has since been generalized to include other interactions. The solution of the Kepler problem allowed scientists to show that planetary motion could be explained entirely by classical mechanics and Newton’s law of gravity
; the scientific explanation of planetary motion played an important role in ushering in the Enlightenment
.
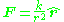
where k is a constant and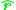 represents the unit vector along the line between them. The force may be either attractive (k<0) or repulsive (k>0). The corresponding scalar potential
represents the unit vector along the line between them. The force may be either attractive (k<0) or repulsive (k>0). The corresponding scalar potential
(the potential energy
of the non-central body) is:
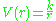
 of a particle
of a particle
of mass moving in a central potential
moving in a central potential 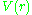 is given by Lagrange's equations
is given by Lagrange's equations
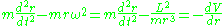
where and the angular momentum
and the angular momentum
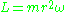 is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force
is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force 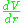 equals the centripetal force requirement
equals the centripetal force requirement
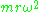 , as expected.
, as expected.
If L is not zero the definition of angular momentum
allows a change of independent variable from to
to 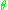

giving the new equation of motion that is independent of time
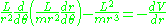
This equation becomes quasilinear on making the change of variables and multiplying both sides by
and multiplying both sides by 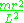
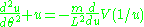
For an inverse-square force law such as the gravitational or electrostatic potential
, the potential
can be written
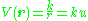
The orbit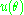 can be derived from the general equation
can be derived from the general equation
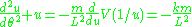
whose solution is the constant plus a simple sinusoid
plus a simple sinusoid
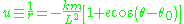
where (the eccentricity) and
(the eccentricity) and 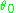 (the phase offset) are constants of integration.
(the phase offset) are constants of integration.
This is the general formula for a conic section
that has one focus at the origin;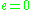 corresponds to a circle
corresponds to a circle
,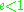 corresponds to an ellipse,
corresponds to an ellipse, 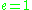 corresponds to a parabola
corresponds to a parabola
, and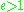 corresponds to a hyperbola
corresponds to a hyperbola
. The eccentricity is related to the total energy
is related to the total energy
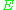 (cf. the Laplace–Runge–Lenz vector)
(cf. the Laplace–Runge–Lenz vector)
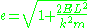
Comparing these formulae shows that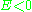 corresponds to an ellipse (all solutions which are closed orbits
corresponds to an ellipse (all solutions which are closed orbits
are ellipses), corresponds to a parabola
corresponds to a parabola
, and corresponds to a hyperbola
corresponds to a hyperbola
. In particular, for perfectly circular
for perfectly circular
orbits (the central force exactly equals the centripetal force requirement
, which determines the required angular velocity for a given circular radius).
For a repulsive force (k > 0) only e > 1 applies.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the Kepler problem is a special case of the two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive. The "problem" to be solved is to find the position or speed of the two bodies over time given their masses and initial positions and velocities. Using classical mechanics, the solution can be expressed as a Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
using six orbital elements
Orbital elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are generally considered in classical two-body systems, where a Kepler orbit is used...
.
The Kepler problem is named after Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, who proposed Kepler's laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
(which are part of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and solve the problem for the orbits of the planets) and investigated the types of forces that would result in orbits obeying those laws (called Kepler's inverse problem).
For a discussion of the Kepler problem specific to radial orbits, see: Radial trajectory
Radial trajectory
In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.- Classification :...
. The Kepler problem in general relativity
Kepler problem in general relativity
The two-body problem in general relativity is to determine the motion and gravitational field of two bodies interacting with one another by gravitation, as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of light by gravity...
produces more accurate predictions, especially in strong gravitational fields.
Applications
The Kepler problem arises in many contexts, some beyond the physics studied by Kepler himself. The Kepler problem is important in celestial mechanicsCelestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, since Newtonian gravity
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
obeys an inverse square law. Examples include a satellite moving about a planet, a planet about its sun, or two binary stars about each other. The Kepler problem is also important in the motion of two charged particles, since Coulomb’s law of electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
also obeys an inverse square law. Examples include the hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
atom, positronium
Positronium
Positronium is a system consisting of an electron and its anti-particle, a positron, bound together into an "exotic atom". Being unstable, the two particles annihilate each other to produce two gamma ray photons after an average lifetime of 125 ps or three gamma ray photons after 142 ns in...
and muonium
Muonium
Muonium is an exotic atom made up of an antimuon and an electron, which was discovered in 1960 and is given the chemical symbol . During the muon's lifetime, muonium can enter into compounds such as muonium chloride or sodium muonide . Due to the mass difference between the antimuon and the...
, which have all played important roles as model systems for testing physical theories and measuring constants of nature.
The Kepler problem and the simple harmonic oscillator problem are the two most fundamental problems in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. They are the only two problems that have closed orbits for every possible set of initial conditions, i.e., return to their starting point with the same velocity (Bertrand's theorem). The Kepler problem has often been used to develop new methods in classical mechanics, such as Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, the Hamilton–Jacobi equation
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
, and action-angle coordinates
Action-angle coordinates
In classical mechanics, action-angle coordinates are a set of canonical coordinates useful in solving many integrable systems. The method of action-angles is useful for obtaining the frequencies of oscillatory or rotational motion without solving the equations of motion. Action-angle coordinates...
. The Kepler problem also conserves the Laplace–Runge–Lenz vector, which has since been generalized to include other interactions. The solution of the Kepler problem allowed scientists to show that planetary motion could be explained entirely by classical mechanics and Newton’s law of gravity
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
; the scientific explanation of planetary motion played an important role in ushering in the Enlightenment
Age of Enlightenment
The Age of Enlightenment was an elite cultural movement of intellectuals in 18th century Europe that sought to mobilize the power of reason in order to reform society and advance knowledge. It promoted intellectual interchange and opposed intolerance and abuses in church and state...
.
Mathematical definition
The central force F that varies in strength as the inverse square of the distance r between them: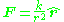
where k is a constant and
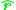 represents the unit vector along the line between them. The force may be either attractive (k<0) or repulsive (k>0). The corresponding scalar potential
represents the unit vector along the line between them. The force may be either attractive (k<0) or repulsive (k>0). The corresponding scalar potentialScalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
(the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of the non-central body) is:
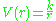
Solution of the Kepler problem
The equation of motion for the radius of a particle
of a particleof mass
 moving in a central potential
moving in a central potential 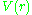 is given by Lagrange's equations
is given by Lagrange's equations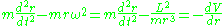
where
 and the angular momentum
and the angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
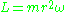 is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force
is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force 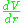 equals the centripetal force requirement
equals the centripetal force requirementCentripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
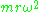 , as expected.
, as expected.If L is not zero the definition of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
allows a change of independent variable from
 to
to 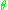

giving the new equation of motion that is independent of time
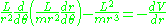
This equation becomes quasilinear on making the change of variables
 and multiplying both sides by
and multiplying both sides by 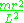
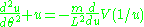
For an inverse-square force law such as the gravitational or electrostatic potential
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, the potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
can be written
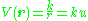
The orbit
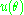 can be derived from the general equation
can be derived from the general equation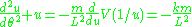
whose solution is the constant
 plus a simple sinusoid
plus a simple sinusoid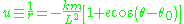
where
 (the eccentricity) and
(the eccentricity) and 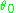 (the phase offset) are constants of integration.
(the phase offset) are constants of integration.This is the general formula for a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
that has one focus at the origin;
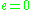 corresponds to a circle
corresponds to a circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
,
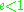 corresponds to an ellipse,
corresponds to an ellipse, 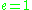 corresponds to a parabola
corresponds to a parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and
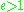 corresponds to a hyperbola
corresponds to a hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. The eccentricity
 is related to the total energy
is related to the total energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
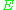 (cf. the Laplace–Runge–Lenz vector)
(cf. the Laplace–Runge–Lenz vector)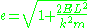
Comparing these formulae shows that
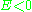 corresponds to an ellipse (all solutions which are closed orbits
corresponds to an ellipse (all solutions which are closed orbitsOrbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
are ellipses),
 corresponds to a parabola
corresponds to a parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and
 corresponds to a hyperbola
corresponds to a hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. In particular,
 for perfectly circular
for perfectly circularCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
orbits (the central force exactly equals the centripetal force requirement
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
, which determines the required angular velocity for a given circular radius).
For a repulsive force (k > 0) only e > 1 applies.
See also
- Action-angle coordinatesAction-angle coordinatesIn classical mechanics, action-angle coordinates are a set of canonical coordinates useful in solving many integrable systems. The method of action-angles is useful for obtaining the frequencies of oscillatory or rotational motion without solving the equations of motion. Action-angle coordinates...
- Bertrand's theorem
- Binet equationBinet equationThe Binet equation, derived by Jacques Philippe Marie Binet, provides the form of a central force given the shape of the orbital motion in plane polar coordinates. The equation can also be used to derive the shape of the orbit for a given force law, but this usually involves the solution to a...
- Hamilton–Jacobi equationHamilton–Jacobi equationIn mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
- Laplace–Runge–Lenz vector
- Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
- Kepler problem in general relativityKepler problem in general relativityThe two-body problem in general relativity is to determine the motion and gravitational field of two bodies interacting with one another by gravitation, as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of light by gravity...
- Kepler's equationKepler's equationKepler's equation is M = E -\epsilon \cdot \sin E ,where M is the mean anomaly, E is the eccentric anomaly, and \displaystyle \epsilon is the eccentricity....
- Kepler's laws of planetary motionKepler's laws of planetary motionIn astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....

