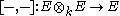Graded Lie algebra
Encyclopedia
In mathematics
, a graded Lie algebra is a Lie algebra
endowed with a gradation
which is compatible with the Lie bracket
. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition
endows any semisimple Lie algebra with the structure of a graded Lie algebra. Any parabolic Lie algebra
is also a graded Lie algebra.
A graded Lie superalgebra extends the notion of a graded Lie algebra in such a way that the Lie bracket is no longer assumed to be necessarily anticommutative. These arise in the study of derivation
s on graded algebra
s, in the deformation theory
of M. Gerstenhaber
, Kunihiko Kodaira, and D. C. Spencer, and in the theory of Lie derivative
s.
A supergraded Lie superalgebra is a further generalization of this notion to the category of superalgebra
s in which a graded Lie superalgebra is endowed with an additional super Z/2Z-gradation. These arise when one forms a graded Lie superalgebra in a classical (non-supersymmetric) setting, and then tensorizes to obtain the supersymmetric
analog.
Still greater generalizations are possible to Lie algebras over a class of braided monoidal categories equipped with a coproduct
and some notion of a gradation compatible with the braiding in the category. For hints in this direction, see Lie algebra#Category theory definition.
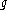, together with a gradation of vector spaces:
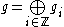(1)
such that the Lie bracket respects this gradation: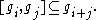
(2)
The universal enveloping algebra
of a graded Lie algebra inherits the grading.
is graded by the generators: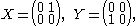
and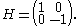
These satisfy the relations [X,Y] = H, [H,X] = 2X, [H,Y] = -2Y. Hence with
g-1 = span(X), g0 = span(H), and g1 = span(Y),
the decomposition sl(2) = g-1 + g0 + g1 presents sl(2) as a graded Lie algebra.
on a set X naturally has a grading, given by the minimum number of terms needed to generate the group element. This arises for example as the associated graded Lie algebra to the lower central series of a free group
.
E over k, along with a bilinear
bracket operation
such that the following axioms are satisfied.
Note, for instance, that when E carries the trivial gradation, a graded Lie superalgebra over k is just an ordinary Lie algebra. When the gradation of E is concentrated in even degrees, one recovers the definition of a (Z-) graded Lie algebra.
with gradation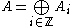
,
then a graded k-derivation d on A of degree l is defined by
The space of all graded derivations of degree l is denoted by Derl(A), and the direct sum of these spaces
carries the structure of an A-module. This generalizes the notion of a derivation of commutative algebras to the graded category.
On Der(A), one can define a bracket via:
Equipped with this structure, Der(A) inherits the structure of a graded Lie superalgebra over k.
Further examples:
and ε : Γ → Z/2Z is a homomorphism
of additive groups. Then a graded Lie supalgebra over a signed semiring consists of a vector space E graded with respect to the additive structure on Γ, and a bilinear bracket [-,-] which respects the grading on E and in addition satisfies:
Further examples:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a graded Lie algebra is a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
endowed with a gradation
Graded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
which is compatible with the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition
Cartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
endows any semisimple Lie algebra with the structure of a graded Lie algebra. Any parabolic Lie algebra
Parabolic Lie algebra
In algebra, a parabolic Lie algebra \mathfrak p is a subalgebra of a semisimple Lie algebra \mathfrak g satisfying one of the following two conditions:* \mathfrak p contains a maximal solvable subalgebra of \mathfrak g;...
is also a graded Lie algebra.
A graded Lie superalgebra extends the notion of a graded Lie algebra in such a way that the Lie bracket is no longer assumed to be necessarily anticommutative. These arise in the study of derivation
Derivation
Derivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
s on graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
s, in the deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of M. Gerstenhaber
Murray Gerstenhaber
Murray Gerstenhaber is an American mathematician, professor of mathematics at the University of Pennsylvania, best known for his contributions to theoretical physics with his discovery of Gerstenhaber algebra.- About :...
, Kunihiko Kodaira, and D. C. Spencer, and in the theory of Lie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
s.
A supergraded Lie superalgebra is a further generalization of this notion to the category of superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
s in which a graded Lie superalgebra is endowed with an additional super Z/2Z-gradation. These arise when one forms a graded Lie superalgebra in a classical (non-supersymmetric) setting, and then tensorizes to obtain the supersymmetric
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
analog.
Still greater generalizations are possible to Lie algebras over a class of braided monoidal categories equipped with a coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
and some notion of a gradation compatible with the braiding in the category. For hints in this direction, see Lie algebra#Category theory definition.
Graded Lie algebras
In its most basic form, a graded Lie algebra is an ordinary Lie algebra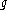, together with a gradation of vector spaces: 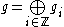(1)such that the Lie bracket respects this gradation:
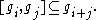(2)The universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of a graded Lie algebra inherits the grading.
sl(2)
For example, the Lie algebra sl(2) of trace-free 2x2 matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is graded by the generators:
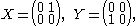and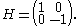These satisfy the relations [X,Y] = H, [H,X] = 2X, [H,Y] = -2Y. Hence with
g-1 = span(X), g0 = span(H), and g1 = span(Y),
the decomposition sl(2) = g-1 + g0 + g1 presents sl(2) as a graded Lie algebra.
Free Lie algebra
The free Lie algebraFree Lie algebra
In mathematics, a free Lie algebra, over a given field K, is a Lie algebra generated by a set X, without any imposed relations.-Definition:Given a set X, one can show that there exists a unique free Lie algebra L generated by X....
on a set X naturally has a grading, given by the minimum number of terms needed to generate the group element. This arises for example as the associated graded Lie algebra to the lower central series of a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
.
Generalizations
If Γ is any commutative monoid, then the notion of a Γ-graded Lie algebra generalizes that of an ordinary (Z-) graded Lie algebra so that the defining relations (1) and (2) hold with the integers Z replaced by Γ. In particular, any semisimple Lie algebra is graded by the root spaces of its adjoint representation.Graded Lie superalgebras
A graded Lie superalgebra over a field k (not of characteristic 2) consists of a graded vector spaceGraded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
E over k, along with a bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
bracket operation
such that the following axioms are satisfied.
- [-,-] respects the gradation of E:
-
.
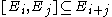- (Symmetry.) If x ε Ei and y ε Ej, then
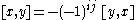
- (Jacobi identity.) If x ε Ei, y ε Ej, and z ε Ek, then
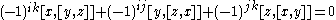.- (If k has characteristic 3, then the Jacobi identity must be supplemented with the condition
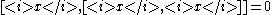for all x in Eodd.)
Note, for instance, that when E carries the trivial gradation, a graded Lie superalgebra over k is just an ordinary Lie algebra. When the gradation of E is concentrated in even degrees, one recovers the definition of a (Z-) graded Lie algebra.
Examples and Applications
The most basic example of a graded Lie superalgebra occurs in the study of derivations of graded algebras. If A is a graded k-algebraGraded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
with gradation
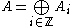,then a graded k-derivation d on A of degree l is defined by
- dx = 0 for x ε k,
- d : Ai → Ai+l, and
- d(xy) = (dx)y + (-1)ilx(dy) for x ε Ai.
The space of all graded derivations of degree l is denoted by Derl(A), and the direct sum of these spaces
carries the structure of an A-module. This generalizes the notion of a derivation of commutative algebras to the graded category.
On Der(A), one can define a bracket via:
- [d,δ]=d δ - (-1)ijδ d, for d ε Deri(A) and δ ε Derj(A).
Equipped with this structure, Der(A) inherits the structure of a graded Lie superalgebra over k.
Further examples:
- The Frölicher-Nijenhuis bracketFrölicher-Nijenhuis bracketIn mathematics, the Frölicher–Nijenhuis bracket is an extension of the Lie bracket of vector fields to vector-valued differential forms on a differentiable manifold...
is an example of a graded Lie algebra arising naturally in the study of connectionsConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
in differential geometry. - The Nijenhuis-Richardson bracket arises in connection with the deformations of Lie algebras.
Generalizations
The notion of a graded Lie superalgebra can be generalized so that their grading is not just the integers. Specifically, a signed semiring consists of a pair (Γ, ε) where Γ is a semiringSemiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
and ε : Γ → Z/2Z is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of additive groups. Then a graded Lie supalgebra over a signed semiring consists of a vector space E graded with respect to the additive structure on Γ, and a bilinear bracket [-,-] which respects the grading on E and in addition satisfies:
-
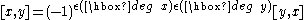for all homogeneous elements x and y, and -
Further examples:
- A Lie superalgebraLie superalgebraIn mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
is a graded Lie superalgebra over the signed semiring (Z/2Z,ε) where ε is the identity endomorphism for the additive structure on the ring Z/2Z.