
Friedmann equations
Encyclopedia

Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s in physical cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
that govern the expansion of space
Metric expansion of space
The metric expansion of space is the increase of distance between distant parts of the universe with time. It is an intrinsic expansion—that is, it is defined by the relative separation of parts of the universe and not by motion "outward" into preexisting space...
in homogeneous
Homogeneity (physics)
In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
and isotropic
Isotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
models of the universe within the context of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. They were first derived by Alexander Friedmann in 1922 from Einstein's field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
of gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
for the Friedmann-Lemaître-Robertson-Walker metric and a fluid with a given mass density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
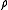 and pressure
and pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
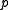 . The equations for negative spatial curvature were given by Friedmann in 1924.
. The equations for negative spatial curvature were given by Friedmann in 1924.Assumptions
The Friedmann equations start with the simplifying assumption that the universe is spatially homogeneous and isotropic, i.e. the Cosmological PrincipleCosmological Principle
In modern physical cosmology, the cosmological principle is the working assumption that observers on Earth do not occupy an unusual or privileged location within the universe as a whole, judged as observers of the physical phenomena produced by uniform and universal laws of physics...
; empirically, this is justified on scales larger than ~100 Mpc
Parsec
The parsec is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion kilometres ....
. The Cosmological Principle implies that the metric of the universe must be of the form:
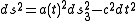
where
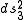 is a three dimensional metric that must be one of (a) flat space, (b) a sphere of constant positive curvature or (c) a hyperbolic space with constant negative curvature. The parameter
is a three dimensional metric that must be one of (a) flat space, (b) a sphere of constant positive curvature or (c) a hyperbolic space with constant negative curvature. The parameter 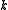 discussed below takes the value 0, 1, -1 in these three cases respectively. It is this fact that allows us to sensibly speak of a "scale factor
discussed below takes the value 0, 1, -1 in these three cases respectively. It is this fact that allows us to sensibly speak of a "scale factorScale factor (Universe)
The scale factor or cosmic scale factor parameter of the Friedmann equations is a function of time which represents the relative expansion of the universe. It is sometimes called the Robertson-Walker scale factor...
",
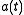 .
.Einstein's equations now relate the evolution of this scale factor to the pressure and energy of the matter in the universe. The resulting equations are described below.
The equations
There are two independent Friedmann equations for modeling a homogeneous, isotropic universe. They are: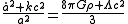
which is derived from the 00 component of Einstein's field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
, and
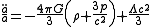
which is derived from the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of Einstein's field equations.
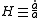 is the Hubble parameter, G, Λ, and c are universal constants (G is Newton's gravitational constant
is the Hubble parameter, G, Λ, and c are universal constants (G is Newton's gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, Λ is the cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
, c is the speed of light in vacuum
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
). k is constant throughout a particular solution, but may vary from one solution to another. a, H, ρ, and p are functions of time.
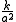 is the spatial curvature
is the spatial curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
in any time-slice of the universe; it is equal to one-sixth of the spatial Ricci curvature scalar R
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
since
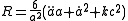 in the Friedmann model. There are two commonly used choices for a and k which describe the same physics:
in the Friedmann model. There are two commonly used choices for a and k which describe the same physics:
- k = +1, 0 or -1 depending on whether the shape of the universeShape of the UniverseThe shape of the universe is a matter of debate in physical cosmology over the local and global geometry of the universe which considers both curvature and topology, though, strictly speaking, it goes beyond both...
is a closed 3-sphere3-sphereIn mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
, flat (i.e. Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
) or an open 3-hyperboloid, respectively. If k = +1, then is the radius of curvature of the universe. If k = 0, then a may be fixed to any arbitrary positive number at one particular time. If k = -1, then (loosely speaking) one can say that i·a is the radius of curvature of the universe.
is the radius of curvature of the universe. If k = 0, then a may be fixed to any arbitrary positive number at one particular time. If k = -1, then (loosely speaking) one can say that i·a is the radius of curvature of the universe. - a is the scale factorScale factor (Universe)The scale factor or cosmic scale factor parameter of the Friedmann equations is a function of time which represents the relative expansion of the universe. It is sometimes called the Robertson-Walker scale factor...
which is taken to be 1 at the present time.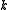 is the spatial curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
is the spatial curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
when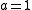 (i.e. today). If the shape of the universeShape of the UniverseThe shape of the universe is a matter of debate in physical cosmology over the local and global geometry of the universe which considers both curvature and topology, though, strictly speaking, it goes beyond both...
(i.e. today). If the shape of the universeShape of the UniverseThe shape of the universe is a matter of debate in physical cosmology over the local and global geometry of the universe which considers both curvature and topology, though, strictly speaking, it goes beyond both...
is hyperspherical and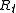 is the radius of curvature (
is the radius of curvature ( in the present-day), then
in the present-day), then  . If
. If 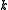 is positive, then the universe is hyperspherical. If
is positive, then the universe is hyperspherical. If 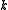 is zero, then the universe is flat. If
is zero, then the universe is flat. If  is negative, then the universe is hyperbolic.
is negative, then the universe is hyperbolic.
Using the first equation, the second equation can be re-expressed as
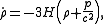
which eliminates
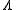 and expresses the conservation of mass-energy.
and expresses the conservation of mass-energy.These equations are sometimes simplified by replacing

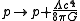
to give:
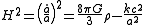
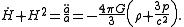
And the simplified form of the second equation is invariant under this transformation.
The Hubble parameter can change over time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
if other parts of the equation are time dependent (in particular the mass density, the vacuum energy, or the spatial curvature). Evaluating the Hubble parameter at the present time yields Hubble's constant which is the proportionality constant of Hubble's law
Hubble's law
Hubble's law is the name for the astronomical observation in physical cosmology that: all objects observed in deep space are found to have a doppler shift observable relative velocity to Earth, and to each other; and that this doppler-shift-measured velocity, of various galaxies receding from...
. Applied to a fluid with a given equation of state
Equation of state (cosmology)
In cosmology, the equation of state of a perfect fluid is characterized by a dimensionless number \! w, equal to the ratio of its pressure \! p to its energy density \! \rho: \! w=p/\rho...
, the Friedmann equations yield the time evolution and geometry of the universe as a function of the fluid density.
Some cosmologists call the second of these two equations the Friedmann acceleration equation and reserve the term Friedmann equation for only the first equation.
Density parameter
The density parameter,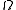 , is defined as the ratio of the actual (or observed) density
, is defined as the ratio of the actual (or observed) density  to the critical density
to the critical density 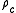 of the Friedmann universe. The relation between the actual density and the critical density determines the overall geometry of the universe.
of the Friedmann universe. The relation between the actual density and the critical density determines the overall geometry of the universe.In earlier models, which did not include a cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
term, critical density was regarded also as the watershed between an expanding and a contracting Universe.
To date, the critical density is estimated to be approximately five atoms (of monatomic hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
) per cubic metre, whereas the average density of ordinary matter in the Universe is believed to be 0.2 atoms per cubic metre. A much greater density comes from the unidentified dark matter
Dark matter
In astronomy and cosmology, dark matter is matter that neither emits nor scatters light or other electromagnetic radiation, and so cannot be directly detected via optical or radio astronomy...
; both ordinary and dark matter contribute in favor of contraction of the universe. However, the largest part comes from so-called dark energy
Dark energy
In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...
, which accounts for the cosmological constant term. Although the total density is equal to the critical density (exactly, up to measurement error), the dark energy does not lead to contraction of the universe but rather accelerates its expansion. Therefore, the universe will expand forever.
An expression for the critical density is found by assuming Λ to be zero (as it is for all basic Friedmann universes) and setting the normalised spatial curvature, k, equal to zero. When the substitutions are applied to the first of the Friedmann equations we find:
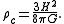
The density parameter (useful for comparing different cosmological models) is then defined as:
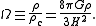
This term originally was used as a means to determine the spatial geometry
Shape of the Universe
The shape of the universe is a matter of debate in physical cosmology over the local and global geometry of the universe which considers both curvature and topology, though, strictly speaking, it goes beyond both...
of the universe, where
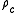 is the critical density for which the spatial geometry is flat (or Euclidean). Assuming a zero vacuum energy density, if
is the critical density for which the spatial geometry is flat (or Euclidean). Assuming a zero vacuum energy density, if 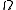 is larger than unity, the space sections of the universe are closed; the universe will eventually stop expanding, then collapse. If
is larger than unity, the space sections of the universe are closed; the universe will eventually stop expanding, then collapse. If  is less than unity, they are open; and the universe expands forever. However, one can also subsume the spatial curvature and vacuum energy terms into a more general expression for
is less than unity, they are open; and the universe expands forever. However, one can also subsume the spatial curvature and vacuum energy terms into a more general expression for 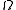 in which case this density parameter equals exactly unity. Then it is a matter of measuring the different components, usually designated by subscripts. According to the ΛCDM model
in which case this density parameter equals exactly unity. Then it is a matter of measuring the different components, usually designated by subscripts. According to the ΛCDM modelLambda-CDM model
ΛCDM or Lambda-CDM is an abbreviation for Lambda-Cold Dark Matter, which is also known as the cold dark matter model with dark energy...
, there are important components of
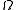 due to baryons, cold dark matter
due to baryons, cold dark matterCold dark matter
Cold dark matter is the improvement of the big bang theory that contains the additional assumption that most of the matter in the Universe consists of material that cannot be observed by its electromagnetic radiation and whose constituent particles move slowly...
and dark energy
Dark energy
In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...
. The spatial geometry of the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
has been measured by the WMAP spacecraft to be nearly flat. This means that the universe can be well approximated by a model where the spatial curvature parameter
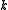 is zero; however, this does not necessarily imply that the universe is infinite: it might merely be that the universe is much larger than the part we see. (Similarly, the fact that Earth is approximately flat at the scale of a region does not imply that the Earth is flat: it only implies that it is much larger than this region.)
is zero; however, this does not necessarily imply that the universe is infinite: it might merely be that the universe is much larger than the part we see. (Similarly, the fact that Earth is approximately flat at the scale of a region does not imply that the Earth is flat: it only implies that it is much larger than this region.)The first Friedmann equation is often seen in a form with density parameters.

Here
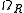 is the radiation density today (i.e. when
is the radiation density today (i.e. when  ),
),  is the matter (dark
is the matter (darkDark matter
In astronomy and cosmology, dark matter is matter that neither emits nor scatters light or other electromagnetic radiation, and so cannot be directly detected via optical or radio astronomy...
plus baryon
Baryon
A baryon is a composite particle made up of three quarks . Baryons and mesons belong to the hadron family, which are the quark-based particles...
ic) density today,
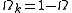 is the "spatial curvature density" today, and
is the "spatial curvature density" today, and 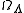 is the cosmological constant or vacuum density today.
is the cosmological constant or vacuum density today.Useful solutions
The Friedmann equations can be solved exactly in presence of a perfect fluidPerfect fluid
In physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
with equation of state
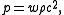
where
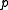 is the pressure
is the pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
,
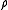 is the mass density of the fluid in the comoving frame and
is the mass density of the fluid in the comoving frame and 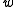 is some constant.
is some constant.In spatially flat case (k = 0), the solution for the scale factor is
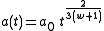
where
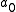 is some integration constant to be fixed by the choice of initial conditions. This family of solutions labelled by
is some integration constant to be fixed by the choice of initial conditions. This family of solutions labelled by 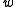 is extremely important for cosmology. E.g.
is extremely important for cosmology. E.g.  describes a matter-dominated
describes a matter-dominatedMatter-Dominated Era
The matter-dominated era was the epoch in the evolution of the Universe that began after the radiation-dominated era ended, when the Universe was about 70,000 years old. Although it was often said that we still live in the matter-dominated era, it is more correct to say that when the Universe was...
universe, where the pressure is negligible with respect to the mass density. From the generic solution one easily sees that in a matter-dominated universe the scale factor goes as
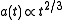 matter-dominated
matter-dominatedAnother important example is the case of a radiation-dominated
Radiation-Dominated Era
The radiation-dominated era refers to one of the three phases of the known universe, the other two being the matter-dominated era and the dark-energy-dominated era. During this era, the dynamics of the universe were set by radiation, which refers generally to the constituents of the universe which...
universe, i.e., when
 . This leads to
. This leads to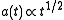 radiation dominated
radiation dominatedNote that this solution is not valid for domination of the cosmological constant, which corresponds to an
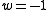 . In this case the energy density is constant and the scale factor grows exponentially.
. In this case the energy density is constant and the scale factor grows exponentially.Solutions for other values of k can be found at .
Mixtures
If the matter is a mixture of two or more non-interacting fluids each with such an equation of state, then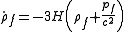
holds separately for each such fluid f. In each case,
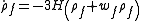
from which we get

For example, one can form a linear combination of such terms

where: A is the density of "dust" (ordinary matter, w=0) when a=1; B is the density of radiation (w=1/3) when a=1; and C is the density of "dark energy" (w=−1). One then substitutes this into
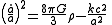
and solves for a as a function of time.
Rescaled Friedmann equation
Set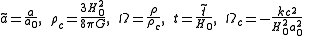 , where
, where 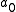 and
and 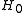 are separately the scale factor
are separately the scale factorScale factor (Universe)
The scale factor or cosmic scale factor parameter of the Friedmann equations is a function of time which represents the relative expansion of the universe. It is sometimes called the Robertson-Walker scale factor...
and the Hubble parameter today.
Then we can have
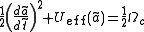
where
 . For any form of the effective potential
. For any form of the effective potential 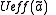 , there is an equation of state
, there is an equation of state 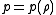 that will produce it.
that will produce it.See also
- UniverseUniverseThe Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
- Mathematics of general relativityMathematics of general relativityThe mathematics of general relativity refers to various mathematical structures and techniques that are used in studying and formulating Albert Einstein's theory of general relativity. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold...
- Solutions of Einstein's field equationsSolutions of the Einstein field equationsWhere appropriate, this article will use the abstract index notation.Solutions of the Einstein field equations are spacetimes that result from solving the Einstein field equations of general relativity. Solving the field equations actually gives Lorentz metrics...

