.gif)
E6 (mathematics)
Encyclopedia
In mathematics
, E6 is the name of some closely related Lie group
s, linear algebraic group
s or their Lie algebra
s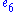
, all of which have dimension 78; the same notation E6 is used for the corresponding root lattice, which has rank 6. The designation E6 comes from the Cartan–Killing classification of the complex simple Lie algebras, which fall into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled E6, E7, E8
, F4, and G2. The E6 algebra is thus one of the five exceptional cases.
The fundamental group of the complex form, compact real form, or any algebraic version of E6 is the cyclic group
Z/3Z, and its outer automorphism group
is the cyclic group Z/2Z. Its fundamental representation
is 27-dimensional (complex), and a basis is given by the 27 lines on a cubic surface. The dual representation
, which is inequivalent, is also 27-dimensional.
In particle physics
, E6 plays a role in some grand unified theories.
78 can be considered as a simple real Lie group of real dimension 156. This has fundamental group Z/3Z, has maximal compact
subgroup the compact form (see below) of E6, and has an outer automorphism group non-cyclic of order 4 generated by complex conjugation and by the outer automorphism which already exists as a complex automorphism.
As well as the complex Lie group of type E6, there are five real forms of the Lie algebra, and correspondingly five real forms of the group with trivial center (all of which have an algebraic double cover, and three of which have further non-algebraic covers, giving further real forms), all of real dimension 78, as follows:
A certain noncompact real form of E6 is the group of collineations (line-preserving transformations) of the octonionic projective plane OP2. It is also the group of determinant-preserving linear transformations of the exceptional Jordan algebra
. The exceptional Jordan algebra is 27-dimensional, which explains why the compact real form of E6 has a 27-dimensional complex representation. The compact real form of E6 is the isometry group
of a 32-dimensional Riemannian manifold
known as the 'bioctonionic projective plane'.
for the Lie algebra, one can define E6 as a linear algebraic group over the integers and, consequently, over any commutative ring and in particular over any field: this defines the so-called split (sometimes also known as “untwisted”) adjoint form of E6. Over an algebraically closed field, this and its triple cover are the only forms; however, over other fields, there are often many other forms, or “twists” of E6, which are classified in the general framework of Galois cohomology
(over a perfect field
k) by the set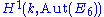
which, because the Dynkin diagram of E6 (see below) has automorphism group Z/2Z, maps to 
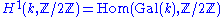with kernel 
.
Over the field of real numbers, the real component of the identity of these algebraically twisted forms of E6 coincide with the three real Lie groups mentioned above, but with a subtlety concerning the fundamental group: all adjoint forms of E6 have fundamental group Z/3Z in the sense of algebraic geometry, with Galois action as on the third roots of unity; this means that they admit exactly one triple cover (which may be trivial on the real points); the further non-compact real Lie group forms of E6 are therefore not algebraic and admit no faithful finite-dimensional representations. The compact real form of E6 as well as the noncompact forms EI=E6(6) and EIV=E6(-26) are said to be inner or of type 1E6 meaning that their class lies in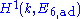
or that complex conjugation induces the trivial automorphism on the Dynkin diagram, whereas the other two real forms are said to be outer or of type 2E6.
Over finite fields, the Lang–Steinberg theorem implies that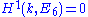
, meaning that E6 has exactly one twisted form, known as 2E6: see below.
Although they span
a six-dimensional space, it's much more symmetrical to consider them as vectors
in a six-dimensional subspace of a nine-dimensional space., (−1,1,0;0,0,0;0,0,0),, (1,0,−1;0,0,0;0,0,0),, (0,−1,1;0,0,0;0,0,0),, (0,0,0;−1,1,0;0,0,0),, (0,0,0;1,0,−1;0,0,0),, (0,0,0;0,−1,1;0,0,0),, (0,0,0;0,0,0;−1,1,0),, (0,0,0;0,0,0;1,0,−1),, (0,0,0;0,0,0;0,−1,1),
All 27 combinations of
where 
is one of 
All 27 combinations of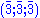
where 
is one of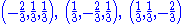 
Simple roots
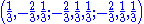
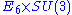as a subgroup of 
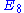, is the following:
All
permutations of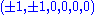
preserving the zero at the last entry,
and all of the following roots with an odd number of plus signs
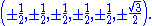
Thus the 78 generators comprise of the following subalgebras:
One choice of simple root
s for E6 is given by the rows of the following matrix: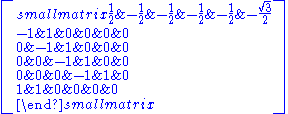
we have ordered them so that their corresponding nodes in the Dynkin diagram are ordered from left to right (in the diagram depicted above) with the side node last.
of E6 is of order 51840: it is the automorphism
group of the unique simple group
of order 25920 (which can be described as any of: PSU4(2), PSΩ6−(2), PSp4(3) or PSΩ5(3)).
Other maximal subalgebras which have an importance in physics (see below) and can be read off the Dynkin diagram, are the algebras of SO(10) × U(1) and SU(6) × SU(2).
In addition to the 78-dimensional adjoint representation, there are two dual 27-dimensional "vector" representations.
The characters of finite dimensional representations of the real and complex Lie algebras and Lie groups are all given by the Weyl character formula
. The dimensions of the smallest irreducible representations are :
The underlined terms in the sequence above are the dimensions of those irreducible representations possessed by the adjoint form of E6 (equivalently, those whose weights belong to the root lattice of E6), whereas the full sequence gives the dimensions of the irreducible representations of the simply connected form of E6.
The symmetry of the Dynkin diagram of E6 explains why many dimensions occur twice, the corresponding representations being related by the non-trivial outer automorphism; however, there are sometimes even more representations than this, such as four of dimension 351, two of which are fundamental and two of which are not.
The fundamental representation
s have dimensions 27, 351, 2925, 351, 27 and 78 (corresponding to the seven nodes in the Dynkin diagram in the order chosen for the Cartan matrix above, i.e., the nodes are read in the five-node chain first, with the last node being connected to the middle one).
of the roots of E6. It therefore exists in 6 dimensions; its symmetry group
contains the Coxeter group
for E6 as an index
2 subgroup.
The points over a finite field
with q elements of the (split) algebraic group E6 (see above), whether of the adjoint (centerless) or simply connected form (its algebraic universal cover), give a finite Chevalley group
. This is closely connected to the group written E6(q), however there is ambiguity in this notation, which can stand for several things:
From the finite group perspective, the relation between these three groups, which is quite analogous to that between SLn(q), PGLn(q) and PSLn(q), can be summarized as follows: E6(q) is simple for any q, E6,sc(q) is its Schur cover
, and E6,ad(q) lies in its automorphism group; furthermore, when q−1 is not divisible by 3, all three coincide, and otherwise (when q is congruent to 1 mod 3), the Schur multiplier of E6(q) is 3 and E6(q) is of index 3 in E6,ad(q), which explains why E6,sc(q) and E6,ad(q) are often written as 3·E6(q) and E6(q)·3. From the algebraic group perspective, it is less common for E6(q) to refer to the finite simple group, because the latter is not in a natural way the set of points of an algebraic group over Fq unlike E6,sc(q) and E6,ad(q).
Beyond this “split” (or “untwisted”) form of E6, there is also one other form of E6 over the finite field Fq, known as 2E6, which is obtained by twisting by the non-trivial automorphism of the Dynkin diagram of E6. Concretely, 2E6(q), which is known as a Steinberg group, can be seen as the subgroup of E6(q2) fixed by the composition of the non-trivial diagram automorphism and the non-trivial field automorphism of Fq2. Twisting does not change the fact that the algebraic fundamental group of 2E6,ad is Z/3Z, but it does change those q for which the covering of 2E6,ad by 2E6,sc is non-trivial on the Fq-points. Precisely: 2E6,sc(q) is a covering of 2E6(q), and 2E6,ad(q) lies in its automorphism group; when q+1 is not divisible by 3, all three coincide, and otherwise (when q is congruent to 2 mod 3), the degree of 2E6,sc(q) over 2E6(q) is 3 and 2E6(q) is of index 3 in 2E6,ad(q), which explains why 2E6,sc(q) and 2E6,ad(q) are often written as 3·2E6(q) and 2E6(q)·3.
Two notational issues should be raised concerning the groups 2E6(q). One is that this is sometimes written 2E6(q2), a notation which has the advantage of transposing more easily to the Suzuki and Ree groups, but the disadvantage of deviating from the notation for the Fq-points of an algebraic group. Another is that whereas 2E6,sc(q) and 2E6,ad(q) are the Fq-points of an algebraic group, the group in question also depends on q (e.g., the points over Fq2 of the same group are the untwisted E6,sc(q2) and E6,ad(q2)).
The groups E6(q) and 2E6(q) are simple for any q, and they constitute two of the infinite families addressed by the classification of finite simple groups
. Their number of elements is given by the formula :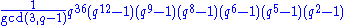
for E6(q), and
for 2E6(q). The order of E6,sc(q) or E6,ad(q) (both are equal) can be obtained by removing the dividing factor gcd(3,q−1) from the first formula , and the order of 2E6,sc(q) or 2E6,ad(q) (both are equal) can be obtained by removing the dividing factor gcd(3,q+1) from the second .
The Schur multiplier of E6(q) is always gcd(3,q−1) (i.e., E6,sc(q) is its Schur cover). The Schur multiplier of 2E6(q) is gcd(3,q+1) (i.e., 2E6,sc(q) is its Schur cover) outside of the exceptional case q=2 where it is 22·3 (i.e., there is an additional 22-fold cover). The outer automorphism group of E6(q) is the product of the diagonal automorphism group Z/gcd(3,q−1)Z (given by the action of E6,ad(q)), the group Z/2Z of diagram automorphisms, and the group of field automorphisms (i.e., cyclic of order f if q=pf where p is prime). The outer automorphism group of 2E6(q) is the product of the diagonal automorphism group Z/gcd(3,q+1)Z (given by the action of 2E6,ad(q)) and the group of field automorphisms (i.e., cyclic of order f if q=pf where p is prime).
in five dimensions, which is a dimensional reduction
from 11 dimensional supergravity, admits an E6 bosonic global symmetry and an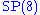
bosonic local symmetry. The fermions are in representations of 
, the gauge fields are in a representation of E6, and the scalars are in a representation of both (Gravitons are singlet
s with respect to both). Physical states are in representations of the coset
.
In grand unification theories
, E6 appears as a possible gauge group which, after its breaking
, gives rise to the
gauge group of the standard model
(also see Importance in physics of E8).
One way of achieving this is through breaking to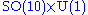
. The adjoint 78 representation breaks, as explained above, into an adjoint 
, spinor 
and 
as well as a singlet of the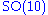 
subalgebra. Including the 
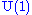charge we have
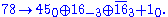
Where the subscript denotes the
charge.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, E6 is the name of some closely related Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, linear algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s or their Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s
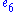, all of which have dimension 78; the same notation E6 is used for the corresponding root lattice, which has rank 6. The designation E6 comes from the Cartan–Killing classification of the complex simple Lie algebras, which fall into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled E6, E7, E8E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
, F4, and G2. The E6 algebra is thus one of the five exceptional cases.
The fundamental group of the complex form, compact real form, or any algebraic version of E6 is the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z/3Z, and its outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
is the cyclic group Z/2Z. Its fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
is 27-dimensional (complex), and a basis is given by the 27 lines on a cubic surface. The dual representation
Dual representation
In mathematics, if G is a group and ρ is a linear representation of it on the vector space V, then the dual representation is defined over the dual vector space as follows:...
, which is inequivalent, is also 27-dimensional.
In particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, E6 plays a role in some grand unified theories.
Real and complex forms
There is a unique complex Lie algebra of type E6, corresponding to a complex group of complex dimension 78. The complex adjoint Lie group E6 of complex dimensionComplex dimension
In mathematics, complex dimension usually refers to the dimension of a complex manifold M, or complex algebraic variety V. If the complex dimension is d, the real dimension will be 2d...
78 can be considered as a simple real Lie group of real dimension 156. This has fundamental group Z/3Z, has maximal compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subgroup the compact form (see below) of E6, and has an outer automorphism group non-cyclic of order 4 generated by complex conjugation and by the outer automorphism which already exists as a complex automorphism.
As well as the complex Lie group of type E6, there are five real forms of the Lie algebra, and correspondingly five real forms of the group with trivial center (all of which have an algebraic double cover, and three of which have further non-algebraic covers, giving further real forms), all of real dimension 78, as follows:
- The compact form (which is usually the one meant if no other information is given), which has fundamental group Z/3Z and outer automorphism group Z/2Z.
- The split form, sometimes known as EI or E6(6), which has maximal compact subgroup Sp4/(±1), fundamental group of order 2 and outer automorphism group of order 2.
- The quasi-split but non-split form, sometimes known as EII or E6(2), which has maximal compact subgroup SU2·SU6/(center), fundamental group cyclic of order 6 and outer automorphism group of order 2.
- A form sometimes known as EIII or E6(-14), which has maximal compact subgroup SO2·Spin10/(center), fundamental group Z and trivial outer automorphism group.
- A form sometimes known as EIV or E6(-26), which has maximal compact subgroup F4, trivial fundamental group cyclic and outer automorphism group of order 2.
A certain noncompact real form of E6 is the group of collineations (line-preserving transformations) of the octonionic projective plane OP2. It is also the group of determinant-preserving linear transformations of the exceptional Jordan algebra
Jordan algebra
In abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
. The exceptional Jordan algebra is 27-dimensional, which explains why the compact real form of E6 has a 27-dimensional complex representation. The compact real form of E6 is the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of a 32-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
known as the 'bioctonionic projective plane'.
E6 as an algebraic group
By means of a Chevalley basisChevalley basis
In mathematics, a Chevalley basis for a simple complex Lie algebra isa basis constructed by Claude Chevalley with the property that all structure constants are integers...
for the Lie algebra, one can define E6 as a linear algebraic group over the integers and, consequently, over any commutative ring and in particular over any field: this defines the so-called split (sometimes also known as “untwisted”) adjoint form of E6. Over an algebraically closed field, this and its triple cover are the only forms; however, over other fields, there are often many other forms, or “twists” of E6, which are classified in the general framework of Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
(over a perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
k) by the set
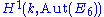which, because the Dynkin diagram of E6 (see below) has automorphism group Z/2Z, maps to 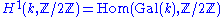with kernel .Over the field of real numbers, the real component of the identity of these algebraically twisted forms of E6 coincide with the three real Lie groups mentioned above, but with a subtlety concerning the fundamental group: all adjoint forms of E6 have fundamental group Z/3Z in the sense of algebraic geometry, with Galois action as on the third roots of unity; this means that they admit exactly one triple cover (which may be trivial on the real points); the further non-compact real Lie group forms of E6 are therefore not algebraic and admit no faithful finite-dimensional representations. The compact real form of E6 as well as the noncompact forms EI=E6(6) and EIV=E6(-26) are said to be inner or of type 1E6 meaning that their class lies in
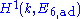or that complex conjugation induces the trivial automorphism on the Dynkin diagram, whereas the other two real forms are said to be outer or of type 2E6.Over finite fields, the Lang–Steinberg theorem implies that
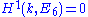, meaning that E6 has exactly one twisted form, known as 2E6: see below.Roots of E6
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
a six-dimensional space, it's much more symmetrical to consider them as vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
in a six-dimensional subspace of a nine-dimensional space., (−1,1,0;0,0,0;0,0,0),, (1,0,−1;0,0,0;0,0,0),, (0,−1,1;0,0,0;0,0,0),, (0,0,0;−1,1,0;0,0,0),, (0,0,0;1,0,−1;0,0,0),, (0,0,0;0,−1,1;0,0,0),, (0,0,0;0,0,0;−1,1,0),, (0,0,0;0,0,0;1,0,−1),, (0,0,0;0,0,0;0,−1,1),
All 27 combinations of
where is one of All 27 combinations of
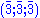where is one of 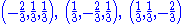Simple roots
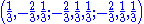
An alternative description
An alternative (6-dimensional) description of the root system, which is useful in considering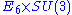 as a subgroup of 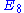, is the following:All
permutations of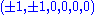 preserving the zero at the last entry,and all of the following roots with an odd number of plus signs
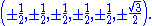
Thus the 78 generators comprise of the following subalgebras:
- A 45-dimensional
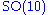subalgebra, including the above 
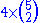generators plus the five Cartan generators corresponding to the first five entries. - Two 16-dimensional subalgebras that transform as a Weyl spinor of
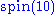and its complex conjugate. These have a non-zero last entry. - 1 generator which is their chirality generator, and is the sixth Cartan generator.
One choice of simple root
Simple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s for E6 is given by the rows of the following matrix:
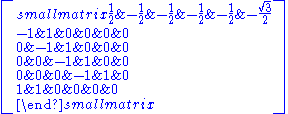
we have ordered them so that their corresponding nodes in the Dynkin diagram are ordered from left to right (in the diagram depicted above) with the side node last.
Weyl group
The Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of E6 is of order 51840: it is the automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
group of the unique simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
of order 25920 (which can be described as any of: PSU4(2), PSΩ6−(2), PSp4(3) or PSΩ5(3)).
Cartan matrix
Important subalgebras and representations
The Lie algebra E6 has an F4 subalgebra, which is the fixed subalgebra of an outer automorphism, and an SU(3) × SU(3) × SU(3) subalgebra.Other maximal subalgebras which have an importance in physics (see below) and can be read off the Dynkin diagram, are the algebras of SO(10) × U(1) and SU(6) × SU(2).
In addition to the 78-dimensional adjoint representation, there are two dual 27-dimensional "vector" representations.
The characters of finite dimensional representations of the real and complex Lie algebras and Lie groups are all given by the Weyl character formula
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
. The dimensions of the smallest irreducible representations are :
- 1, 27 (twice), 78, 351 (four times), 650, 1728 (twice), 2430, 2925, 3003 (twice), 5824 (twice), 7371 (twice), 7722 (twice), 17550 (twice), 19305 (four times), 34398 (twice), 34749, 43758, 46332 (twice), 51975 (twice), 54054 (twice), 61425 (twice), 70070, 78975 (twice), 85293, 100386 (twice), 105600, 112320 (twice), 146432 (twice), 252252 (twice), 314496 (twice), 359424 (four times), 371800 (twice), 386100 (twice), 393822 (twice), 412776 (twice), 442442 (twice)…
The underlined terms in the sequence above are the dimensions of those irreducible representations possessed by the adjoint form of E6 (equivalently, those whose weights belong to the root lattice of E6), whereas the full sequence gives the dimensions of the irreducible representations of the simply connected form of E6.
The symmetry of the Dynkin diagram of E6 explains why many dimensions occur twice, the corresponding representations being related by the non-trivial outer automorphism; however, there are sometimes even more representations than this, such as four of dimension 351, two of which are fundamental and two of which are not.
The fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
s have dimensions 27, 351, 2925, 351, 27 and 78 (corresponding to the seven nodes in the Dynkin diagram in the order chosen for the Cartan matrix above, i.e., the nodes are read in the five-node chain first, with the last node being connected to the middle one).
E6 polytope
The E6 polytope is the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the roots of E6. It therefore exists in 6 dimensions; its symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
contains the Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
for E6 as an index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 subgroup.
Chevalley and Steinberg groups of type E6 and 2E6
The groups of type E6 over arbitrary fields (in particular finite fields) were introduced by .The points over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with q elements of the (split) algebraic group E6 (see above), whether of the adjoint (centerless) or simply connected form (its algebraic universal cover), give a finite Chevalley group
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
. This is closely connected to the group written E6(q), however there is ambiguity in this notation, which can stand for several things:
- the finite group consisting of the points over Fq of the simply connected form of E6 (for clarity, this can be written E6,sc(q) or
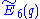, and is known as the “universal” Chevalley group of type E6 over Fq), - (rarely) the finite group consisting of the points over Fq of the adjoint form of E6 (for clarity, this can be written E6,ad(q), and is known as the “adjoint” Chevalley group of type E6 over Fq), or
- the finite group which is the image of the natural map from the former to the latter: this is what will be denoted by E6(q) in the following, as is most common in texts dealing with finite groups.
From the finite group perspective, the relation between these three groups, which is quite analogous to that between SLn(q), PGLn(q) and PSLn(q), can be summarized as follows: E6(q) is simple for any q, E6,sc(q) is its Schur cover
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
, and E6,ad(q) lies in its automorphism group; furthermore, when q−1 is not divisible by 3, all three coincide, and otherwise (when q is congruent to 1 mod 3), the Schur multiplier of E6(q) is 3 and E6(q) is of index 3 in E6,ad(q), which explains why E6,sc(q) and E6,ad(q) are often written as 3·E6(q) and E6(q)·3. From the algebraic group perspective, it is less common for E6(q) to refer to the finite simple group, because the latter is not in a natural way the set of points of an algebraic group over Fq unlike E6,sc(q) and E6,ad(q).
Beyond this “split” (or “untwisted”) form of E6, there is also one other form of E6 over the finite field Fq, known as 2E6, which is obtained by twisting by the non-trivial automorphism of the Dynkin diagram of E6. Concretely, 2E6(q), which is known as a Steinberg group, can be seen as the subgroup of E6(q2) fixed by the composition of the non-trivial diagram automorphism and the non-trivial field automorphism of Fq2. Twisting does not change the fact that the algebraic fundamental group of 2E6,ad is Z/3Z, but it does change those q for which the covering of 2E6,ad by 2E6,sc is non-trivial on the Fq-points. Precisely: 2E6,sc(q) is a covering of 2E6(q), and 2E6,ad(q) lies in its automorphism group; when q+1 is not divisible by 3, all three coincide, and otherwise (when q is congruent to 2 mod 3), the degree of 2E6,sc(q) over 2E6(q) is 3 and 2E6(q) is of index 3 in 2E6,ad(q), which explains why 2E6,sc(q) and 2E6,ad(q) are often written as 3·2E6(q) and 2E6(q)·3.
Two notational issues should be raised concerning the groups 2E6(q). One is that this is sometimes written 2E6(q2), a notation which has the advantage of transposing more easily to the Suzuki and Ree groups, but the disadvantage of deviating from the notation for the Fq-points of an algebraic group. Another is that whereas 2E6,sc(q) and 2E6,ad(q) are the Fq-points of an algebraic group, the group in question also depends on q (e.g., the points over Fq2 of the same group are the untwisted E6,sc(q2) and E6,ad(q2)).
The groups E6(q) and 2E6(q) are simple for any q, and they constitute two of the infinite families addressed by the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
. Their number of elements is given by the formula :
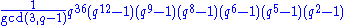
for E6(q), and
for 2E6(q). The order of E6,sc(q) or E6,ad(q) (both are equal) can be obtained by removing the dividing factor gcd(3,q−1) from the first formula , and the order of 2E6,sc(q) or 2E6,ad(q) (both are equal) can be obtained by removing the dividing factor gcd(3,q+1) from the second .
The Schur multiplier of E6(q) is always gcd(3,q−1) (i.e., E6,sc(q) is its Schur cover). The Schur multiplier of 2E6(q) is gcd(3,q+1) (i.e., 2E6,sc(q) is its Schur cover) outside of the exceptional case q=2 where it is 22·3 (i.e., there is an additional 22-fold cover). The outer automorphism group of E6(q) is the product of the diagonal automorphism group Z/gcd(3,q−1)Z (given by the action of E6,ad(q)), the group Z/2Z of diagram automorphisms, and the group of field automorphisms (i.e., cyclic of order f if q=pf where p is prime). The outer automorphism group of 2E6(q) is the product of the diagonal automorphism group Z/gcd(3,q+1)Z (given by the action of 2E6,ad(q)) and the group of field automorphisms (i.e., cyclic of order f if q=pf where p is prime).
Importance in physics
N=8 supergravitySupergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
in five dimensions, which is a dimensional reduction
Dimensional reduction
In physics, a theory in D spacetime dimensions can be redefined in a lower number of dimensions d, by taking all the fields to be independent of the location in the extra D − d dimensions....
from 11 dimensional supergravity, admits an E6 bosonic global symmetry and an
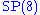bosonic local symmetry. The fermions are in representations of , the gauge fields are in a representation of E6, and the scalars are in a representation of both (Gravitons are singletSinglet
A pair of spin-1/2 particles can be combined to form one of three states of total spin 1 called the triplet, or a state of spin 0 which is called the singlet. In theoretical physics, a singlet usually refers to a one-dimensional representation...
s with respect to both). Physical states are in representations of the coset
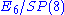.In grand unification theories
Grand unification theory
The term Grand Unified Theory, often abbreviated as GUT, refers to any of several similar candidate models in particle physics in which at high-energy, the three gauge interactions of the Standard Model which define the electromagnetic, weak, and strong interactions, are merged into one single...
, E6 appears as a possible gauge group which, after its breaking
Symmetry breaking
Symmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
, gives rise to the
gauge group of the standard modelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
(also see Importance in physics of E8).
One way of achieving this is through breaking to
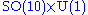. The adjoint 78 representation breaks, as explained above, into an adjoint , spinor and as well as a singlet of the 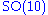subalgebra. Including the 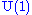charge we have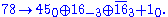Where the subscript denotes the
charge.