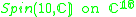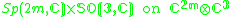Prehomogeneous vector space
Encyclopedia
In mathematics, a prehomogeneous vector space (PVS) is a finite-dimensional vector space
V together with a subgroup G of GL(V) such that G has an open dense orbit in V. Prehomogeneous vector spaces were introduced by Mikio Sato
in 1970 and have many applications in geometry
, number theory
and analysis
, as well as representation theory
. The irreducible PVS were classified by Sato and Tatsuo Kimura in 1977, up to a transformation known as "castling". They are subdivided into two types, according to whether the semisimple part of G acts prehomogeneously or not. If it doesn't then there is a homogeneous polynomial on V which is invariant under the semisimple part of G.
and V is a rational representation of G which has a (nonempty) open orbit in the Zariski topology
. However, PVS can also be studied from the point of view of Lie theory: for instance, in Knapp (2002), G is a complex Lie group and V is a holomorphic representation of G with an open dense orbit. The two approaches are essentially the same, and it is also interesting to study the theory over the real numbers. We assume, for simplicity of notation, that the action of G on V is a faithful representation
. We can then identify G with its image in GL(V), although in practice it is sometimes convenient to let G be a covering group.
Although prehomogeneous vector spaces do not necessarily decompose into direct sums of irreducibles, it is natural to study the irreducible PVS (i.e., when V is an irreducible representation of G). In this case, a theorem of Élie Cartan
shows that
is a reductive group
, with a centre that is at most one-dimensional. This, together with the obvious dimensional restriction
is the key ingredient in the Sato–Kimura classification.
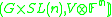is a PVS if and only if 
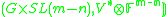is a PVS.
The proof is to observe that both conditions are equivalent to there being an open dense orbit of the action of G on the Grassmannian
of
n-planes in V, because this is isomorphic to the Grassmannian
of (m-n)-planes in V*.
(In the case that G is reductive, the pair (G,V) is equivalent to the pair (G, V*) by an automorphism of G.)
This transformation of PVS is called castling
. Given a PVS V, a new PVS can be obtained by tensoring V with IF and castling. By repeating this process, and regrouping tensor products, many new examples can be obtained, which are said to be "castling-equivalent". Thus PVS can be grouped into castling equivalence classes. Sato and Kimura show that in each such class, there is essentially one PVS of minimal dimension, which they call "reduced", and they classify the reduced irreducible PVS.
This makes it possible to restrict attention to semisimple G ≤ SL(V) and split the classification as follows:
However, it turns out that the classification is much shorter, if one allows not just products with GL(1), but also with SL(n) and GL(n). This is quite natural in terms of the castling transformation discussed previously. Thus we wish to classify irreducible reduced PVS in terms of semisimple G ≤ SL(V) and n ≥ 1 such that either:
In the latter case, there is a homogeneous polynomial
which separates the G×GL(n) orbits into G×SL(n) orbits.
This has an interpretation in terms of the grassmannian Grn(V) of n-planes in V (at least for n ≤ dim V). In both cases G acts on Grn(V) with a dense open orbit U. In the first case the complement Grn(V)-U has codimension
≥ 2; in the second case it is a divisor
of some degree d, and the relative invariant is a homogeneous polynomial of degree nd.
In the following, the classification list will be presented over the complex numbers.
* Strictly speaking, we must restrict to n ≤ (dim V)/2 to obtain a reduced example.
Type 2
Both of these examples are PVS only for n=1.
of the isotropy group rather than the isotropy group itself.
Here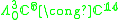
denotes the space of 3-forms whose contraction with the given symplectic form is zero.
However, there is a general explanation why most of the pairs (G,V) in the classification are prehomogeneous, in terms of isotropy representations of generalized flag varieties. Indeed, in 1974, Richardson
observed that if H is a semisimple Lie group with a parabolic subgroup P, then the action of P on the nilradical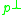
of its Lie algebra has a dense open orbit. This shows in particular (and was noted independently by Vinberg in 1975) that the Levi factor G of P acts prehomogeneously on 
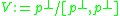. Almost all of the examples in the classification can be obtained by applying this construction with P a maximal parabolic subgroup of a simple Lie group H: these are classified by connected Dynkin diagrams with one distinguished node.
Another example concerns the prehomogeneous vector spaces with a cubic relative invariant. By the Sato-Kimura classification, there are essentially four such examples, and they all come from complexified isotropy representations of hermitian symmetric space
s for a larger group H (i.e., G is the semisimple part of the stabilizer of a point, and V is the corresponding tangent
representation).
In each case a generic point in V identifies it with the complexification of a Jordan algebra
of 3 x 3 hermitian matrices (over the division algebra
s R, C, H and O respectively) and the cubic relative invariant is identified with a suitable determinant. The isotropy algebra of such a generic point, the Lie algebra of G and the Lie algebra of H give the complexifications of the first three rows of the Freudenthal magic square
.
Other Hermitian symmetric spaces yields prehomogeneous vector spaces whose generic points define Jordan algebras in a similar way.
The Jordan algebra J(m−1) in the last row is the spin factor (which is the vector space Rm−1 ⊕ R, with a Jordan algebra structure defined using the inner product on Rm−1). It reduces to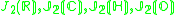
for m= 3, 4, 6 and 10 respectively.
The relation between hermitian symmetric spaces and Jordan algebras can be explained using Jordan triple systems.
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V together with a subgroup G of GL(V) such that G has an open dense orbit in V. Prehomogeneous vector spaces were introduced by Mikio Sato
Mikio Sato
is a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
in 1970 and have many applications in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
, as well as representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. The irreducible PVS were classified by Sato and Tatsuo Kimura in 1977, up to a transformation known as "castling". They are subdivided into two types, according to whether the semisimple part of G acts prehomogeneously or not. If it doesn't then there is a homogeneous polynomial on V which is invariant under the semisimple part of G.
Setting
In the setting of Sato, G is an algebraic groupAlgebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
and V is a rational representation of G which has a (nonempty) open orbit in the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
. However, PVS can also be studied from the point of view of Lie theory: for instance, in Knapp (2002), G is a complex Lie group and V is a holomorphic representation of G with an open dense orbit. The two approaches are essentially the same, and it is also interesting to study the theory over the real numbers. We assume, for simplicity of notation, that the action of G on V is a faithful representation
Faithful representation
In mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ.In more abstract language, this means...
. We can then identify G with its image in GL(V), although in practice it is sometimes convenient to let G be a covering group.
Although prehomogeneous vector spaces do not necessarily decompose into direct sums of irreducibles, it is natural to study the irreducible PVS (i.e., when V is an irreducible representation of G). In this case, a theorem of Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
shows that
- G ≤ GL(V)
is a reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
, with a centre that is at most one-dimensional. This, together with the obvious dimensional restriction
- dim G ≥ dim V,
is the key ingredient in the Sato–Kimura classification.
Castling
The classification of PVS is complicated by the following fact. Suppose m > n > 0 and V is an m-dimensional representation of G over a field IF. Then: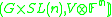 is a PVS if and only if 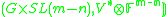is a PVS.The proof is to observe that both conditions are equivalent to there being an open dense orbit of the action of G on the Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
of
n-planes in V, because this is isomorphic to the Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
of (m-n)-planes in V*.
(In the case that G is reductive, the pair (G,V) is equivalent to the pair (G, V*) by an automorphism of G.)
This transformation of PVS is called castling
Castling
Castling is a special move in the game of chess involving the king and either of the original rooks of the same color. It is the only move in chess in which a player moves two pieces at the same time. Castling consists of moving the king two squares towards a rook on the player's first rank, then...
. Given a PVS V, a new PVS can be obtained by tensoring V with IF and castling. By repeating this process, and regrouping tensor products, many new examples can be obtained, which are said to be "castling-equivalent". Thus PVS can be grouped into castling equivalence classes. Sato and Kimura show that in each such class, there is essentially one PVS of minimal dimension, which they call "reduced", and they classify the reduced irreducible PVS.
Classification
The classification of irreducible reduced PVS (G,V) splits into two cases: those for which G is semisimple, and those for which it is reductive with one-dimensional centre. If G is semisimple, it is (perhaps a covering of) a subgroup of SL(V), and hence G×GL(1) acts prehomogenously on V, with one-dimensional centre. We exclude such trivial extensions of semisimple PVS from the PVS with one-dimensional center. In other words, in the case that G has one-dimensional center, we assume that the semisimple part does not act prehomogeneously; it follows that there is a relative invariant, i.e., a function invariant under the semisimple part of G, which is homogeneous of a certain degree d.This makes it possible to restrict attention to semisimple G ≤ SL(V) and split the classification as follows:
- (G,V) is a PVS;
- (G,V) is not a PVS, but (G×GL(1),V) is.
However, it turns out that the classification is much shorter, if one allows not just products with GL(1), but also with SL(n) and GL(n). This is quite natural in terms of the castling transformation discussed previously. Thus we wish to classify irreducible reduced PVS in terms of semisimple G ≤ SL(V) and n ≥ 1 such that either:
-
is a PVS; -
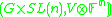is not a PVS, but 
is.
In the latter case, there is a homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
which separates the G×GL(n) orbits into G×SL(n) orbits.
This has an interpretation in terms of the grassmannian Grn(V) of n-planes in V (at least for n ≤ dim V). In both cases G acts on Grn(V) with a dense open orbit U. In the first case the complement Grn(V)-U has codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
≥ 2; in the second case it is a divisor
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
of some degree d, and the relative invariant is a homogeneous polynomial of degree nd.
In the following, the classification list will be presented over the complex numbers.
General examples
| G | V | Type 1 | Type 2 | Type 2 isotropy group | Degree |
|---|---|---|---|---|---|
 |
 |
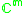n ≥ m+1 | n = m |  |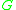
m |
 |
 |
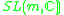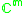m-1 ≥ n ≥ 1* | |||
 |
 |
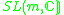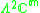m odd, n = 1,2 | m even, n = 1 |  |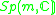
m/2 |
 |
 |
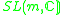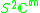n = 1 |  |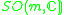
m | |
 |
 |
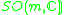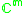m-1 ≥ n ≥ 1* |  |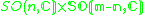
2 | |
 |
 |
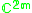2m-1 ≥ n ≥ 1*, n odd | 2m-1 ≥ n ≥ 1*, n even |  |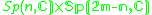
1 |
* Strictly speaking, we must restrict to n ≤ (dim V)/2 to obtain a reduced example.
Irregular examples
Type 1
Type 2
Both of these examples are PVS only for n=1.
Remaining examples
The remaining examples are all type 2. To avoid discussing the finite groups appearing, the lists present the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of the isotropy group rather than the isotropy group itself.
| G | V | n | Isotropy algebra | Degree |
|---|---|---|---|---|
 |
 |
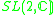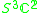1 | 0 | 4 |
 |
 |
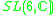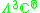1 |  |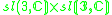
4 |
 |
 |
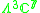1 |  |
7 |
 |
 |
1 |  |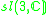
16 |
 |
 |
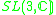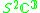2 | 0 | 6 |
 |
 |
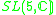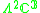3,4 |  |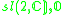
5,10 |
 |
 |
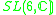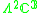2 |  |
6 |
 |
 |
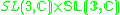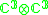2 |  |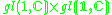
6 |
 |
 |
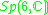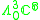1 |  |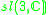
4 |
 |
 |
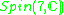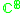1,2,3 |  |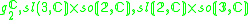
2,2,2 |
 |
 |
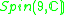1 |  |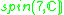
2 |
 |
 |
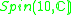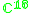2,3 |  |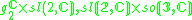
2,4 |
 |
 |
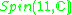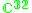1 |  |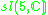
4 |
 |
 |
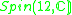1 |  |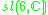
4 |
 |
 |
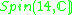1 |  |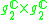
8 |
 |
 |
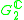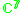1,2 |  |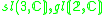
2,2 |
 |
 |
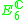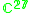1,2 |  |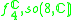
3,6 |
 |
 |
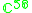1 |  |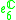
4 |
Here
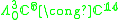denotes the space of 3-forms whose contraction with the given symplectic form is zero.Proofs
Sato and Kimura establish this classification by producing a list of possible irreducible prehomogeneous (G,V), using the fact that G is reductive and the dimensional restriction. They then check whether each member of this list is prehomogeneous or not.However, there is a general explanation why most of the pairs (G,V) in the classification are prehomogeneous, in terms of isotropy representations of generalized flag varieties. Indeed, in 1974, Richardson
Roger Wolcott Richardson
Roger Wolcott Richardson was a mathematician noted for his work in representation theory and geometry. He was born in Baton Rouge, Louisiana, and educated at Louisiana State University, Harvard University and University of Michigan, Ann Arbor where he obtained a Ph.D. under the supervision of Hans...
observed that if H is a semisimple Lie group with a parabolic subgroup P, then the action of P on the nilradical
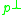of its Lie algebra has a dense open orbit. This shows in particular (and was noted independently by Vinberg in 1975) that the Levi factor G of P acts prehomogeneously on 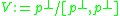. Almost all of the examples in the classification can be obtained by applying this construction with P a maximal parabolic subgroup of a simple Lie group H: these are classified by connected Dynkin diagrams with one distinguished node.Applications
One reason that PVS are interesting is that they classify generic objects that arise in G-invariant situations. For example, if G=GL(7), then the above tables show that there are generic 3-forms under the action of G, and the stabilizer of such a 3-form is isomorphic to the exceptional Lie group G2.Another example concerns the prehomogeneous vector spaces with a cubic relative invariant. By the Sato-Kimura classification, there are essentially four such examples, and they all come from complexified isotropy representations of hermitian symmetric space
Hermitian symmetric space
In mathematics, a Hermitian symmetric space is a Kähler manifold M which, as a Riemannian manifold, is a Riemannian symmetric space. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian...
s for a larger group H (i.e., G is the semisimple part of the stabilizer of a point, and V is the corresponding tangent
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
representation).
In each case a generic point in V identifies it with the complexification of a Jordan algebra
Jordan algebra
In abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
of 3 x 3 hermitian matrices (over the division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
s R, C, H and O respectively) and the cubic relative invariant is identified with a suitable determinant. The isotropy algebra of such a generic point, the Lie algebra of G and the Lie algebra of H give the complexifications of the first three rows of the Freudenthal magic square
Freudenthal magic square
In mathematics, the Freudenthal magic square is a construction relating several Lie groups. It is named after Hans Freudenthal and Jacques Tits, who developed the idea independently. It associates a Lie group to a pair of division algebras A, B...
.
| H | G | V | Isotropy algebra | Jordan algebra |
|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
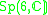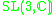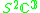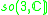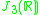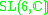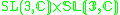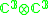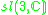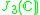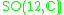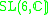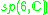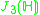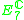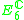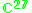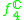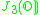Other Hermitian symmetric spaces yields prehomogeneous vector spaces whose generic points define Jordan algebras in a similar way.
| H | G | V | Isotropy algebra | Jordan algebra |
|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
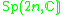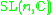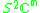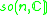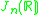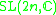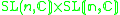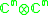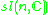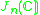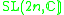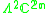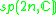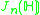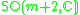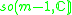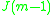The Jordan algebra J(m−1) in the last row is the spin factor (which is the vector space Rm−1 ⊕ R, with a Jordan algebra structure defined using the inner product on Rm−1). It reduces to
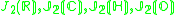for m= 3, 4, 6 and 10 respectively.The relation between hermitian symmetric spaces and Jordan algebras can be explained using Jordan triple systems.