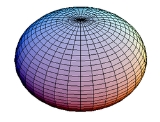
Figure of the Earth
Encyclopedia
The expression figure of the Earth has various meanings in geodesy
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
according to the way it is used and the precision with which the Earth's size and shape is to be defined. The actual topographic surface is most apparent with its variety of land forms and water areas. This is, in fact, the surface on which actual Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
measurements are made. It is not suitable, however, for exact mathematical computations, because the formulas which would be required to take the irregularities into account would necessitate a prohibitive amount of computations. The topographic surface is generally the concern of topographers and hydrographers.
The Pythagorean
Pythagoreanism
Pythagoreanism was the system of esoteric and metaphysical beliefs held by Pythagoras and his followers, the Pythagoreans, who were considerably influenced by mathematics. Pythagoreanism originated in the 5th century BCE and greatly influenced Platonism...
concept of a spherical Earth
Spherical Earth
The concept of a spherical Earth dates back to ancient Greek philosophy from around the 6th century BC, but remained a matter of philosophical speculation until the 3rd century BC when Hellenistic astronomy established the spherical shape of the earth as a physical given...
offers a simple surface which is mathematically easy to deal with. Many astronomical and navigational computations use it as a surface representing the Earth. While the sphere is a close approximation of the true figure of the Earth and satisfactory for many purposes, to the geodesists interested in the measurement of long distances—spanning continents and oceans—a more exact figure is necessary. Closer approximations range from modelling the shape of the entire Earth as an oblate spheroid or an oblate ellipsoid, to the use of spherical harmonic
Spherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s or local approximations in terms of local reference ellipsoid
Reference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
s. The idea of a planar or flat surface for Earth, however, is still acceptable for surveys of small areas, as local topography
Topography
Topography is the study of Earth's surface shape and features or those ofplanets, moons, and asteroids...
is more important than the curvature. Plane-table surveys are made for relatively small areas, and no account is taken of the curvature of the Earth. A survey of a city would likely be computed as though the Earth were a plane surface the size of the city. For such small areas, exact positions can be determined relative to each other without considering the size and shape of the total Earth.
In the mid- to late- 20th century, research across the geosciences contributed to drastic improvements in the accuracy of the Figure of the Earth. The primary utility (and the motivation for funding, mainly from the military) of this improved accuracy was to provide geographical and gravitational data for the inertial guidance systems of ballistic missile
Ballistic missile
A ballistic missile is a missile that follows a sub-orbital ballistic flightpath with the objective of delivering one or more warheads to a predetermined target. The missile is only guided during the relatively brief initial powered phase of flight and its course is subsequently governed by the...
s. This funding also drove the expansion of geoscientific disciplines, fostering the creation and growth of various geoscience departments at many universities.
Ellipsoid of revolution
Since the Earth is flattened at the poles and bulging at the equator, the geometrical figure used in geodesy to most nearly approximate Earth's shape is an oblate spheroid. An oblate spheroid, or oblate ellipsoid, is an ellipsoid of revolution obtained by rotating an ellipse about its shorter axis. A spheroid describing the figure of the Earth or other celestial bodyCelestial Body
Celestial Body is a Croatian film directed by Lukas Nola. It was released in 2000....
is called a reference ellipsoid
Reference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
. The reference ellipsoid for the Earth is called Earth ellipsoid
Earth ellipsoid
An Earth ellipsoid is a mathematical figure approximating the shape of the Earth, used as a reference frame for computations in geodesy, astronomy and the geosciences...
.
An ellipsoid of revolution is uniquely defined by two numbers-- two dimensions, or one dimension and a number representing the difference between the two dimensions. Geodesists, by convention, use the semimajor axis and flattening
Flattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
. The size is represented by the radius at the equator—the semimajor axis of the cross-sectional ellipse—and designated by the letter
 . The shape of the ellipsoid is given by the flattening,
. The shape of the ellipsoid is given by the flattening,  , which indicates how much the ellipsoid departs from spherical. (In practice, the two defining numbers are usually the equatorial radius and the reciprocal of the flattening, rather than the flattening itself; for the WGS84 spheroid used by today's GPS systems, the reciprocal of the flattening is set at 298.257223563 exactly.)
, which indicates how much the ellipsoid departs from spherical. (In practice, the two defining numbers are usually the equatorial radius and the reciprocal of the flattening, rather than the flattening itself; for the WGS84 spheroid used by today's GPS systems, the reciprocal of the flattening is set at 298.257223563 exactly.)The difference between a sphere and a reference ellipsoid for Earth is small, only about one part in 300. Historically flattening was computed from grade measurement
Grade measurement
Grade measurement is the geodetic determination of the local radius of curvature of the figure of the Earth by determining the difference in astronomical latitude between two locations on the same meridian, the metric distance between which is known....
s. Nowadays geodetic networks and satellite geodesy
Satellite geodesy
Satellite geodesy is the measurement of the form and dimensions of the Earth, the location of objects on its surface and the figure of the Earth's gravity field by means of artificial satellite techniques—geodesy by means of artificial satellites...
are used. In practice, many reference ellipsoids have been developed over the centuries from different surveys. The flattening value varies slightly from one reference ellipsoid to another, reflecting local conditions and whether the reference ellipsoid is intended to model the entire earth or only some portion of it.
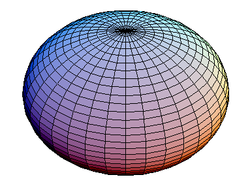
A sphere has a single radius of curvature, which is simply the radius of the sphere. More complex surfaces have radii of curvature that vary over the surface. The radius of curvature describes the radius of the sphere that best approximates the surface at that point. Oblate ellipsoids have constant radius of curvature east to west along parallels, if a graticule
Graticule
Graticule may refer to:* An oscilloscope graticule scale* Another name for the reticle pattern in an optical instrument* The grid used in the Geographic coordinate system...
is drawn on the surface, but varying curvature in any other direction. For an oblate ellipsoid, the polar radius of curvature
 is larger than the equatorial
is larger than the equatorial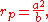
because the pole is flattened: the flatter the surface, the larger the sphere must be to approximate it. Conversely, the ellipsoid's north-south radius of curvature at the equator
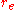 is smaller than the polar
is smaller than the polar
Historical Earth ellipsoids
The reference ellipsoid models listed below have had utility in geodetic work and many are still in use. The older ellipsoids are named for the individual who derived them and the year of development is given. In 1887 the English mathematician Col Alexander Ross ClarkeAlexander Ross Clarke
Alexander Ross Clarke was a British geodesist, primarily remembered for his work defining different reference ellipsoids approximating the shape of the geoid.Clarke was born on December 16, 1828 in Reading, Berkshire, England...
CB FRS RE was awarded the Gold Medal of the Royal Society for his work in determining the figure of the Earth. The international ellipsoid was developed by John Fillmore Hayford
John Fillmore Hayford
- References :...
in 1910 and adopted by the International Union of Geodesy and Geophysics (IUGG) in 1924, which recommended it for international use.
At the 1967 meeting of the IUGG held in Lucerne, Switzerland, the ellipsoid called GRS-67 (Geodetic Reference System
Geodetic system
Geodetic systems or geodetic data are used in geodesy, navigation, surveying by cartographers and satellite navigation systems to translate positions indicated on their products to their real position on earth....
1967) in the listing was recommended for adoption. The new ellipsoid was not recommended to replace the International Ellipsoid (1924), but was advocated for use where a greater degree of accuracy is required. It became a part of the GRS-67 which was approved and adopted at the 1971 meeting of the IUGG held in Moscow. It is used in Australia for the Australian Geodetic Datum and in South America for the South American Datum 1969.
The GRS-80 (Geodetic Reference System 1980) as approved and adopted by the IUGG at its Canberra, Australia meeting of 1979 is based on the equatorial radius (semi-major axis of Earth ellipsoid)
 , total mass
, total mass 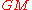 , dynamic form factor
, dynamic form factor  and angular velocity of rotation
and angular velocity of rotation  , making the inverse flattening
, making the inverse flattening 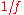 a derived quantity. The minute difference in
a derived quantity. The minute difference in  seen between GRS-80 and WGS-84 results from an unintentional truncation in the latter's defining constants: while the WGS-84 was designed to adhere closely to the GRS-80, incidentally the WGS-84 derived flattening turned out to be slightly different than the GRS-80 flattening because the normalized second degree zonal harmonic gravitational coefficient, that was derived from the GRS-80 value for J2, was truncated to 8 significant digits in the normalization process.
seen between GRS-80 and WGS-84 results from an unintentional truncation in the latter's defining constants: while the WGS-84 was designed to adhere closely to the GRS-80, incidentally the WGS-84 derived flattening turned out to be slightly different than the GRS-80 flattening because the normalized second degree zonal harmonic gravitational coefficient, that was derived from the GRS-80 value for J2, was truncated to 8 significant digits in the normalization process.An ellipsoidal model describes only the ellipsoid's geometry and a normal gravity field formula to go with it. Commonly an ellipsoidal model is part of a more encompassing geodetic datum. For example, the older ED-50 (European Datum 1950
ED50
ED 50 is a geodetic datum which was defined after World War II for the international connection of geodetic networks....
) is based on the Hayford or International Ellipsoid. WGS-84 is peculiar in that the same name is used for both the complete geodetic reference system and its component ellipsoidal model. Nevertheless the two concepts—ellipsoidal model and geodetic reference system—remain distinct.
Note that the same ellipsoid may be known by different names. It is best to mention the defining constants for unambiguous identification.
| Reference ellipsoid name | Equatorial radius (m) | Polar radius (m) | Inverse flattening | Where used |
|---|---|---|---|---|
| Maupertuis Pierre Louis Maupertuis Pierre-Louis Moreau de Maupertuis was a French mathematician, philosopher and man of letters. He became the Director of the Académie des Sciences, and the first President of the Berlin Academy of Science, at the invitation of Frederick the Great.... (1738) |
6,397,300 | 6,363,806.283 | 191 | France |
| Plessis Plessis Plessis, Plessy, du Plessis, and de Plessis are related French surnames, and may refer to:* Cardinal Richelieu, French statesman and cardinal, born Armand-Jean du Plessis, Seigneur de Richelieu... (1817) |
6,376,523.0 | 6,355,862.9333 | 308.64 | France |
| Everest George Everest Colonel Sir George Everest was a Welsh surveyor, geographer and Surveyor-General of India from 1830 to 1843.Sir George was largely responsible for completing the section of the Great Trigonometric Survey of India along the meridian arc from the south of India extending north to Nepal, a distance... (1830) |
6,377,299.365 | 6,356,098.359 | 300.80172554 | India |
| Everest 1830 Modified (1967) | 6,377,304.063 | 6,356,103.0390 | 300.8017 | West Malaysia & Singapore |
| Everest 1830 (1967 Definition) | 6,377,298.556 | 6,356,097.550 | 300.8017 | Brunei & East Malaysia |
| Airy George Biddell Airy Sir George Biddell Airy PRS KCB was an English mathematician and astronomer, Astronomer Royal from 1835 to 1881... (1830) |
6,377,563.396 | 6,356,256.909 | 299.3249646 | Britain |
| Bessel Bessel ellipsoid The Bessel ellipsoid is an important reference ellipsoid of geodesy. It is currently used by several countries for their national geodetic surveys, in Europe and on other continents, but will be replaced in the next decades by modern ellipsoids of satellite geodesy.The Bessel ellipsoid was derived... (1841) |
6,377,397.155 | 6,356,078.963 | 299.1528128 | Europe, Japan |
| Clarke Alexander Ross Clarke Alexander Ross Clarke was a British geodesist, primarily remembered for his work defining different reference ellipsoids approximating the shape of the geoid.Clarke was born on December 16, 1828 in Reading, Berkshire, England... (1866) |
6,378,206.4 | 6,356,583.8 | 294.9786982 | North America |
| Clarke Alexander Ross Clarke Alexander Ross Clarke was a British geodesist, primarily remembered for his work defining different reference ellipsoids approximating the shape of the geoid.Clarke was born on December 16, 1828 in Reading, Berkshire, England... (1878) |
6,378,190 | 6,356,456 | 293.4659980 | North America |
| Clarke Alexander Ross Clarke Alexander Ross Clarke was a British geodesist, primarily remembered for his work defining different reference ellipsoids approximating the shape of the geoid.Clarke was born on December 16, 1828 in Reading, Berkshire, England... (1880) |
6,378,249.145 | 6,356,514.870 | 293.465 | France, Africa |
| Helmert Friedrich Robert Helmert Friedrich Robert Helmert was a German geodesist and an important writer on the theory of errors.Helmert was born in Freiberg, Kingdom of Saxony. After schooling in Freiberg and Dresden, he entered the Polytechnische Schule, now Technische Universität, in Dresden to study engineering science in 1859... (1906) |
6,378,200 | 6,356,818.17 | 298.3 | |
| Hayford John Fillmore Hayford - References :... (1910) |
6,378,388 | 6,356,911.946 | 297 | USA |
| International (1924) | 6,378,388 | 6,356,911.946 | 297 | Europe |
| NAD 27 (1927) | 6,378,206.4 | 6,356,583.800 | 294.978698208 | North America |
| Krassovsky Feodosy Krasovsky Feodosy Nikolaevich Krasovsky was a Russian and later Soviet astronomer and geodesist. He was born in Galich. In 1900 he graduated from the Mezhevoy Institute in Moscow; in 1907 he began working as a lecturer there.-Research work:... (1940) |
6,378,245 | 6,356,863.019 | 298.3 | USSR |
| WGS66 (1966) | 6,378,145 | 6,356,759.769 | 298.25 | USA/DoD |
| Australian National (1966) | 6,378,160 | 6,356,774.719 | 298.25 | Australia |
| New International (1967) | 6,378,157.5 | 6,356,772.2 | 298.24961539 | |
| GRS-67 (1967) | 6,378,160 | 6,356,774.516 | 298.247167427 | |
| South American (1969) | 6,378,160 | 6,356,774.719 | 298.25 | South America |
| WGS-72 (1972) | 6,378,135 | 6,356,750.52 | 298.26 | USA/DoD |
| GRS-80 GRS 80 GRS 80, or Geodetic Reference System 1980, is a geodetic reference system consisting of a global reference ellipsoid and a gravity field model.-Geodesy:... (1979) |
6,378,137 | 6,356,752.3141 | 298.257222101 | Global ITRS International Terrestrial Reference System The International Terrestrial Reference System describes procedures for creating reference frames suitable for use with measurements on or near the Earth's surface. This is done in much the same way that a physical standard might be described as a set of procedures for creating a realization of... |
| WGS-84 (1984) | 6,378,137 | 6,356,752.3142 | 298.257223563 | Global GPS Global Positioning System The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites... |
| IERS IERS IERS may refer to:* International Earth Rotation and Reference Systems Service* Independent Electricity Retail Solutions Pty Ltd* Information Exchange Requirements - used within MODAF and DODAF as the OV-3 view - called Information Exchange Matrix.... (1989) |
6,378,136 | 6,356,751.302 | 298.257 | |
| IERS (2003) | 6,378,136.6 | 6,356,751.9 | 298.25642 |
More complicated figures
The possibility that the Earth's equator is an ellipse rather than a circle and therefore that the ellipsoid is triaxial has been a matter of scientific controversy for many years. Modern technological developments have furnished new and rapid methods for data collection and since the launch of Sputnik 1Sputnik 1
Sputnik 1 ) was the first artificial satellite to be put into Earth's orbit. It was launched into an elliptical low Earth orbit by the Soviet Union on 4 October 1957. The unanticipated announcement of Sputnik 1s success precipitated the Sputnik crisis in the United States and ignited the Space...
, orbital data have been used to investigate the theory of ellipticity.
A second theory, more complicated than triaxiality, proposed that observed long periodic orbital variations of the first Earth satellites indicate an additional depression at the south pole accompanied by a bulge of the same degree at the north pole. It is also contended that the northern middle latitudes were slightly flattened and the southern middle latitudes bulged in a similar amount. This concept suggested a slightly pear-shaped Earth and was the subject of much public discussion. Modern geodesy tends to retain the ellipsoid of revolution and treat triaxiality and pear shape as a part of the geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
figure: they are represented by the spherical harmonic coefficients
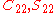 and
and 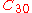 , respectively, corresponding to degree and order numbers 2.2 for the triaxiality and 3.0 for the pear shape.
, respectively, corresponding to degree and order numbers 2.2 for the triaxiality and 3.0 for the pear shape.Geoid
It was stated earlier that measurements are made on the apparent or topographic surface of the Earth and it has just been explained that computations are performed on an ellipsoid. One other surface is involved in geodetic measurement: the geoidGeoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
. In geodetic surveying, the computation of the geodetic coordinates of points is commonly performed on a reference ellipsoid
Reference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
closely approximating the size and shape of the Earth in the area of the survey. The actual measurements made on the surface of the Earth with certain instruments are however referred to the geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
. The ellipsoid is a mathematically defined regular surface with specific dimensions. The geoid, on the other hand, coincides with that surface to which the oceans would conform over the entire Earth if free to adjust to the combined effect of the Earth's mass attraction (gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
) and the centrifugal force of the Earth's rotation. As a result of the uneven distribution of the Earth's mass, the geoidal surface is irregular and, since the ellipsoid is a regular surface, the separations between the two, referred to as geoid undulations, geoid heights, or geoid separations, will be irregular as well.
The geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
is a surface along which the gravity potential is everywhere equal and to which the direction of gravity is always perpendicular (see equipotential surface
Equipotential surface
Equipotential surfaces are surfaces of constant scalar potential. They are used to visualize an -dimensional scalar potential function in dimensional space...
). The latter is particularly important because optical instruments containing gravity-reference leveling devices are commonly used to make geodetic measurements. When properly adjusted, the vertical axis of the instrument coincides with the direction of gravity and is, therefore, perpendicular to the geoid. The angle between the plumb line which is perpendicular to the geoid (sometimes called "the vertical") and the perpendicular to the ellipsoid (sometimes called "the ellipsoidal normal") is defined as the deflection of the vertical
Vertical deflection
The vertical deflection at a point on the earth is a measure of how far the direction of the local gravity field has been shifted by local anomalies such as nearby mountains....
. It has two components: an east-west and a north-south component.
Earth rotation and Earth's interior
Determining the exact figure of the Earth is not only a geodetic operation or a task of geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, but is also related to geophysics
Geophysics
Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
. Without any idea of the Earth's interior, we can state a "constant density" of 5.515 g/cm³ and, according to theoretical arguments (see Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, Albert Wangerin, etc.), such a body rotating like the Earth would have a flattening
Flattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
of 1:230.
In fact the measured flattening is 1:298.25, which is more similar to a sphere and a strong argument that the Earth's core
Inner core
The inner core of the Earth, its innermost hottest part as detected by seismological studies, is a primarily solid ball about in radius, or about 70% that of the Moon...
is very compact. Therefore the density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
must be a function of the depth, reaching from about 2.7 g/cm³ at the surface (rock density of granite
Granite
Granite is a common and widely occurring type of intrusive, felsic, igneous rock. Granite usually has a medium- to coarse-grained texture. Occasionally some individual crystals are larger than the groundmass, in which case the texture is known as porphyritic. A granitic rock with a porphyritic...
, limestone etc. – see regional geology
Geology
Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
) up to approximately 15 within the inner core. Modern seismology
Seismology
Seismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
yields a value of 16 g/cm³ at the center of the earth.
Global and regional gravity field
Also with implications for the physical exploration of the Earth's interior is the gravitational fieldGravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
, which can be measured very accurately at the surface and remotely by satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
s. True vertical
Vertical direction
In astronomy, geography, geometry and related sciences and contexts, a direction passing by a given point is said to be vertical if it is locally aligned with the gradient of the gravity field, i.e., with the direction of the gravitational force at that point...
generally does not correspond to theoretical vertical (deflection
Deflection (physics)
In physics deflection is the event where an object collides and bounces against a plane surface.In such collisions involving a sphere and a plane, the collision angle formed with the surface normal must equal the bounce angle , \alpha = \beta.Magnetic deflection refers to Lorentz forces acting...
ranges from 2" to 50") because topography
Topography
Topography is the study of Earth's surface shape and features or those ofplanets, moons, and asteroids...
and all geological masses disturb the gravitational field. Therefore the gross structure of the earth's crust and mantle can be determined by geodetic-geophysical models of the subsurface.
See also
- Clairaut's theoremClairaut's theoremClairaut's theorem, published in 1743 by Alexis Claude Clairaut in his Théorie de la figure de la terre, tirée des principes de l'hydrostatique, synthesized physical and geodetic evidence that the Earth is an oblate rotational ellipsoid. It is a general mathematical law applying to spheroids of...
- Geosciences, WGS84, EGM96EGM96EGM96 is a geopotential model of the Earth consisting of spherical harmonic coefficients complete to degree and order 360...
- Earth radiusEarth radiusBecause the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
, flatteningFlatteningThe flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
, meridian arcMeridian arcIn geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This... - reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
, geoid undulations - theoretical gravityTheoretical gravityIn geodesy and geophysics, theoretical gravity is a means to compare the true gravity on the Earth's surface with a physically smoothed model. The most common model of a smoothed Earth is the Earth ellipsoid....
, gravity formula - History: Flat EarthFlat EarthThe Flat Earth model is a belief that the Earth's shape is a plane or disk. Most ancient cultures have had conceptions of a flat Earth, including Greece until the classical period, the Bronze Age and Iron Age civilizations of the Near East until the Hellenistic period, India until the Gupta period ...
, EratosthenesEratosthenesEratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...
, Pierre BouguerPierre BouguerPierre Bouguer was a French mathematician, geophysicist, geodesist, and astronomer. He is also known as "the father of naval architecture"....
, Friedrich Robert HelmertFriedrich Robert HelmertFriedrich Robert Helmert was a German geodesist and an important writer on the theory of errors.Helmert was born in Freiberg, Kingdom of Saxony. After schooling in Freiberg and Dresden, he entered the Polytechnische Schule, now Technische Universität, in Dresden to study engineering science in 1859...

