
Geoid
Encyclopedia
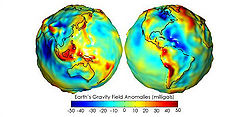
The geoid is that equipotential surface
which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest (relative to the rotating Earth), and extended through the continents (such as with very narrow canals). According to C.F. Gauss
, who first described it, it is the "mathematical figure of the Earth", a smooth but highly irregular surface that corresponds not to the actual surface of the Earth's crust, but to a surface which can only be known through extensive gravitational measurements and calculations. Despite being an important concept for almost two hundred years in the history of geodesy
and geophysics
, it has only been defined to high precision in recent decades, for instance by works of Petr Vaníček
and others. It is often described as the true physical figure of the Earth
, in contrast to the idealized geometrical figure of a reference ellipsoid
.
which is a mathematical idealized representation of the physical Earth, but considerably smoother than Earth's physical surface. Although the physical Earth has excursions of +8,000 m (Mount Everest
) and −11,000 m (Mariana Trench
), the geoid's total variation is less than 200 m (−106 to +85 m) compared to a perfect mathematical ellipsoid.
Sea level, if undisturbed by tides, currents and weather, would assume a surface equal to the geoid. If the continental land masses were criss-crossed by a series of tunnels or narrow canals, the sea level in these canals would also coincide with the geoid. In reality the geoid does not have a physical meaning under the continents, but geodesists are able to derive the heights of continental points above this imaginary, yet physically defined, surface by a technique called spirit leveling.
Being an equipotential surface
, the geoid is by definition a surface to which the force of gravity is everywhere perpendicular. This means that when travelling by ship, one does not notice the undulations of the geoid; the local vertical (plumb line
) is always perpendicular to the geoid and the local horizon tangential to it. Likewise, spirit levels will always be parallel to the geoid.
Note that a GPS receiver on a ship may, during the course of a long voyage, indicate height variations, even though the ship will always be at sea level (tides not considered). This is because GPS satellite
s, orbiting about the center of gravity of the Earth, can only measure heights relative to a geocentric reference ellipsoid. To obtain one's geoidal height, a raw GPS reading must be corrected. Conversely, height determined by spirit leveling from a tidal measurement station, as in traditional land surveying, will always be geoidal height.
Modern GPS receivers have a grid implemented inside where they obtain the geoid (e.g. EGM-96) height over the WGS ellipsoid from the current position. Then they are able to correct the height above WGS ellipsoid to the height above WGS84 geoid. In that case when the height is not zero on a ship it is because of the tides.
If that perfect sphere were then covered in water, the water would not be the same height everywhere. Instead, the water level would be higher or lower depending on the particular strength of gravity in that location.
s are often used to approximate the shape of the geoid. The current best such set of spherical harmonic coefficients is EGM96
(Earth Gravity Model 1996), determined in an international collaborative project led by NIMA
. The mathematical description of the non-rotating part of the potential function in this model is

 where
where  and
and  are geocentric (spherical) latitude and longitude respectively,
are geocentric (spherical) latitude and longitude respectively, 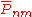 are the fully normalized associated Legendre polynomials
are the fully normalized associated Legendre polynomials
of degree and order
and order  , and
, and 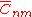 and
and  are the numerical coefficients of the model based on measured data. Note that the above equation describes the Earth's gravitational potential
are the numerical coefficients of the model based on measured data. Note that the above equation describes the Earth's gravitational potential
 , not the geoid itself, at location
, not the geoid itself, at location 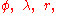 the co-ordinate
the co-ordinate  being the geocentric radius, i.e., distance from the Earth's centre. The geoid is a particular equipotential
being the geocentric radius, i.e., distance from the Earth's centre. The geoid is a particular equipotential
surface, and is somewhat involved to compute. The gradient of this potential also provides a model of the gravitational acceleration. EGM96 contains a full set of coefficients to degree and order 360 (i.e.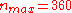 ) , describing details in the global geoid as small as 55 km (or 110 km, depending on your definition of resolution). The number of coefficients,
) , describing details in the global geoid as small as 55 km (or 110 km, depending on your definition of resolution). The number of coefficients, 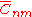 and
and  , can be determined by first observing in the equation for V that for a specific value of n there are two coefficients for every value of m except for m = 0. There is only one coefficient when m=0 since
, can be determined by first observing in the equation for V that for a specific value of n there are two coefficients for every value of m except for m = 0. There is only one coefficient when m=0 since 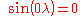 . There are thus (2n+1) coefficients for every value of n. Using these facts and the well known formula,
. There are thus (2n+1) coefficients for every value of n. Using these facts and the well known formula, 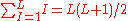 , it follows that the total number of coefficients is given by
, it follows that the total number of coefficients is given by
 using the EGM96 value of
using the EGM96 value of 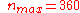 .
.
For many applications the complete series is unnecessarily complex and is truncated after a few (perhaps several dozen) terms.
New even higher resolution models are currently under development. For example, many of the authors of EGM96 are working on an updated model that should incorporate much of the new satellite gravity data (see, e.g., GRACE
), and should support up to degree and order 2160 (1/6 of a degree, requiring over 4 million coefficients).
NGA
has announced the availability of EGM2008, complete to spherical harmonic degree and order 2159, and contains additional coefficients extending to degree 2190 and order 2159. Software and data is on the Earth Gravitational Model 2008 (EGM2008) - WGS 84 Version page.
and co-workers improved on the Stokesian
approach to geoid computation. Their solution enables millimetre-to-centimetre accuracy in geoid computation
, an order-of-magnitude
improvement from previous classical solutions.
and
GRACE
, have enabled the study of time-variable geoid signals. The first products based on GOCE satellite data became available online in June, 2010, through the European Space Agency (ESA)’s Earth observation user services tools. ESA launched the satellite in March 2009 on a mission to map Earth's gravity with unprecedented accuracy and spatial resolution. On 31 March 2011, the new geoid was unveiled at the Fourth International GOCE User Workshop hosted at the Technische Universität München in Munich, Germany. Studies using the time-variable geoid computed from GRACE data have provided information on global hydrologic cycles, mass balances of ice sheet
s, and postglacial rebound. From postglacial rebound measurements, time-variable GRACE data can be used to deduce the viscosity
of Earth's mantle.
Equipotential surface
Equipotential surfaces are surfaces of constant scalar potential. They are used to visualize an -dimensional scalar potential function in dimensional space...
which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest (relative to the rotating Earth), and extended through the continents (such as with very narrow canals). According to C.F. Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, who first described it, it is the "mathematical figure of the Earth", a smooth but highly irregular surface that corresponds not to the actual surface of the Earth's crust, but to a surface which can only be known through extensive gravitational measurements and calculations. Despite being an important concept for almost two hundred years in the history of geodesy
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
and geophysics
Geophysics
Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
, it has only been defined to high precision in recent decades, for instance by works of Petr Vaníček
Petr Vanícek
Petr Vaníček is a Czech Canadian geodesist and theoretical geophysicist who has made important breakthroughs in theory of spectral analysis and geoid computation. He initiated the establishing of the Canadian Geophysical Union in 1974, and served as the Union's president between 1986 and 1988...
and others. It is often described as the true physical figure of the Earth
Figure of the Earth
The expression figure of the Earth has various meanings in geodesy according to the way it is used and the precision with which the Earth's size and shape is to be defined. The actual topographic surface is most apparent with its variety of land forms and water areas. This is, in fact, the surface...
, in contrast to the idealized geometrical figure of a reference ellipsoid
Reference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
.
Description
The geoid surface is irregular, unlike the reference ellipsoidReference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
which is a mathematical idealized representation of the physical Earth, but considerably smoother than Earth's physical surface. Although the physical Earth has excursions of +8,000 m (Mount Everest
Mount Everest
Mount Everest is the world's highest mountain, with a peak at above sea level. It is located in the Mahalangur section of the Himalayas. The international boundary runs across the precise summit point...
) and −11,000 m (Mariana Trench
Mariana Trench
The Mariana Trench or Marianas Trench is the deepest part of the world's oceans. It is located in the western Pacific Ocean, to the east of the Mariana Islands. The trench is about long but has a mean width of only...
), the geoid's total variation is less than 200 m (−106 to +85 m) compared to a perfect mathematical ellipsoid.
Sea level, if undisturbed by tides, currents and weather, would assume a surface equal to the geoid. If the continental land masses were criss-crossed by a series of tunnels or narrow canals, the sea level in these canals would also coincide with the geoid. In reality the geoid does not have a physical meaning under the continents, but geodesists are able to derive the heights of continental points above this imaginary, yet physically defined, surface by a technique called spirit leveling.
Being an equipotential surface
Equipotential surface
Equipotential surfaces are surfaces of constant scalar potential. They are used to visualize an -dimensional scalar potential function in dimensional space...
, the geoid is by definition a surface to which the force of gravity is everywhere perpendicular. This means that when travelling by ship, one does not notice the undulations of the geoid; the local vertical (plumb line
Plumb-bob
A plumb-bob or a plummet is a weight, usually with a pointed tip on the bottom, that is suspended from a string and used as a vertical reference line, or plumb-line....
) is always perpendicular to the geoid and the local horizon tangential to it. Likewise, spirit levels will always be parallel to the geoid.
Note that a GPS receiver on a ship may, during the course of a long voyage, indicate height variations, even though the ship will always be at sea level (tides not considered). This is because GPS satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
s, orbiting about the center of gravity of the Earth, can only measure heights relative to a geocentric reference ellipsoid. To obtain one's geoidal height, a raw GPS reading must be corrected. Conversely, height determined by spirit leveling from a tidal measurement station, as in traditional land surveying, will always be geoidal height.
Modern GPS receivers have a grid implemented inside where they obtain the geoid (e.g. EGM-96) height over the WGS ellipsoid from the current position. Then they are able to correct the height above WGS ellipsoid to the height above WGS84 geoid. In that case when the height is not zero on a ship it is because of the tides.
Simplified Example
The gravity field of the earth is neither perfect nor uniform. A flattened ellipsoid is typically used as the idealized earth, but even if the earth were perfectly spherical, the strength of gravity would not be the same everywhere, because density (and therefore mass) varies throughout the planet. This is due to magma distributions, mountain ranges, deep sea trenches, and so on.If that perfect sphere were then covered in water, the water would not be the same height everywhere. Instead, the water level would be higher or lower depending on the particular strength of gravity in that location.
Spherical harmonics representation
Spherical harmonicSpherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s are often used to approximate the shape of the geoid. The current best such set of spherical harmonic coefficients is EGM96
EGM96
EGM96 is a geopotential model of the Earth consisting of spherical harmonic coefficients complete to degree and order 360...
(Earth Gravity Model 1996), determined in an international collaborative project led by NIMA
National Geospatial-Intelligence Agency
The National Geospatial-Intelligence Agency is an agency of the federal government of the United States with the primary mission of collecting, analyzing and distributing geospatial intelligence in support of national security. NGA was formerly known as the National Imagery and Mapping Agency ...
. The mathematical description of the non-rotating part of the potential function in this model is


 and
and  are geocentric (spherical) latitude and longitude respectively,
are geocentric (spherical) latitude and longitude respectively, 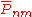 are the fully normalized associated Legendre polynomials
are the fully normalized associated Legendre polynomialsAssociated Legendre polynomials
In mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation\,y -2xy' + \left\,y = 0,\,or equivalently...
of degree
 and order
and order  , and
, and 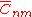 and
and  are the numerical coefficients of the model based on measured data. Note that the above equation describes the Earth's gravitational potential
are the numerical coefficients of the model based on measured data. Note that the above equation describes the Earth's gravitational potentialPotential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
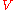 , not the geoid itself, at location
, not the geoid itself, at location 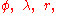 the co-ordinate
the co-ordinate  being the geocentric radius, i.e., distance from the Earth's centre. The geoid is a particular equipotential
being the geocentric radius, i.e., distance from the Earth's centre. The geoid is a particular equipotentialEquipotential
Equipotential or isopotential in mathematics and physics refers to a region in space where every point in it is at the same potential. This usually refers to a scalar potential , although it can also be applied to vector potentials...
surface, and is somewhat involved to compute. The gradient of this potential also provides a model of the gravitational acceleration. EGM96 contains a full set of coefficients to degree and order 360 (i.e.
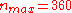 ) , describing details in the global geoid as small as 55 km (or 110 km, depending on your definition of resolution). The number of coefficients,
) , describing details in the global geoid as small as 55 km (or 110 km, depending on your definition of resolution). The number of coefficients, 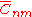 and
and  , can be determined by first observing in the equation for V that for a specific value of n there are two coefficients for every value of m except for m = 0. There is only one coefficient when m=0 since
, can be determined by first observing in the equation for V that for a specific value of n there are two coefficients for every value of m except for m = 0. There is only one coefficient when m=0 since 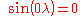 . There are thus (2n+1) coefficients for every value of n. Using these facts and the well known formula,
. There are thus (2n+1) coefficients for every value of n. Using these facts and the well known formula, 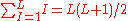 , it follows that the total number of coefficients is given by
, it follows that the total number of coefficients is given by using the EGM96 value of
using the EGM96 value of 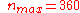 .
.For many applications the complete series is unnecessarily complex and is truncated after a few (perhaps several dozen) terms.
New even higher resolution models are currently under development. For example, many of the authors of EGM96 are working on an updated model that should incorporate much of the new satellite gravity data (see, e.g., GRACE
Gravity Recovery and Climate Experiment
The Gravity Recovery And Climate Experiment , a joint mission of NASA and the German Space Agency, has been making detailed measurements of Earth's gravity field since its launch in March 2002....
), and should support up to degree and order 2160 (1/6 of a degree, requiring over 4 million coefficients).
NGA
National Geospatial-Intelligence Agency
The National Geospatial-Intelligence Agency is an agency of the federal government of the United States with the primary mission of collecting, analyzing and distributing geospatial intelligence in support of national security. NGA was formerly known as the National Imagery and Mapping Agency ...
has announced the availability of EGM2008, complete to spherical harmonic degree and order 2159, and contains additional coefficients extending to degree 2190 and order 2159. Software and data is on the Earth Gravitational Model 2008 (EGM2008) - WGS 84 Version page.
Precise geoid
The 1990s saw important discoveries in theory of geoid computation. The Precise Geoid Solution by VaníčekPetr Vanícek
Petr Vaníček is a Czech Canadian geodesist and theoretical geophysicist who has made important breakthroughs in theory of spectral analysis and geoid computation. He initiated the establishing of the Canadian Geophysical Union in 1974, and served as the Union's president between 1986 and 1988...
and co-workers improved on the Stokesian
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
approach to geoid computation. Their solution enables millimetre-to-centimetre accuracy in geoid computation
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
, an order-of-magnitude
Order of magnitude
An order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
improvement from previous classical solutions.
Time-variability
Recent satellite missions, such as GOCEGravity Field and Steady-State Ocean Circulation Explorer
The Gravity Field and Steady-State Ocean Circulation Explorer is an ESA satellite that was launched on March 17, 2009. It is a satellite carrying a highly sensitive gravity gradiometer which detects fine density differences in the crust and oceans of the Earth.GOCE data will have many uses,...
and
GRACE
Gravity Recovery and Climate Experiment
The Gravity Recovery And Climate Experiment , a joint mission of NASA and the German Space Agency, has been making detailed measurements of Earth's gravity field since its launch in March 2002....
, have enabled the study of time-variable geoid signals. The first products based on GOCE satellite data became available online in June, 2010, through the European Space Agency (ESA)’s Earth observation user services tools. ESA launched the satellite in March 2009 on a mission to map Earth's gravity with unprecedented accuracy and spatial resolution. On 31 March 2011, the new geoid was unveiled at the Fourth International GOCE User Workshop hosted at the Technische Universität München in Munich, Germany. Studies using the time-variable geoid computed from GRACE data have provided information on global hydrologic cycles, mass balances of ice sheet
Ice sheet
An ice sheet is a mass of glacier ice that covers surrounding terrain and is greater than 50,000 km² , thus also known as continental glacier...
s, and postglacial rebound. From postglacial rebound measurements, time-variable GRACE data can be used to deduce the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
of Earth's mantle.
External links
- Main NGA (was NIMA) page on Earth gravity models
- EGM96 NASA GSFC Earth gravity model
- Earth Gravitational Model 2008 (EGM2008, Released in July 2008)
- NOAA Geoid webpage
- GeographicLib provides a utility GeoidEval (with source code) to evaluate the geoid height for the EGM84, EGM96EGM96EGM96 is a geopotential model of the Earth consisting of spherical harmonic coefficients complete to degree and order 360...
, and EGM2008 earth gravity models. Here is an online version of GeoidEval. - Kiamehr's Geoid Home Page
- Geoid tutorial from Li and Gotze (964KB pdf file)
- Geoid tutorial at GRACE website
- Precise Geoid Determination Based on the Least-Squares Modification of Stokes’ Formula(PhD Thesis PDF)

