Discrete sine transform
Encyclopedia
In mathematics
, the discrete sine transform (DST) is a Fourier-related transform similar to the discrete Fourier transform
(DFT), but using a purely real
matrix
. It is equivalent to the imaginary parts of a DFT of roughly twice the length, operating on real data with odd
symmetry
(since the Fourier transform of a real and odd function is imaginary and odd), where in some variants the input and/or output data are shifted by half a sample.
A related transform is the discrete cosine transform
(DCT), which is equivalent to a DFT of real and even functions. See the DCT article for a general discussion of how the boundary conditions relate the various DCT and DST types.
s by spectral methods, where the different variants of the DST correspond to slightly different odd/even boundary conditions at the two ends of the array.
with different frequencies and amplitude
s. Like the discrete Fourier transform
(DFT), a DST operates on a function at a finite number of discrete data points. The obvious distinction between a DST and a DFT is that the former uses only sine functions, while the latter uses both cosines and sines (in the form of complex exponentials). However, this visible difference is merely a consequence of a deeper distinction: a DST implies different boundary conditions than the DFT or other related transforms.
The Fourier-related transforms that operate on a function over a finite domain
, such as the DFT or DST or a Fourier series
, can be thought of as implicitly defining an extension of that function outside the domain. That is, once you write a function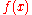
as a sum of sinusoids, you can evaluate that sum at any 
, even for 
where the original 
was not specified. The DFT, like the Fourier series, implies a periodic
extension of the original function. A DST, like a sine transform
, implies an odd
extension of the original function.
However, because DSTs operate on finite, discrete sequences, two issues arise that do not apply for the continuous sine transform. First, one has to specify whether the function is even or odd at both the left and right boundaries of the domain (i.e. the min-n and max-n boundaries in the definitions below, respectively). Second, one has to specify around what point the function is even or odd. In particular, consider a sequence (a,b,c) of three equally spaced data points, and say that we specify an odd left boundary. There are two sensible possibilities: either the data is odd about the point prior to a, in which case the odd extension is (−c,−b,−a,0,a,b,c), or the data is odd about the point halfway between a and the previous point, in which case the odd extension is (−c,−b,−a,a,b,c)
These choices lead to all the standard variations of DSTs and also discrete cosine transform
s (DCTs).
Each boundary can be either even or odd (2 choices per boundary) and can be symmetric about a data point or the point halfway between two data points (2 choices per boundary), for a total of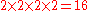
possibilities. Half of these possibilities, those where the left boundary is odd, correspond to the 8 types of DST; the other half are the 8 types of DCT.
These different boundary conditions strongly affect the applications of the transform, and lead to uniquely useful properties for the various DCT types. Most directly, when using Fourier-related transforms to solve partial differential equation
s by spectral method
s, the boundary conditions are directly specified as a part of the problem being solved.
, invertible function
F : RN -> RN (where R denotes the set of real number
s), or equivalently an N × N square matrix. There are several variants of the DST with slightly modified definitions. The N real numbers x0, ...., xN-1 are transformed into the N real numbers X0, ..., XN-1 according to one of the formulas:
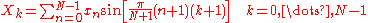
The DST-I matrix is orthogonal
(up to a scale factor).
A DST-I is exactly equivalent to a DFT of a real sequence that is odd around the zero-th and middle points, scaled by 1/2. For example, a DST-I of N=3 real numbers (a,b,c) is exactly equivalent to a DFT of eight real numbers (0,a,b,c,0,−c,−b,−a) (odd symmetry), scaled by 1/2. (In contrast, DST types II-IV involve a half-sample shift in the equivalent DFT.) This is the reason for the N+1 in the denominator of the sine function: the equivalent DFT has 2(N+1) points and has 2π/2(N+1) in its sinusoid frequency, so the DST-I has π/(N+1) in its frequency.
Thus, the DST-I corresponds to the boundary conditions: xn is odd around n=-1 and odd around n=N; similarly for Xk.
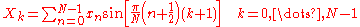
Some authors further multiply the XN-1 term by 1/√2 (see below for the corresponding change in DST-III). This makes the DST-II matrix orthogonal
(up to a scale factor), but breaks the direct correspondence with a real-odd DFT of half-shifted input.
The DST-II implies the boundary conditions: xn is odd around n=-1/2 and odd around n=N-1/2; Xk is odd around k=-1 and even around k=N-1.
Some authors further multiply the xN-1 term by √2 (see above for the corresponding change in DST-II). This makes the DST-III matrix orthogonal
(up to a scale factor), but breaks the direct correspondence with a real-odd DFT of half-shifted output.
The DST-III implies the boundary conditions: xn is odd around n=-1 and even around n=N-1; Xk is odd around k=-1/2 and odd around k=N-1/2.
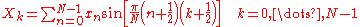
The DST-IV matrix is orthogonal
(up to a scale factor).
The DST-IV implies the boundary conditions: xn is odd around n=-1/2 and even around n=N-1/2; similarly for Xk.
Like for the DFT
, the normalization factor in front of these transform definitions is merely a convention and differs between treatments. For example, some authors multiply the transforms by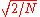
so that the inverse does not require any additional multiplicative factor.
(FFT). (One can also compute DSTs via FFTs combined with O(N) pre- and post-processing steps.)
A DST-II or DST-IV can be computed from a DCT-II or DCT-IV (see discrete cosine transform
), respectively, by reversing the order of the inputs and flipping the sign of every other output, and vice versa for DST-III from DCT-III. In this way it follows that types II–IV of the DST require exactly the same number of arithmetic operations (additions and multiplications) as the corresponding DCT types.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the discrete sine transform (DST) is a Fourier-related transform similar to the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT), but using a purely real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. It is equivalent to the imaginary parts of a DFT of roughly twice the length, operating on real data with odd
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
(since the Fourier transform of a real and odd function is imaginary and odd), where in some variants the input and/or output data are shifted by half a sample.
A related transform is the discrete cosine transform
Discrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
(DCT), which is equivalent to a DFT of real and even functions. See the DCT article for a general discussion of how the boundary conditions relate the various DCT and DST types.
Applications
DSTs are widely employed in solving partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s by spectral methods, where the different variants of the DST correspond to slightly different odd/even boundary conditions at the two ends of the array.
Informal overview
Like any Fourier-related transform, discrete sine transforms (DSTs) express a function or a signal in terms of a sum of sinusoidsTrigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
with different frequencies and amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
s. Like the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT), a DST operates on a function at a finite number of discrete data points. The obvious distinction between a DST and a DFT is that the former uses only sine functions, while the latter uses both cosines and sines (in the form of complex exponentials). However, this visible difference is merely a consequence of a deeper distinction: a DST implies different boundary conditions than the DFT or other related transforms.
The Fourier-related transforms that operate on a function over a finite domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
, such as the DFT or DST or a Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, can be thought of as implicitly defining an extension of that function outside the domain. That is, once you write a function
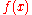as a sum of sinusoids, you can evaluate that sum at any , even for where the original was not specified. The DFT, like the Fourier series, implies a periodicPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
extension of the original function. A DST, like a sine transform
Sine and cosine transforms
In mathematics, the Fourier sine and cosine transforms are special cases of thecontinuous Fourier transform, arising naturally when attempting to transform odd and even functions, respectively.The general Fourier transform is defined as:...
, implies an odd
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
extension of the original function.
However, because DSTs operate on finite, discrete sequences, two issues arise that do not apply for the continuous sine transform. First, one has to specify whether the function is even or odd at both the left and right boundaries of the domain (i.e. the min-n and max-n boundaries in the definitions below, respectively). Second, one has to specify around what point the function is even or odd. In particular, consider a sequence (a,b,c) of three equally spaced data points, and say that we specify an odd left boundary. There are two sensible possibilities: either the data is odd about the point prior to a, in which case the odd extension is (−c,−b,−a,0,a,b,c), or the data is odd about the point halfway between a and the previous point, in which case the odd extension is (−c,−b,−a,a,b,c)
These choices lead to all the standard variations of DSTs and also discrete cosine transform
Discrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
s (DCTs).
Each boundary can be either even or odd (2 choices per boundary) and can be symmetric about a data point or the point halfway between two data points (2 choices per boundary), for a total of
possibilities. Half of these possibilities, those where the left boundary is odd, correspond to the 8 types of DST; the other half are the 8 types of DCT.These different boundary conditions strongly affect the applications of the transform, and lead to uniquely useful properties for the various DCT types. Most directly, when using Fourier-related transforms to solve partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s by spectral method
Spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
s, the boundary conditions are directly specified as a part of the problem being solved.
Definition
Formally, the discrete sine transform is a linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, invertible function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
F : RN -> RN (where R denotes the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s), or equivalently an N × N square matrix. There are several variants of the DST with slightly modified definitions. The N real numbers x0, ...., xN-1 are transformed into the N real numbers X0, ..., XN-1 according to one of the formulas:
DST-I
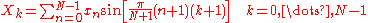
The DST-I matrix is orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(up to a scale factor).
A DST-I is exactly equivalent to a DFT of a real sequence that is odd around the zero-th and middle points, scaled by 1/2. For example, a DST-I of N=3 real numbers (a,b,c) is exactly equivalent to a DFT of eight real numbers (0,a,b,c,0,−c,−b,−a) (odd symmetry), scaled by 1/2. (In contrast, DST types II-IV involve a half-sample shift in the equivalent DFT.) This is the reason for the N+1 in the denominator of the sine function: the equivalent DFT has 2(N+1) points and has 2π/2(N+1) in its sinusoid frequency, so the DST-I has π/(N+1) in its frequency.
Thus, the DST-I corresponds to the boundary conditions: xn is odd around n=-1 and odd around n=N; similarly for Xk.
DST-II
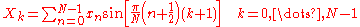
Some authors further multiply the XN-1 term by 1/√2 (see below for the corresponding change in DST-III). This makes the DST-II matrix orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(up to a scale factor), but breaks the direct correspondence with a real-odd DFT of half-shifted input.
The DST-II implies the boundary conditions: xn is odd around n=-1/2 and odd around n=N-1/2; Xk is odd around k=-1 and even around k=N-1.
DST-III
Some authors further multiply the xN-1 term by √2 (see above for the corresponding change in DST-II). This makes the DST-III matrix orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(up to a scale factor), but breaks the direct correspondence with a real-odd DFT of half-shifted output.
The DST-III implies the boundary conditions: xn is odd around n=-1 and even around n=N-1; Xk is odd around k=-1/2 and odd around k=N-1/2.
DST-IV
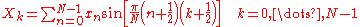
The DST-IV matrix is orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(up to a scale factor).
The DST-IV implies the boundary conditions: xn is odd around n=-1/2 and even around n=N-1/2; similarly for Xk.
DST V-VIII
DST types I-IV are equivalent to real-odd DFTs of even order. In principle, there are actually four additional types of discrete sine transform (Martucci, 1994), corresponding to real-odd DFTs of logically odd order, which have factors of N+1/2 in the denominators of the sine arguments. However, these variants seem to be rarely used in practice.Inverse transforms
The inverse of DST-I is DST-I multiplied by 2/(N+1). The inverse of DST-IV is DST-IV multiplied by 2/N. The inverse of DST-II is DST-III multiplied by 2/N (and vice versa).Like for the DFT
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, the normalization factor in front of these transform definitions is merely a convention and differs between treatments. For example, some authors multiply the transforms by
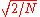so that the inverse does not require any additional multiplicative factor.Computation
Although the direct application of these formulas would require O(N2) operations, it is possible to compute the same thing with only O(N log N) complexity by factorizing the computation similar to the fast Fourier transformFast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT). (One can also compute DSTs via FFTs combined with O(N) pre- and post-processing steps.)
A DST-II or DST-IV can be computed from a DCT-II or DCT-IV (see discrete cosine transform
Discrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
), respectively, by reversing the order of the inputs and flipping the sign of every other output, and vice versa for DST-III from DCT-III. In this way it follows that types II–IV of the DST require exactly the same number of arithmetic operations (additions and multiplications) as the corresponding DCT types.