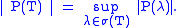Decomposition of spectrum (functional analysis)
Encyclopedia
In mathematics
, especially functional analysis
, the spectrum
of an operator generalizes the notion of eigenvalues. Given an operator, it is sometimes useful to break up the spectrum into various parts. This article discusses a few examples of such decompositions.
, L(X) the family of bounded operator
s on X.
A complex number λ is in the spectrum of T, denoted σ(T), if T − λ does not have bounded inverse. If T − λ is invertible (i.e., if it is one-to-one and onto), then its inverse is bounded; this follows directly from the open mapping theorem
. So, λ is in the spectrum of T if and only if T − λ is either not one-to-one or not onto. One can easily check that if T − λ is one-to-one, bounded below (i.e. does not send far apart elements of X too close together), and has dense range, then in fact T − λ must be onto, so λ will not be in σ(T). Therefore, if λ is in σ(T), one of the following must be true:
Correspondingly, for T ∈ L(X), its spectrum σ(T) can be classified as follows:
So σ(T) is the disjoint union
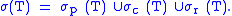
If X* is the dual space of X, and T* : X* → X* is the adjoint operator of T, then
σ(T) = σ(T*).
Theorem For a bounded operator T, σr(T) ⊂ σp(T*)* ⊂ σr(T) ∪ σp(T).
Proof
The notation <·, φ> will denote an element of X*, i.e. x → <x, φ> is the action of a bounded linear functional φ. Let λ ∈ σr(T). So Ran(T - λ) is not dense in X. By the Hahn–Banach theorem
, there exists a non-zero φ ∈ X* that vanishes on Ran(T - λ). For all x ∈ X,
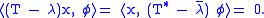
Therefore (T* − \overline{λ})φ = 0 ∈ X* and \overline{λ} is an eigenvalue of T*. The shows the first part of the inclusion. Next suppose that (T* − \overline{λ})φ = 0 where φ ≠ 0, i.e.
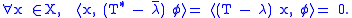
If Ran(T − λ) is dense, then φ must be the zero functional, a contradiction. The claim is proved.
In particular, when X is a reflexive Banach space, σr(T*) ⊂ σp(T**) = σp(T).
. A function h: S → C is called essentially bounded if h is bounded μ-almost everywhere. An essentially bounded h induces a bounded multiplication operator Th on Lp(μ):
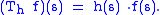
The operator norm of T is the essential supremum of h. The essential range of h is defined in the following way: a complex number λ is in the essential range of T if for all ε > 0, the preimage of the open ball Bε(λ) under h has strictly positive measure. We will show first that σ(Th) coincides with the essential range of h and then examine its various parts.
If λ is not in the essential range of h, take ε > 0 such that h−1(Bε(λ)) has zero measure. The function g(s) = 1/(h(s) − λ) is bounded almost everywhere by 1/ε. The multiplication operator Tg satisfies
Tg · Th − λ = Th − λ · Tg = I. So λ does not lie in spectrum of Th. On the other hand, if λ lies in the essential range of h, consider the sequence of sets {Sn =
h-1(B1/n(λ))}. Each Sn has positive measure. Let fn be the characteristic function of Sn. We can compute directly
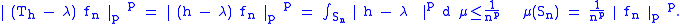
This shows Th − λ is not bounded below, therefore not invertible.
If λ is such that μ( h−1({λ})) > 0, then λ lies in the point spectrum of Th: Pick an open ball Bε(λ) that contains only λ from the essential range. Let f be the characteristic function of h−1(Bε(λ)), then
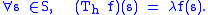
Any λ in the essential range of h that does not have a positive measure preimage is in the continuous spectrum or in the resolvent spectrum of Th. To show this is to show that Th − λ has dense range for all such λ. Given f ∈ Lp(μ), again we consider the sequence of sets {Sn = h−1(B1/n(λ))}. Let gn be the characteristic function of S − Sn. Define
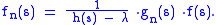
Direct calculation shows that fn ∈ Lp(μ), and, by the dominated convergence theorem
,
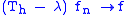
in the Lp(μ) norm.
Therefore multiplication operators have no residual spectrum. In particular, by the spectral theorem
, normal operator
s on a Hilbert space have no residual spectrum.
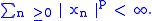
For 1 < p < ∞, l p is reflexive. Define the left shift T : l p → l p by
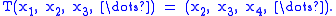
T is a partial isometry
with operator norm 1. So σ(T) lies in the closed unit disk of the complex plane.
T* is the right shift (or unilateral shift), which is an isometry, on l q where 1/p + 1/q = 1:
For λ ∈ C with |λ| < 1,
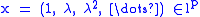
and T x = λ x. Consequently the point spectrum of T contains open unit disk. Invoking reflexivity and the theorem given above, we can deduce that the open unit disk lies in the residual spectrum of T*.
The spectrum of a bounded operator is closed, which implies the unit circle, { |λ| = 1 } ⊂ C, is in σ(T). Also, T* has no eigenvalues, i.e. σp(T*) is empty. Again by reflexivity of l p and the theorem given above, we have that σr(T)
is also empty. Therefore, for a complex number λ with unit norm, one must have λ ∈ σp(T) or λ ∈ σc(T). Now if |λ| = 1 and
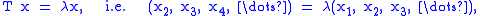
then
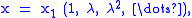
which can not be in l p, a contradiction. This means the unit circle must be the continuous spectrum of T.
For the right shift T*, σr(T*) is the open unit disk and σc(T*) is the unit circle.
For p = 1, one can perform a similar analysis. The results will not be exactly the same, since reflexivity no longer holds.
s are Banach spaces, so the above discussion applies to bounded operators on Hilbert spaces as well, although possible differences may arise from the adjoint operation on operators. For example, let H be a Hilbert space and T ∈ L(H), σ(T*) is not σ(T) but rather its image under complex conjugation.
For a self adjoint T ∈ L(H), the Borel functional calculus
gives additional ways to break up the spectrum naturally.
. For the continuous functional calculus, the key ingredients are the following:
The family C(σ(T)) is a Banach algebra
when endowed with the uniform norm. So the mapping
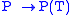
is an isometric homomorphism from a dense subset of C(σ(T)) to L(H). Extending the mapping by continuity gives f(T) for f ∈ C(σ(T)): let Pn be polynomials such that Pn → f uniformly and define f(T) = lim Pn(T). This is the continuous functional calculus.
For a fixed h ∈ H, we notice that
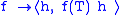
is a positive linear functional on C(σ(T)). According to the Riesz-Markov representation theorem that there exists a unique measure μh on σ(T) such that
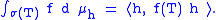
This measure is sometimes called the spectral measure associated to h. The spectral measures can be used to extend the continuous functional calculus to bounded Borel functions. For a bounded function g that is Borel measurable, define, for a proposed g(T)
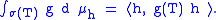
Via the polarization identity
, one can recover (since H is assumed to be complex)
and therefore g(T) h for arbitrary h.
In the present context, the spectral measures, combined with a result from measure theory, give a decomposition of σ(T).
, μh can be decomposed into three mutually singular parts:
where μac is absolutely continuous with respect to the Lebesgue measure, and μsc is singular with respect to the Lebesgue measure,
and μpp is a pure point measure.
All three types of measures are invariant under linear operations. Let Hac be the subspace consisting of vectors whose spectral measures are absolutely continuous with respect to the Lebesgue measure
. Define Hpp and Hsc in analogous fashion. These subspaces are invariant under T. For example, if h ∈ Hac and k = T h. Let χ be the characteristic function of some Borel set in σ(T), then
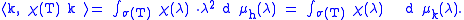
So
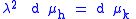
and k ∈ Hac. Furthermore, applying the spectral theorem gives
This leads to the following definitions:
The closure of the eigenvalues is the spectrum of T restricted to Hpp. So
Unlike the Banach space formulation, the union
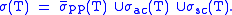
need not be disjoint. It is disjoint when the operator T is of uniform multiplicity, say m, i.e. if T is unitarily equivalent to multiplication by λ on the direct sum
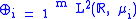
for some Borel measures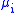
. When more than one measure appears in the above expression, we see that it is possible for the union of the three types of spectra to not be disjoint. If λ ∈ σac(T) ∩ σpp(T), λ is sometimes called an eigenvalue embedded in the absolutely continuous spectrum.
When T is unitarily equivalent to multiplication by λ on
the decomposition of σ(T) from Borel functional calculus is a refinement of the Banach space case.
s.
In quantum mechanics
, observables are, not necessarily bounded, self adjoint operators and their spectra are the possible outcomes of measurements. Absolutely continuous spectrum of a physical observable corresponds to free state
s of a system, while the pure point spectrum corresponds to bound state
s. The singular spectrum correspond to physically impossible outcomes. An example of a quantum mechanical observable which has purely continuous spectrum is the position operator
of a free particle moving on a line. Its spectrum is the entire real line. Also, since the momentum operator
is unitarily equivalent to the position operator, via the Fourier transform
, they have the same spectrum.
Intuition may induce one to say that the discreteness of the spectrum is intimately related to the corresponding states being "localized". However, a careful mathematical analysis shows that this is not true. The following
is an element of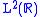
and increasing as 
.
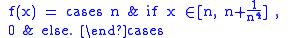
However, the phenomena of Anderson localization
and dynamical localization describe, when the eigenfunctions are localized in a physical sense. Anderson Localization means that eigenfunctions decay exponentially as
. Dynamical localization is more subtle to define.
Sometimes, when performing physical quantum mechanical calculations, one encounters "eigenvectors" that do not lie in L2(R), i.e. wave functions that are not localized. These are the free states of the system. As stated above, in the mathematical formulation, the free states correspond to the absolutely continuous spectrum. Alternatively, if it is insisted that the notion of eigenvectors and eigenvalues survive the passage to the rigorous, one can consider operators on rigged Hilbert space
s.
It was believed for some time that singular spectrum is something artificial. However, examples as the almost Mathieu operator and random Schrödinger operators have shown, that all types of spectra arise naturally in physics.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of an operator generalizes the notion of eigenvalues. Given an operator, it is sometimes useful to break up the spectrum into various parts. This article discusses a few examples of such decompositions.
Operators on Banach space
Let X be a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, L(X) the family of bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s on X.
A complex number λ is in the spectrum of T, denoted σ(T), if T − λ does not have bounded inverse. If T − λ is invertible (i.e., if it is one-to-one and onto), then its inverse is bounded; this follows directly from the open mapping theorem
Open mapping theorem (functional analysis)
In functional analysis, the open mapping theorem, also known as the Banach–Schauder theorem , is a fundamental result which states that if a continuous linear operator between Banach spaces is surjective then it is an open map...
. So, λ is in the spectrum of T if and only if T − λ is either not one-to-one or not onto. One can easily check that if T − λ is one-to-one, bounded below (i.e. does not send far apart elements of X too close together), and has dense range, then in fact T − λ must be onto, so λ will not be in σ(T). Therefore, if λ is in σ(T), one of the following must be true:
- T − λ is not injective.
- T − λ is injective, and has denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
. But T − λ is not bounded below, and we fail to get that the range is all of X. Equivalently, the densely-defined linear map (T − λ) x → x is not bounded, therefore can not be extended to all of X. - T − λ is injective and does not have dense range. In this case, the map (T − λ) x → x may be bounded or unbounded, but in any case does not admit a unique extension to a bounded linear map on all of X.
Correspondingly, for T ∈ L(X), its spectrum σ(T) can be classified as follows:
- The point spectrum of T consists of eigenvalues of T and will be denoted by σp(T). λ ∈ σ(T) is in the point spectrum if and only if T − λ is not injective.
- If λ ∈ σ(T) is not an eigenvalue and the range of T − λ, Ran(T − λ), is dense in X, λ is said to be in the continuous spectrum, σc(T), of T.
- If T − λ is injective and Ran(T − λ) is not dense, λ is in the residual spectrum of T, σr(T).
So σ(T) is the disjoint union
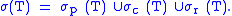
If X* is the dual space of X, and T* : X* → X* is the adjoint operator of T, then
σ(T) = σ(T*).
Theorem For a bounded operator T, σr(T) ⊂ σp(T*)* ⊂ σr(T) ∪ σp(T).
Proof
The notation <·, φ> will denote an element of X*, i.e. x → <x, φ> is the action of a bounded linear functional φ. Let λ ∈ σr(T). So Ran(T - λ) is not dense in X. By the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
, there exists a non-zero φ ∈ X* that vanishes on Ran(T - λ). For all x ∈ X,
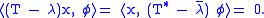
Therefore (T* − \overline{λ})φ = 0 ∈ X* and \overline{λ} is an eigenvalue of T*. The shows the first part of the inclusion. Next suppose that (T* − \overline{λ})φ = 0 where φ ≠ 0, i.e.
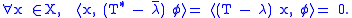
If Ran(T − λ) is dense, then φ must be the zero functional, a contradiction. The claim is proved.
In particular, when X is a reflexive Banach space, σr(T*) ⊂ σp(T**) = σp(T).
Multiplication operator
Given a σ-finite measure space (S, Σ, μ), consider the Banach space Lp(μ)Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. A function h: S → C is called essentially bounded if h is bounded μ-almost everywhere. An essentially bounded h induces a bounded multiplication operator Th on Lp(μ):
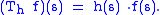
The operator norm of T is the essential supremum of h. The essential range of h is defined in the following way: a complex number λ is in the essential range of T if for all ε > 0, the preimage of the open ball Bε(λ) under h has strictly positive measure. We will show first that σ(Th) coincides with the essential range of h and then examine its various parts.
If λ is not in the essential range of h, take ε > 0 such that h−1(Bε(λ)) has zero measure. The function g(s) = 1/(h(s) − λ) is bounded almost everywhere by 1/ε. The multiplication operator Tg satisfies
Tg · Th − λ = Th − λ · Tg = I. So λ does not lie in spectrum of Th. On the other hand, if λ lies in the essential range of h, consider the sequence of sets {Sn =
h-1(B1/n(λ))}. Each Sn has positive measure. Let fn be the characteristic function of Sn. We can compute directly
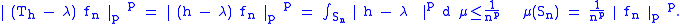
This shows Th − λ is not bounded below, therefore not invertible.
If λ is such that μ( h−1({λ})) > 0, then λ lies in the point spectrum of Th: Pick an open ball Bε(λ) that contains only λ from the essential range. Let f be the characteristic function of h−1(Bε(λ)), then
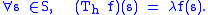
Any λ in the essential range of h that does not have a positive measure preimage is in the continuous spectrum or in the resolvent spectrum of Th. To show this is to show that Th − λ has dense range for all such λ. Given f ∈ Lp(μ), again we consider the sequence of sets {Sn = h−1(B1/n(λ))}. Let gn be the characteristic function of S − Sn. Define
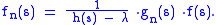
Direct calculation shows that fn ∈ Lp(μ), and, by the dominated convergence theorem
Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
,
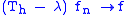
in the Lp(μ) norm.
Therefore multiplication operators have no residual spectrum. In particular, by the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
s on a Hilbert space have no residual spectrum.
Shifts
In the special case when S is the set of natural numbers and μ is the counting measure. The corresponding Lp(μ) is denoted by lp. This space consists of complex valued sequences {xn} such that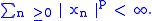For 1 < p < ∞, l p is reflexive. Define the left shift T : l p → l p by
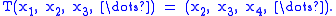
T is a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
with operator norm 1. So σ(T) lies in the closed unit disk of the complex plane.
T* is the right shift (or unilateral shift), which is an isometry, on l q where 1/p + 1/q = 1:
For λ ∈ C with |λ| < 1,
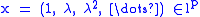
and T x = λ x. Consequently the point spectrum of T contains open unit disk. Invoking reflexivity and the theorem given above, we can deduce that the open unit disk lies in the residual spectrum of T*.
The spectrum of a bounded operator is closed, which implies the unit circle, { |λ| = 1 } ⊂ C, is in σ(T). Also, T* has no eigenvalues, i.e. σp(T*) is empty. Again by reflexivity of l p and the theorem given above, we have that σr(T)
is also empty. Therefore, for a complex number λ with unit norm, one must have λ ∈ σp(T) or λ ∈ σc(T). Now if |λ| = 1 and
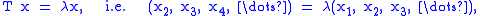
then
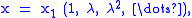
which can not be in l p, a contradiction. This means the unit circle must be the continuous spectrum of T.
For the right shift T*, σr(T*) is the open unit disk and σc(T*) is the unit circle.
For p = 1, one can perform a similar analysis. The results will not be exactly the same, since reflexivity no longer holds.
Unbounded operators
The spectrum of an unbounded operator can be divided into three parts in exactly the same way as in the bounded case.Self adjoint operators on Hilbert space
Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s are Banach spaces, so the above discussion applies to bounded operators on Hilbert spaces as well, although possible differences may arise from the adjoint operation on operators. For example, let H be a Hilbert space and T ∈ L(H), σ(T*) is not σ(T) but rather its image under complex conjugation.
For a self adjoint T ∈ L(H), the Borel functional calculus
Borel functional calculus
In functional analysis, a branch of mathematics, the Borel functional calculus is a functional calculus , which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2...
gives additional ways to break up the spectrum naturally.
Borel functional calculus
This subsection briefly sketches the development of this calculus. The idea is to first establish the continuous functional calculus then pass to measurable functions via the Riesz-Markov representation theoremRiesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
. For the continuous functional calculus, the key ingredients are the following:
- 1. If T is self adjoint, then for any polynomial P, the operator norm
-
- 2. The Stone-Weierstrass theoremStone-Weierstrass theoremIn mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function...
, which gives that the family of polynomials (with complex coefficients), is dense in C(σ(T)), the continuous functions on σ(T).
The family C(σ(T)) is a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
when endowed with the uniform norm. So the mapping
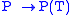
is an isometric homomorphism from a dense subset of C(σ(T)) to L(H). Extending the mapping by continuity gives f(T) for f ∈ C(σ(T)): let Pn be polynomials such that Pn → f uniformly and define f(T) = lim Pn(T). This is the continuous functional calculus.
For a fixed h ∈ H, we notice that
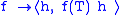
is a positive linear functional on C(σ(T)). According to the Riesz-Markov representation theorem that there exists a unique measure μh on σ(T) such that
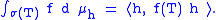
This measure is sometimes called the spectral measure associated to h. The spectral measures can be used to extend the continuous functional calculus to bounded Borel functions. For a bounded function g that is Borel measurable, define, for a proposed g(T)
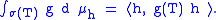
Via the polarization identity
Polarization identity
In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...
, one can recover (since H is assumed to be complex)
and therefore g(T) h for arbitrary h.
In the present context, the spectral measures, combined with a result from measure theory, give a decomposition of σ(T).
Decomposing the spectrum
Let h ∈ H and μh be its corresponding spectral measure on σ(T) ⊂ R. According to a refinement of Lebesgue's decomposition theoremLebesgue's decomposition theorem
In mathematics, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem which states that given \mu and \nu two σ-finite signed measures on a measurable space , there exist two σ-finite signed measures \nu_0 and \nu_1 such that:* \nu=\nu_0+\nu_1\, * \nu_0\ll\mu *...
, μh can be decomposed into three mutually singular parts:
where μac is absolutely continuous with respect to the Lebesgue measure, and μsc is singular with respect to the Lebesgue measure,
and μpp is a pure point measure.
All three types of measures are invariant under linear operations. Let Hac be the subspace consisting of vectors whose spectral measures are absolutely continuous with respect to the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. Define Hpp and Hsc in analogous fashion. These subspaces are invariant under T. For example, if h ∈ Hac and k = T h. Let χ be the characteristic function of some Borel set in σ(T), then
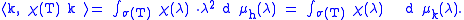
So
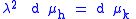
and k ∈ Hac. Furthermore, applying the spectral theorem gives
This leads to the following definitions:
- The spectrum of T restricted to Hac is called the absolutely continuous spectrum of T, σac(T).
- The spectrum of T restricted to Hsc is called its singular spectrum, σsc(T).
- The set of eigenvalues of T are called the pure point spectrum of T, σpp(T).
The closure of the eigenvalues is the spectrum of T restricted to Hpp. So
Comparison
A bounded self adjoint operator on Hilbert space is a bounded operator on a Banach space.Unlike the Banach space formulation, the union
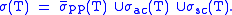
need not be disjoint. It is disjoint when the operator T is of uniform multiplicity, say m, i.e. if T is unitarily equivalent to multiplication by λ on the direct sum
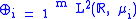
for some Borel measures
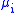. When more than one measure appears in the above expression, we see that it is possible for the union of the three types of spectra to not be disjoint. If λ ∈ σac(T) ∩ σpp(T), λ is sometimes called an eigenvalue embedded in the absolutely continuous spectrum.When T is unitarily equivalent to multiplication by λ on
the decomposition of σ(T) from Borel functional calculus is a refinement of the Banach space case.
Physics
The preceding comments can be extended to the unbounded self-adjoint operators since Riesz-Markov holds for locally compact Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s.
In quantum mechanics
Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
, observables are, not necessarily bounded, self adjoint operators and their spectra are the possible outcomes of measurements. Absolutely continuous spectrum of a physical observable corresponds to free state
Free state
Free state may refer to:* Free state , a loosely defined term used by various states at different times and places to describe themselves...
s of a system, while the pure point spectrum corresponds to bound state
Bound state
In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...
s. The singular spectrum correspond to physically impossible outcomes. An example of a quantum mechanical observable which has purely continuous spectrum is the position operator
Position operator
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. Consider, for example, the case of a spinless particle moving on a line. The state space for such a particle is L2, the Hilbert space of complex-valued and square-integrable ...
of a free particle moving on a line. Its spectrum is the entire real line. Also, since the momentum operator
Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once...
is unitarily equivalent to the position operator, via the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, they have the same spectrum.
Intuition may induce one to say that the discreteness of the spectrum is intimately related to the corresponding states being "localized". However, a careful mathematical analysis shows that this is not true. The following
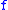
is an element of
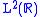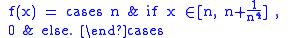
and increasing as .However, the phenomena of Anderson localization
Anderson localization
In condensed matter physics, Anderson localization, also known as strong localization, is the absence of diffusion of waves in a disordered medium. This phenomenon is named after the American physicist P. W...
and dynamical localization describe, when the eigenfunctions are localized in a physical sense. Anderson Localization means that eigenfunctions decay exponentially as
. Dynamical localization is more subtle to define.Sometimes, when performing physical quantum mechanical calculations, one encounters "eigenvectors" that do not lie in L2(R), i.e. wave functions that are not localized. These are the free states of the system. As stated above, in the mathematical formulation, the free states correspond to the absolutely continuous spectrum. Alternatively, if it is insisted that the notion of eigenvectors and eigenvalues survive the passage to the rigorous, one can consider operators on rigged Hilbert space
Rigged Hilbert space
In mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
s.
It was believed for some time that singular spectrum is something artificial. However, examples as the almost Mathieu operator and random Schrödinger operators have shown, that all types of spectra arise naturally in physics.