
Open mapping theorem (functional analysis)
Encyclopedia
In functional analysis
, the open mapping theorem, also known as the Banach–Schauder theorem (named after Stefan Banach
and Juliusz Schauder
), is a fundamental result which states that if a continuous linear operator between Banach space
s is surjective then it is an open map. More precisely, :
The proof uses the Baire category theorem
, and completeness of both X and Y is essential to the theorem. The statement of the theorem is no longer true if either space is just assumed to be a normed space, but is true if X and Y are taken to be Fréchet space
s.
Let U, V be the open unit balls in X, Y respectively. Then X is the union of the sequence of multiples of the unit ball, k ∈ N, and since A is surjective,

By the Baire category theorem
, the Banach space Y cannot be the union of countably many nowhere dense set
s, so there is such that the closure
of A(kU) has non-empty interior
. Thus, there is an open ball B(c, r) in Y, with center c and , contained in the closure of A(kU). If v ∈ V, then and c are in B(c, r), hence are limit points of . By continuity of addition, their difference rv is a limit point of . By linearity of A, this implies that any v ∈ V is in the closure of , where δ = . It follows that for any y ∈ Y and , there is an x ∈ X with:
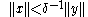 and
and 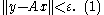
Fix (where δ V means the ball V stretched by a factor of δ, rather than the boundary of V). By (1), there is some with |||| < 1 and |||| . Define a sequence {xn} inductively as follows. Assume:
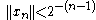 and
and 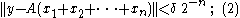
by (1) we can pick so that:
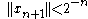 and
and 
so (2) is satisfied for . Let
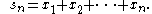
From the first inequality in (2), {sn} is a Cauchy sequence
, and since X is complete, sn converges to some . By (2), the sequence tends to y, and so by continuity of A. Also,
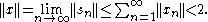
This shows that every belongs to , or equivalently, that the image A(U) of the unit ball in X contains the open ball . Hence, A(U) is a neighborhood of 0 in Y, and this concludes the proof.
s. Furthermore, the theorem can be combined with the Baire category theorem in the following manner :
Furthermore, in this latter case if N is the kernel
of A, then there is a canonical factorization of A in the form
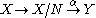
where is the quotient space
(also an F-space) of X by the closed
subspace N. The quotient mapping is open, and the mapping α is an isomorphism
of topological vector space
s .
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the open mapping theorem, also known as the Banach–Schauder theorem (named after Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
and Juliusz Schauder
Juliusz Schauder
Juliusz Paweł Schauder was a Polish mathematician of Jewish origin, known for his work in functional analysis, partial differential equation and mathematical physics.Born on September 21, 1899 in Lemberg, he had to fight in World War I right after his graduation from school...
), is a fundamental result which states that if a continuous linear operator between Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s is surjective then it is an open map. More precisely, :
- If X and Y are Banach spaces and A : X → Y is a surjective continuous linear operator, then A is an open map (i.e. if U is an open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in X, then A(U) is open in Y).
The proof uses the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
, and completeness of both X and Y is essential to the theorem. The statement of the theorem is no longer true if either space is just assumed to be a normed space, but is true if X and Y are taken to be Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s.
Consequences
The open mapping theorem has several important consequences:- If A : X → Y is a bijective continuous linear operator between the Banach spaces X and Y, then the inverse operatorInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
A-1 : Y → X is continuous as well (this is called the bounded inverse theoremBounded inverse theoremIn mathematics, the bounded inverse theorem is a result in the theory of bounded linear operators on Banach spaces. It states that a bijective bounded linear operator T from one Banach space to another has bounded inverse T−1. It is equivalent to both the open mapping theorem and the closed...
). - If A : X → Y is a linear operator between the Banach spaces X and Y, and if for every sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(xn) in X with xn → 0 and Axn → y it follows that y = 0, then A is continuous (Closed graph theoremClosed graph theoremIn mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
).
Proof
One has to prove that if is a continuous linear surjective map between Banach spaces, then A is an open map. It suffices to show that A maps the open unit ball in X to a neighborhood of the origin of Y.Let U, V be the open unit balls in X, Y respectively. Then X is the union of the sequence of multiples of the unit ball, k ∈ N, and since A is surjective,

By the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
, the Banach space Y cannot be the union of countably many nowhere dense set
Nowhere dense set
In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of rational numbers, as a subset of R has the property that the closure of the interior is empty, but it is not nowhere dense; in fact it...
s, so there is such that the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of A(kU) has non-empty interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
. Thus, there is an open ball B(c, r) in Y, with center c and , contained in the closure of A(kU). If v ∈ V, then and c are in B(c, r), hence are limit points of . By continuity of addition, their difference rv is a limit point of . By linearity of A, this implies that any v ∈ V is in the closure of , where δ = . It follows that for any y ∈ Y and , there is an x ∈ X with:
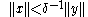 and
and 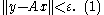
Fix (where δ V means the ball V stretched by a factor of δ, rather than the boundary of V). By (1), there is some with |||| < 1 and |||| . Define a sequence {xn} inductively as follows. Assume:
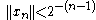 and
and 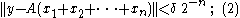
by (1) we can pick so that:
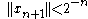 and
and 
so (2) is satisfied for . Let
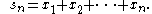
From the first inequality in (2), {sn} is a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
, and since X is complete, sn converges to some . By (2), the sequence tends to y, and so by continuity of A. Also,
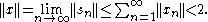
This shows that every belongs to , or equivalently, that the image A(U) of the unit ball in X contains the open ball . Hence, A(U) is a neighborhood of 0 in Y, and this concludes the proof.
Generalizations
Local convexity of X or Y is not essential to the proof, but completeness is: the theorem remains true in the case when X and Y are F-spaceF-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
s. Furthermore, the theorem can be combined with the Baire category theorem in the following manner :
- Let X be a F-space and Y a topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
. If is a continuous linear operator, then either A(X) is a meager set in Y, or A(X) = Y. In the latter case, A is an open mapping and Y is also an F-space.
Furthermore, in this latter case if N is the kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of A, then there is a canonical factorization of A in the form
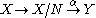
where is the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
(also an F-space) of X by the closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subspace N. The quotient mapping is open, and the mapping α is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s .

