
Position operator
Encyclopedia
In quantum mechanics
, the position operator is the operator
that corresponds to the position observable
of a particle. Consider, for example, the case of a spin
less particle moving on a line. The state space
for such a particle is L2(R)
, the Hilbert space
of complex-valued and square-integrable (with respect to the Lebesgue measure
) functions on the real line. The position operator, Q, is then defined by
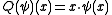
with domain
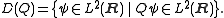
Since all continuous function
s with compact support lie in D(Q), Q is densely defined
. Q, being simply multiplication by x, is a self adjoint operator, thus satisfying the requirement of a quantum mechanical observable. Immediately from the definition we can deduce that the spectrum consists of the entire real line
and that Q has purely continuous spectrum
, therefore no discrete eigenvalues. The three dimensional case is defined analogously. We shall keep the one-dimensional assumption in the following discussion.
, in order to discuss measurement
, we need to calculate the spectral resolution of Q:

Since Q is just multiplication by x, its spectral resolution is simple. For a Borel subset B of the real line, let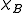 denote the indicator function of B. We see that the projection-valued measure
denote the indicator function of B. We see that the projection-valued measure
ΩQ is given by
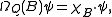
i.e. ΩQ is multiplication by the indicator function of B. Therefore, if the system is prepared in state ψ, then the probability
of the measured position of the particle being in a Borel set
B is

where μ is the Lebesgue measure. After the measurement, the wave function collapses to either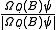 or
or 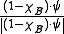 , where
, where  is the Hilbert space norm on L2(R).
is the Hilbert space norm on L2(R).
P is defined by

usually written in bra-ket notation
as:
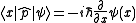
with appropriate domain. P and Q are unitarily equivalent, with the unitary operator
being given explicitly by the Fourier transform
. Thus they have the same spectrum. In physical language, P acting on momentum space wave functions is the same as Q acting on position space wave functions (under the image of Fourier transform).
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the position operator is the operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
that corresponds to the position observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
of a particle. Consider, for example, the case of a spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
less particle moving on a line. The state space
State space (physics)
In physics, a state space is a complex Hilbert space within which the possible instantaneous states of the system may be described by a unit vector. These state vectors, using Dirac's bra-ket notation, can often be treated as vectors and operated on using the rules of linear algebra...
for such a particle is L2(R)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of complex-valued and square-integrable (with respect to the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
) functions on the real line. The position operator, Q, is then defined by
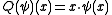
with domain
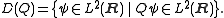
Since all continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s with compact support lie in D(Q), Q is densely defined
Densely-defined operator
In mathematics — specifically, in operator theory — a densely defined operator is a type of partially defined function; in a topological sense, it is a linear operator that is defined "almost everywhere"...
. Q, being simply multiplication by x, is a self adjoint operator, thus satisfying the requirement of a quantum mechanical observable. Immediately from the definition we can deduce that the spectrum consists of the entire real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
and that Q has purely continuous spectrum
Continuous spectrum
The spectrum of a linear operator is commonly divided into three parts: point spectrum, continuous spectrum, and residual spectrum.If H is a topological vector space and A:H \to H is a linear map, the spectrum of A is the set of complex numbers \lambda such that A - \lambda I : H \to H is not...
, therefore no discrete eigenvalues. The three dimensional case is defined analogously. We shall keep the one-dimensional assumption in the following discussion.
Measurement
As with any quantum mechanical observableObservable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
, in order to discuss measurement
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
, we need to calculate the spectral resolution of Q:

Since Q is just multiplication by x, its spectral resolution is simple. For a Borel subset B of the real line, let
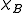 denote the indicator function of B. We see that the projection-valued measure
denote the indicator function of B. We see that the projection-valued measureProjection-valued measure
In mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
ΩQ is given by
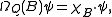
i.e. ΩQ is multiplication by the indicator function of B. Therefore, if the system is prepared in state ψ, then the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of the measured position of the particle being in a Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
B is

where μ is the Lebesgue measure. After the measurement, the wave function collapses to either
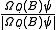 or
or 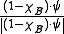 , where
, where  is the Hilbert space norm on L2(R).
is the Hilbert space norm on L2(R).Unitary equivalence with momentum operator
For a particle on a line, the momentum operatorMomentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once...
P is defined by

usually written in bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
as:
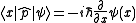
with appropriate domain. P and Q are unitarily equivalent, with the unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
being given explicitly by the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. Thus they have the same spectrum. In physical language, P acting on momentum space wave functions is the same as Q acting on position space wave functions (under the image of Fourier transform).

