Complete group
Encyclopedia
In mathematics
, a group
G is said to be complete if every automorphism
of G is inner
, and the group is a centerless group; that is, it has a trivial outer automorphism group
and trivial center
.
Equivalently, a group is complete if the conjugation map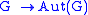
(sending an element g to conjugation by g) is an isomorphism: 1-to-1 corresponds to centerless, onto corresponds to no outer automorphisms.
s Sn are complete except when n = 2 or 6. For the case n = 2 the group has a nontrivial center, while for the case n = 6 there is an outer automorphism.
The automorphism group of a simple group G is an almost simple group
;
for a nonabelian simple group
G, the automorphism group of G is complete.
to its automorphism group (via sending an element to conjugation by that element), although the reverse need not hold: for example, the dihedral group
of eight elements is isomorphic to its automorphism group, but it is not complete. For a discussion, see .
with kernel
N and quotient G' . If the kernel N is a complete group then the extension splits: G is isomorphic to the direct product
N × G'. A proof using homomorphisms and exact sequences can be given in a natural way: The action of G (by conjugation
) on the normal subgroup N gives rise to a group homomorphism
. Since Out(N) = 1 and N has trivial center the homomorphism φ is surjective and has an obvious section given by the inclusion of N in G. The kernel of φ is the centralizer CG(N) of N in G, and so G is at least a semidirect product
CG(N) ⋊ N, but the action of N on CG(N) is trivial, and so the product is direct. This proof is somewhat interesting since the original exact sequence is reversed during the proof.
This can be restated in terms of elements and internal conditions: If N is a normal, complete subgroup of a group G, then G = CG(N) × N is a direct product. The proof follows directly from the definition: N is centerless giving CG(N) ∩ N is trivial. If g is an element of G then it induces an automorphism of N by conjugation, but N = Aut(N) and this conjugation must be equal to conjugation by some element n of N. Then conjugation by gn-1 is the identity on N and so gn-1 is in CG(N) and every element g of G is a product (gn-1)n in CG(N)N.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is said to be complete if every automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of G is inner
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
, and the group is a centerless group; that is, it has a trivial outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
and trivial center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
.
Equivalently, a group is complete if the conjugation map
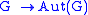(sending an element g to conjugation by g) is an isomorphism: 1-to-1 corresponds to centerless, onto corresponds to no outer automorphisms.Examples
As an example, all the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
s Sn are complete except when n = 2 or 6. For the case n = 2 the group has a nontrivial center, while for the case n = 6 there is an outer automorphism.
The automorphism group of a simple group G is an almost simple group
Almost simple group
In mathematics, a group is said to be almost simple if it contains a non-abelian simple group and is contained within the automorphism group of that simple group: if it fits between a simple group and its automorphism group.More precisely, a group is almost simple if it is isomorphic to such a group...
;
for a nonabelian simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
G, the automorphism group of G is complete.
Properties
A complete group is always isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to its automorphism group (via sending an element to conjugation by that element), although the reverse need not hold: for example, the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of eight elements is isomorphic to its automorphism group, but it is not complete. For a discussion, see .
Extensions of complete groups
Assume that a group G is a group extension given as a short exact sequence of groupswith kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
N and quotient G' . If the kernel N is a complete group then the extension splits: G is isomorphic to the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
N × G'. A proof using homomorphisms and exact sequences can be given in a natural way: The action of G (by conjugation
Conjugation
Conjugation or conjugate may refer to:* Conjugation , the modification of a verb from its basic form* Conjugate , used to rationalize the denominator of a fraction...
) on the normal subgroup N gives rise to a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
. Since Out(N) = 1 and N has trivial center the homomorphism φ is surjective and has an obvious section given by the inclusion of N in G. The kernel of φ is the centralizer CG(N) of N in G, and so G is at least a semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
CG(N) ⋊ N, but the action of N on CG(N) is trivial, and so the product is direct. This proof is somewhat interesting since the original exact sequence is reversed during the proof.
This can be restated in terms of elements and internal conditions: If N is a normal, complete subgroup of a group G, then G = CG(N) × N is a direct product. The proof follows directly from the definition: N is centerless giving CG(N) ∩ N is trivial. If g is an element of G then it induces an automorphism of N by conjugation, but N = Aut(N) and this conjugation must be equal to conjugation by some element n of N. Then conjugation by gn-1 is the identity on N and so gn-1 is in CG(N) and every element g of G is a product (gn-1)n in CG(N)N.