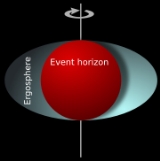
|
|
|
|
Kerr metric
|
| |
|
| |
In general relativity, the Kerr metric (or Kerr vacuum) describes the geometry of spacetime around a rotating massive body. According to this metric, such rotating bodies should exhibit frame dragging, an unusual prediction of general relativity; measurement of this frame dragging effect is a major goal of the Gravity Probe B experiment. Roughly speaking, this effect predicts that objects coming close to a rotating mass will be entrained to participate in its rotation, not because of any applied force or torque that can be felt, but rather because the curvature of spacetime associated with rotating bodies.
Discussion
Ask a question about 'Kerr metric' Start a new discussion about 'Kerr metric' Answer questions from other users |
Encyclopedia
In general relativity, the Kerr metric (or Kerr vacuum) describes the geometry of spacetime around a rotating massive body. According to this metric, such rotating bodies should exhibit frame dragging, an unusual prediction of general relativity; measurement of this frame dragging effect is a major goal of the Gravity Probe B experiment. Roughly speaking, this effect predicts that objects coming close to a rotating mass will be entrained to participate in its rotation, not because of any applied force or torque that can be felt, but rather because the curvature of spacetime associated with rotating bodies. At close enough distances, all objects — even light itself — must rotate with the body; the region where this holds is called the ergosphere.
The Kerr metric is often used to describe rotating black holes, which exhibit even more exotic phenomena. Such black holes have two surfaces where the metric appears to have a singularity; the size and shape of these surfaces depends on the black hole's mass and angular momentum. The outer surface encloses the ergosphere and has a shape similar to a flattened sphere. The inner surface is spherical and marks the "radius of no return" also called the "event horizon"; objects passing through this radius can never again communicate with the world outside that radius. However, neither surface is a true singularity, since their apparent singularity can be eliminated in a different coordinate system. Objects between these two horizons must co-rotate with the rotating body, as noted above; this feature can be used to extract energy from a rotating black hole, up to its invariant mass energy, Mc2. Even stranger phenomena can be observed within the innermost region of this spacetime, such as some forms of time travel. For example, the Kerr metric permits closed, time-like loops in which a band of travellers returns to the same place after moving for a finite time by their own clock; however, they return to the same place and time, as seen by an outside observer.
The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. The Kerr metric is a generalization of the Schwarzschild metric, which was discovered by Karl Schwarzschild in 1916 and which describes the geometry of spacetime around an uncharged, perfectly spherical, and non-rotating body. The corresponding solution for a charged, spherical, non-rotating body, the Reissner-Nordström metric, was discovered shortly after (1916-1918). However, the exact solution for an uncharged, rotating body, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr. The natural extension to a charged, rotating body, the Kerr-Newman metric, was discovered shortly afterwards in 1965. These four related solutions may be summarized by the following table:
where Q represents the body's electric charge and J represents its spin angular momentum.
Mathematical form
The Kerr metric describes the geometry of spacetime in the vicinity of a mass M rotating with angular momentum J
where the coordinates are standard spherical coordinate system, and rs is the Schwarzschild radius
and where the length-scales a, ? and ? have been introduced for brevity
In the non-relativistic limit where M (or, equivalently, rs) goes to zero, the Kerr metric becomes the orthogonal metric for the oblate spheroidal coordinates
which are equivalent to the Boyer-Lindquist coordinates
Frame dragging
We may rewrite the Kerr metric in the following form
This metric is equivalent to a co-rotating reference frame that is rotating with angular speed O that depends on both the radius r and the colatitude ?
Thus, an inertial reference frame is entrained by the rotating central mass to participate in the latter's rotation; this is frame-dragging, which has been observed experimentally.
Important surfaces
The Kerr metric has two surfaces on which it appears to be singular. The inner surface corresponds to a spherical event horizon similar to that observed in the Schwarzschild metric; this occurs where the purely radial component grr of the metric goes to infinity. Solving the quadratic equation 1/grr = 0 yields the solution
Another singularity occurs where the purely temporal component gtt of the metric changes sign from positive to negative. Again solving a quadratic equation gtt=0 yields the solution
Due to the cos2? term in the square root, this outer surface resembles a flattened sphere that touches the inner surface at the poles of the rotation axis, where the colatitude ? equals 0 or p; the space between these two surfaces is called the ergosphere. There are two other solutions to these quadratic equations, but they lie within the event horizon, where the Kerr metric is not used, since it has unphysical properties (see below).
A moving particle experiences a positive proper time along its worldline, its path through spacetime. However, this is impossible within the ergosphere, where gtt is negative, unless the particle is co-rotating with the interior mass M with an angular speed at least of O. Thus, no particle can rotate opposite to the central mass within the ergosphere.
As with the event horizon in the Schwarzschild metric the apparent singularities at rinner and router are an illusion created by the choice of coordinates (i.e., they are coordinate singularities). In fact, the space-time can be smoothly continued through them by an appropriate choice of coordinates.
Ergosphere and the Penrose process
A black hole in general is surrounded by a spherical surface, the event horizon situated at the Schwarzschild radius (for a nonrotating black hole), where the escape velocity is equal to the velocity of light. Within this surface, no observer/particle can maintain itself at a constant radius. It is forced to fall inwards, and so this is sometimes called the static limit.
A rotating black hole has the same static limit at the Schwarzschild radius but there is an additional surface outside the Schwarzschild radius named the "ergosurface" given by in Boyer-Lindquist coordinates, which can be intuitively characterized as the sphere where "the rotational velocity of the surrounding space" is dragged along with the velocity of light. Within this sphere the dragging is greater than the speed of light, and any observer/particle is forced to co-rotate.
The region outside the event horizon but inside the sphere where the rotational velocity is the speed of light, is called the ergosphere (from Greek ergon meaning work). Particles falling within the ergosphere are forced to rotate faster and thereby gain energy. Because they are still outside the event horizon, they may escape the black hole. The net process is that the rotating black hole emits energetic particles at the cost of its own total energy. The possibility of extracting spin energy from a rotating black hole was first proposed by the mathematician Roger Penrose in 1969 and is thus called the Penrose process. Rotating black holes in astrophysics are a potential source of large amounts of energy and are used to explain energetic phenomena, such as gamma ray bursts.
Gradient operator
Since even a direct check on the Kerr metric involves cumbersome calculations, the contravariant components of the metric tensor are shown below in the expression for the square of the four-gradient operator:
Features of the Kerr vacuum
The Kerr vacuum exhibits many noteworthy features: the maximal analytic extension includes a sequence of asymptotically flat exterior regions, each associated with an ergosphere, stationary limit surfaces, event horizons, Cauchy horizons, closed timelike curves, and a ring-shaped curvature singularity. The geodesic equation can be solved exactly in closed form. In addition to two Killing vector fields (corresponding to time translation and axisymmetry), the Kerr vacuum admits a remarkable Killing tensor. There is a pair of principal null congruences (one ingoing and one outgoing). The Weyl tensor is algebraically special, in fact it has Petrov type D. The global structure is known. Topologically, the homotopy type of the Kerr spacetime can be simply characterized as a line with circles attached at each integer point.
While the Kerr vacuum is an exact axis-symmetric solution to solution is probably not axis-symmetric. The instability of the Kerr metric in the interior region implies that many of the features of the Kerr vacuum described above would probably not be present in a black hole that came into being through gravitational collapse.
A surface on which light can orbit a black hole is called a photon sphere. The Kerr solution has infinitely many photon spheres, lying between an inner one and an outer one. In the nonrotating, Schwarzschild solution, with a=0, the inner and outer photon spheres degenerate, so that all the photons sphere occur at the same radius. The greater the spin of the black hole is, the farther from each other the inner and outer photon spheres move. A beam of light travelling in a direction opposite to the spin of the black hole will circularly orbit the hole at the outer photon sphere. A beam of light travelling in the same direction as the black hole's spin will circularly orbit at the inner photon sphere. Orbiting geodesics with some angular momentum perpendicular to the axis of rotation of the black hole will orbit on photon spheres between these two extremes. Because the space-time is rotating, such orbits exhibit a precession, since there is a shift in the variable after completing one period in the variable.
Overextreme Kerr solutions
The location of the event horizon is determined by the larger root of . When , there are no (real valued) solutions to this equation, and there is no event horizon. With no event horizons to hide it from the rest of the universe, the black hole ceases to be a black hole and will instead be a naked singularity.
Kerr black holes as wormholes
Although the Kerr solution appears to be singular at the roots of , these are actually coordinate singularities, and, with an appropriate choice of new coordinates, the Kerr solution can be smoothly extended through the values of corresponding to these roots. The larger of these roots determines the location of the event horizon, and the smaller determines the location of a Cauchy horizon. A (future-directed, time-like) curve can start in the exterior and pass through the event horizon. Once having passed thrugh the event horizon, the coordinate now behaves like a time coordinate, so it must decrease until the curve passes through the Cauchy horizon.
The region beyond the Cauchy horizon has several surprising features. The coordinate again behaves like a spatial coordinate and can vary freely. The interior region has a reflection symmetry, so that a (future-directed time-like) curve may continue along a symmetric path, which continues through a second Cauchy horizon, through a second event horizon, and out into a new exterior region which is isometric to the original exterior region of the Kerr solution. The curve could then escape to infinity in the new region or enter the future event horizon of the new exterior region and repeat the process. This second exterior is sometimes thought of as another universe. On the other hand, in the Kerr solution, the singularity at is a ring, and the curve may pass through the center of this ring. The region beyond permits closed, time-like curves. Since the trajectory of observers and particles in general relativity are described by time-like curves, it is possible for observers in this region to return to their past.
While it is expected that the exterior region of the Kerr solution is stable, and that all rotating black holes will eventually approach a Kerr metric, the interior region of the solution appears to be unstable, much like a pencil balanced on its point (Penrose 1968).
Relation to other exact solutions
The Kerr vacuum is a particular example of a stationary axially symmetric vacuum solution to the Einstein field equation. The family of all stationary axially symmetric vacuum solutions to the Einstein field equation are the Ernst vacuums.
The Kerr solution is also related to various non-vacuum solutions which model black holes. For example, the Kerr-Newman electrovacuum models a (rotating) black hole endowed with an electric charge, while the Kerr-Vaidya null dust models a (rotating) hole with infalling electromagnetic radiation.
The special case of the Kerr metric yields the Schwarzschild metric, which models a nonrotating black hole which is static and spherically symmetric, in the Schwarzschild coordinates. (In this case, every Geroch moment but the mass vanishes.)
The interior of the Kerr vacuum, or rather a portion of it, is locally isometric to the Chandrasekhar/Ferrari CPW vacuum, an example of a colliding plane wave model. This is particularly interesting, because the global structure of this CPW solution is quite different from that of the Kerr vacuum, and in principle, an experimenter could hope to study the geometry of (the outer portion of) the Kerr interior by arranging the collision of two suitable gravitational plane waves.
Multipole moments
Each asymptotically flat Ernst vacuum can be characterized by giving the infinite sequence of relativistic multipole moments, the first two of which can be interpreted as the mass and angular momentum of the source of the field. There are alternative formulations of relativistic multipole moments due to Hansen, Thorne, and Geroch, which turn out to agree with each other. The relativistic multipole moments of the Kerr vacuum were computed by Hansen; they turn out to be
Thus, the special case of the Schwarzschild vacuum (a=0) gives the "monopole point source" of general relativity.
Warning: do not confuse these relativistic multipole moments with the Weyl multipole moments, which arise from treating a certain metric function (formally corresponding to Newtonian gravitational potential) which appears the Weyl-Papapetrou chart for the Ernst family of all stationary axisymmetric vacuums solutions using the standard euclidean scalar multipole moments. In a sense, the Weyl moments only (indirectly) characterize the "mass distribution" of an isolated source, and they turn out to depend only on the even order relativistic moments. In the case of solutions symmetric across the equatorial plane the odd order Weyl moments vanish. For the Kerr vacuum solutions, the first few Weyl moments are given by
In particular, we see that the Schwarzschild vacuum has nonzero second order Weyl moment, corresponding to the fact that the "Weyl monopole" is the Chazy-Curzon vacuum solution, not the Schwarzschild vacuum solution, which arises from the Newtonian potential of a certain finite length uniform density thin rod.
In weak field general relativity, it is convenient to treat isolated sources using another type of multipole, which generalize the Weyl moments to mass multipole moments and momentum multipole moments, characterizing respectively the distribution of mass and of momentum of the source. These are multi-indexed quantities whose suitably symmetrized (anti-symmetrized) parts can be related to the real and imaginary parts of the relativistic moments for the full nonlinear theory in a rather complicated manner.
Perez and Moreschi have given an alternative notion of "monopole solutions" by expanding the standard NP tetrad of the Ernst vacuums in powers of r (the radial coordinate in the Weyl-Papapetrou chart). According to this formulation:
- the isolated mass monopole source with zero angular momentum is the Schwarzschild vacuum family (one parameter),
- the isolated mass monopole source with radial angular momentum is the Taub-NUT vacuum family (two parameters; not quite asymptotically flat),
- the isolated mass monopole source with axial angular momentum is the Kerr vacuum family (two parameters).
In this sense, the Kerr vacuums are the simplest stationary axisymmetric asymptotically flat vacuum solutions in general relativity.
Open problems
The Kerr vacuum is often used as a model of a black hole, but if we hold the solution to be valid only outside some compact region (subject to certain restrictions), in principle we should be able to use it as an exterior solution to model the gravitational field around a rotating massive object other than a black hole, such as a neutron star--- or the Earth. This works out very nicely for the non-rotating case, where we can match the Schwarzschild vacuum exterior to a Schwarzschild fluid interior, and indeed to more general static spherically symmetric perfect fluid solutions. However, the problem of finding a rotating perfect-fluid interior which can be matched to a Kerr exterior, or indeed to any asymptotically flat vacuum exterior solution, has proven very difficult. In particular, the Wahlquist fluid, which was once thought to be a candidate for matching to a Kerr exterior, is now known not to admit any such matching. At present it seems that only approximate solutions modeling slowly rotating fluid balls (the relativistic analog of oblate spheroidal balls with nonzero mass and angular momentum but vanishing higher multipole moments) are known. However, the exterior of the Neugebauer/Meinel disk, an exact dust solution which models a rotating thin disk, approaches in a limiting case the a=M Kerr vacuum.
The equations of the trajectory and the time dependence for a particle in the Kerr field
In the Hamilton-Jacobi equation we write the action S in the form:
where , m, and L are the conserved energy, the rest mass and the component of the angular momentum (along the axis of symmetry of the field) of the particle consecutively, and carry out the separation of variables in the Hamilton Jacobi equation as follows:
-
where K is a new arbitrary constant. The equation of the trajectory and the time dependence of the coordinates along the trajectory (motion equation) can be found then easily and directly from these equations:
-
See also
Further reading
- See chapter 19 for a readable introduction at the advanced undergraduate level.
- See chapters 6--10 for a very thorough study at the advanced graduate level.
- See chapter 13 for the Chandrasekhar/Ferrari CPW model.
- See chapter 7.* Characterization of three standard families of vacuum solutions as noted above.
- Gives the relativistic multipole moments for the Ernst vacuums (plus the electromagnetic and gravitational relativistic multipole moments for the charged generalization).*
|
| |
|
|
