
Cardinal function
Encyclopedia
In mathematics, a cardinal function (or cardinal invariant) is a function that returns cardinal number
s.
as a tool for describing various topological properties. Below are some examples. (Note: some authors, arguing that "there are no finite cardinal numbers in general topology", prefer to define the cardinal functions listed below so that they never taken on finite cardinal numbers as values; this requires modifying some of the definitions given below, e.g. by adding "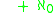 " to the right-hand side of the definitions, etc.)
" to the right-hand side of the definitions, etc.)
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s.
Cardinal functions in set theory
- The most frequently used cardinal function is a function which assigns to a set "A" its cardinality, denoted by | A |.
- Aleph numberAleph numberIn set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
s and beth numberBeth numberIn mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
s can both be seen as cardinal functions defined on ordinal numberOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s.
- Cardinal arithmetic operations are examples of functions from cardinal numbers (or pairs of them) to cardinal numbers.
- Cardinal characteristics of a (proper) idealIdeal (set theory)In the mathematical field of set theory, an ideal is a collection of sets that are considered to be "small" or "negligible". Every subset of an element of the ideal must also be in the ideal , and the union of any two elements of the ideal must also be in the ideal.More formally, given a set X, an...
I of subsets of X are: .
.
-
- The "additivity" of I is the smallest number of sets from I whose union is not in I any more. As any ideal is closed under finite unions, this number is always at least
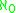 ; if I is a σ-ideal, then add(I)≥
; if I is a σ-ideal, then add(I)≥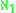 .
.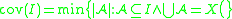 .
. - The "covering number" of I is the smallest number of sets from I whose union is all of X. As X itself is not in I, we must have add(I) ≤ cov(I).
 ,
, - The "uniformity number" of I (sometimes also written
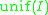 ) is the size of the smallest set not in I. Assuming I contains all singletons, add(I) ≤ non(I).
) is the size of the smallest set not in I. Assuming I contains all singletons, add(I) ≤ non(I).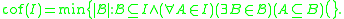
- The "cofinality" of I is the cofinalityCofinalityIn mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
of the partial order (I, ⊆). It is easy to see that we must have non(I) ≤ cof(I) and cov(I) ≤ cof(I).
- The "additivity" of I is the smallest number of sets from I whose union is not in I any more. As any ideal is closed under finite unions, this number is always at least
- For a preordered set
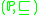 the bounding number
the bounding number 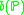 and dominating number
and dominating number 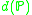 is defined as
is defined as
-
 ,
,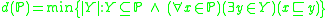
- In PCF theoryPCF theoryPCF theory is the name of a mathematical theory, introduced by Saharon , that deals with the cofinality of the ultraproducts of ordered sets. It gives strong upper bounds on the cardinalities of power sets of singular cardinals, and has many more applications as well...
the cardinal function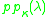 is used.
is used.
Cardinal functions in topology
Cardinal functions are widely used in topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
as a tool for describing various topological properties. Below are some examples. (Note: some authors, arguing that "there are no finite cardinal numbers in general topology", prefer to define the cardinal functions listed below so that they never taken on finite cardinal numbers as values; this requires modifying some of the definitions given below, e.g. by adding "
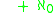 " to the right-hand side of the definitions, etc.)
" to the right-hand side of the definitions, etc.)- Perhaps the simplest cardinal invariants of a topological space X are its cardinality and the cardinality of its topology, denoted respectively by |X | and o(X).
- The weight w(X ) of a topological space X is the cardinality of the smallest baseBase (topology)In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for X. When w(X ) =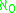 the space X is said to be second countable.
the space X is said to be second countable.
- The
 -weight of a space X is the cardinality of the smallest
-weight of a space X is the cardinality of the smallest  -base for X.
-base for X.
- The
- The character of a topological space X at a point x is the cardinality of the smallest local base for x. The character of space X is

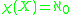 the space X is said to be first countable.
the space X is said to be first countable. - The density d(X ) of a space X is the cardinality of the smallest dense subset of X. When
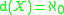 the space X is said to be separable.
the space X is said to be separable. - The cellularity of a space X is
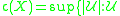 is a familyFamily of setsIn set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
is a familyFamily of setsIn set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
of mutually disjoint non-empty openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subsets of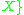 .
.- The Hereditary cellularity (sometimes spread) is the least upper bound of cellularities of its subsets:
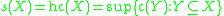
 with the subspace topology is discrete
with the subspace topology is discrete 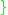 .
.
- The Hereditary cellularity (sometimes spread) is the least upper bound of cellularities of its subsets:
- The tightness t(x, X) of a topological space X at a point
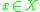 is the smallest cardinal number
is the smallest cardinal number  such that, whenever
such that, whenever  for some subset Y of X, there exists a subset Z of Y, with |Z | ≤
for some subset Y of X, there exists a subset Z of Y, with |Z | ≤  , such that
, such that  . Symbolically,
. Symbolically, 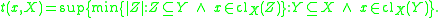
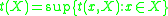 . When t(X) =
. When t(X) = 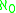 the space X is said to be countably generatedCountably generatedIn mathematics, the term countably generated can have several meanings:* An algebraic structure having countably many generators, see generating set...
the space X is said to be countably generatedCountably generatedIn mathematics, the term countably generated can have several meanings:* An algebraic structure having countably many generators, see generating set...
or countably tight.- The augumented tightness of a space X,
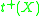 is the smallest regular cardinalRegular cardinalIn set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
is the smallest regular cardinalRegular cardinalIn set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
 such that for any
such that for any 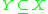 ,
,  there is a subset Z of Y with cardinality less than
there is a subset Z of Y with cardinality less than  , such that
, such that 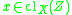 .
.
- The augumented tightness of a space X,
Basic inequalities
- c(X) ≤ d(X) ≤ w(X) ≤ o(X) ≤ 2|X|
-
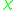 (X) ≤ w(X)
(X) ≤ w(X)
Cardinal functions in Boolean algebras
Cardinal functions are often used in the study of Boolean algebras.. We can mention, for example, the following functions:- Cellularity
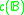 of a Boolean algebra
of a Boolean algebra 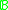 is the supremum of the cardinalities of antichainAntichainIn mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
is the supremum of the cardinalities of antichainAntichainIn mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
s in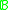 .
. - Length
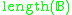 of a Boolean algebra
of a Boolean algebra  is
is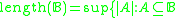 is a chain
is a chain 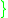
- Depth
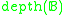 of a Boolean algebra
of a Boolean algebra 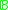 is
is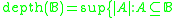 is a well-ordered subset
is a well-ordered subset  .
. - Incomparability
 of a Boolean algebra
of a Boolean algebra 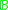 is
is such that
such that 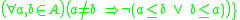 .
. - Pseudo-weight
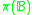 of a Boolean algebra
of a Boolean algebra 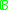 is
is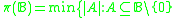 such that
such that 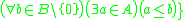 .
.
Cardinal functions in algebra
Examples of cardinal functions in algebra are:- Index of a subgroupIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
H of G is the number of cosets. - Dimension of a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is the cardinality of any Hamel basis of V. - More generally, for a free moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M over a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R we define rank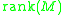 as the cardinality of any basis of this module.
as the cardinality of any basis of this module. - For a linear subspaceLinear subspaceThe concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
W of a vector space V we define codimensionCodimensionIn mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
of W (with respect to V). - For any algebraic structureAlgebraic structureIn abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
it is possible to consider the minimal cardinality of generators of the structure. - For algebraic extensionAlgebraic extensionIn abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
s algebraic degreeDegree of a field extensionIn mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
and separable degree are often employed (note that the algebraic degree equals the dimension of the extension as a vector space over the smaller field). - For non-algebraic field extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s transcendence degreeTranscendence degreeIn abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
is likewise used.
External links
- A Glossary of Definitions from General Topology http://math.berkeley.edu/~apollo/topodefs.ps

