
Born coordinates
Encyclopedia

Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. It is often used to analyze the physical experience of observers who ride on a ring or disk rigidly rotating at relativistic speeds
Ehrenfest paradox
The Ehrenfest paradox concerns the rotation of a "rigid" disc in the theory of relativity.In its original formulation as presented by Paul Ehrenfest 1909 in the Physikalische Zeitschrift, it discusses an ideally rigid cylinder that is made to rotate about its axis of symmetry...
. This chart is often attributed to Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
, due to his 1909 work on the relativistic physics of a rotating body – see Born rigidity
Born rigidity
Born rigidity, proposed by and later named after Max Born, is a concept in special relativity. It is one answer to the question of what, in special relativity, corresponds to the rigid body of non-relativistic classical mechanics....
.
Langevin observers in the cylindrical chart
To motivate the Born chart, we first consider the family of Langevin observers represented in an ordinary cylindrical coordinate chart for Minkowski spacetime. The world lines of these observers form a timelike congruenceCongruence (general relativity)
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
which is rigid in the sense of having a vanishing expansion tensor. They represent observers who rotate rigidly around an axis of cylindrical symmetry.
From the line element
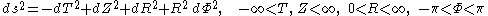
we can immediately read off a frame field
Frame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
representing the local Lorentz frames of stationary (inertial) observers
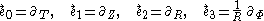
Here,
 is a timelike unit vector field
is a timelike unit vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
while the others are spacelike unit vector fields; at each event, all four are mutually orthogonal and determine the infinitesimal Lorentz frame of the static observer whose world line passes through that event.
Simultaneously boosting these frame fields in the
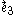 direction, we obtain the desired frame field describing the physical experience of the Langevin observers, namely
direction, we obtain the desired frame field describing the physical experience of the Langevin observers, namely
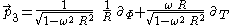
This frame was apparently first introduced (implicitly) by Paul Langevin
Paul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
in 1935; its first explicit use appears to have been by T. A. Weber, as recently as 1997! It is defined on the region 0 < R < 1/ω; this limitation is fundamental, since near the outer boundary, the velocity of the Langevin observers approaches the speed of light.
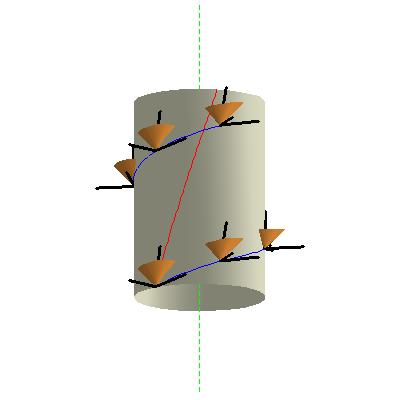
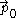 appears in the cylindrical chart as a helix
appears in the cylindrical chart as a helixHelix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
with constant radius (such as the red curve in the figure at right). Suppose we choose one Langevin observer and consider the other observers who ride on a ring of radius R which is rigidly rotating with angular velocity ω. Then if we take an integral curve (blue helical curve in the figure at right) of the spacelike basis vector
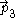 , we obtain a curve which we might hope can be interpreted as a "line of simultaneity" for the ring-riding observers. But as we see from the figure, ideal clocks carried by these ring-riding observers cannot be synchronized. This is our first hint that it is not as easy as one might expect to define a satisfactory notion of spatial geometry even for a rotating ring, much less a rotating disk!
, we obtain a curve which we might hope can be interpreted as a "line of simultaneity" for the ring-riding observers. But as we see from the figure, ideal clocks carried by these ring-riding observers cannot be synchronized. This is our first hint that it is not as easy as one might expect to define a satisfactory notion of spatial geometry even for a rotating ring, much less a rotating disk!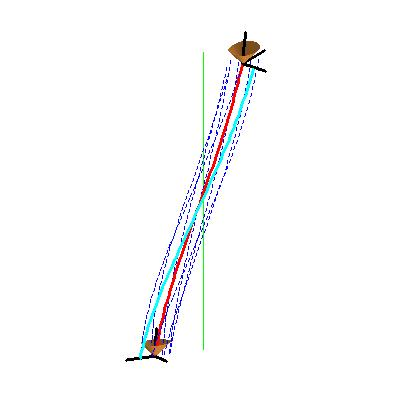
Congruence (general relativity)
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
of the Langevin congruence, we find that the acceleration vector
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
is
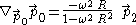
This points radially inward and it depends only on the (constant) radius of each helical world line. The expansion tensor vanishes identically, which means that nearby Langevin observers maintain constant distance from each other. The vorticity vector is
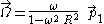
which is parallel to the axis of symmetry. This means that the world lines of the nearest neighbors of each Langevin observer are twisting about its own world line, as suggested by the figure at right. This is a kind of local
notion of "swirling" or vorticity.
In contrast, note that projecting the helices onto any one of the spatial hyperslices
 orthogonal to the world lines of the static observers gives a circle
orthogonal to the world lines of the static observers gives a circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, which is of course a closed curve. Even better, the coordinate basis vector
 is a spacelike Killing vector field whose integral curves are closed spacelike curves (circles, in fact), which moreover degenerate to zero length closed curves on the axis R = 0. This expresses the fact that our spacetime exhibits cylindrical symmetry, and also exhibits a kind of global notion of the rotation of our Langevin observers.
is a spacelike Killing vector field whose integral curves are closed spacelike curves (circles, in fact), which moreover degenerate to zero length closed curves on the axis R = 0. This expresses the fact that our spacetime exhibits cylindrical symmetry, and also exhibits a kind of global notion of the rotation of our Langevin observers.In the figure, the magenta curve shows how the spatial vectors
 are spinning about
are spinning about 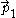 (which is suppressed in the figure since the Z coordinate is inessential). That is, the vectors
(which is suppressed in the figure since the Z coordinate is inessential). That is, the vectors 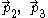 are not Fermi-Walker transported along the world line, so the Langevin frame is spinning as well as non-inertial. In other words, in our straightforward derivation of the Langevin frame, we kept the frame aligned with the radial coordinate basis vector
are not Fermi-Walker transported along the world line, so the Langevin frame is spinning as well as non-inertial. In other words, in our straightforward derivation of the Langevin frame, we kept the frame aligned with the radial coordinate basis vector 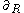 . By introducing a constant rate rotation of the frame carried by each Langevin observer about
. By introducing a constant rate rotation of the frame carried by each Langevin observer about  , we could, if we wished "despin" our frame to obtain a gyrostabilized version.
, we could, if we wished "despin" our frame to obtain a gyrostabilized version.Transforming to the Born chart
To obtain the Born chart, we straighten out the helical world lines of the Langevin observers using the simple coordinate transformation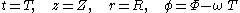
The new line element is

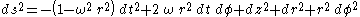
Notice the "cross-terms" involving
 , which show that the Born chart is not an orthogonal coordinate chart. The Born coordinates are also sometimes referred to as rotating cylindrical coordinates.
, which show that the Born chart is not an orthogonal coordinate chart. The Born coordinates are also sometimes referred to as rotating cylindrical coordinates.In the new chart, the world lines of the Langevin observers appear as vertical straight lines. Indeed, we can easily transform the four vector fields making up the Langevin frame into the new chart. We obtain
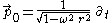

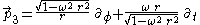
These are exactly the same vector fields as before--- they are now simply represented in a different coordinate chart!
Needless to say, in the process of "unwinding" the world lines of the Langevin observers, which appear as helices in the cylindrical chart, we "wound up" the world lines of the static observers, which now appear as helices in the Born chart! Note too that, like the Langevin frame, the Born chart is only defined on the region 0 < r < 1/ω.
If we recompute the kinematic decomposition of the Langevin observers, that is of the timelike congruence
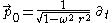 , we will of course obtain the same answer that we did before, only expressed in terms of the new chart. Specifically, the acceleration vector is
, we will of course obtain the same answer that we did before, only expressed in terms of the new chart. Specifically, the acceleration vector is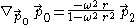
the expansion tensor vanishes, and the vorticity vector is


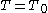 , the Langevin observers admit no such hyperslices. In particular, the spatial surfaces
, the Langevin observers admit no such hyperslices. In particular, the spatial surfaces 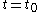 in the Born chart are orthogonal to the static observers, not to the Langevin observers. This is our second (and much more pointed) indication that defining "the spatial geometry of a rotating disk" is not as simple as one might expect.
in the Born chart are orthogonal to the static observers, not to the Langevin observers. This is our second (and much more pointed) indication that defining "the spatial geometry of a rotating disk" is not as simple as one might expect.To better understand this crucial point, consider integral curves of the third Langevin frame vector
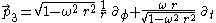
which pass through the radius
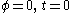 . (For convenience, we will suppress the inessential coordinate z from our discussion.) These curves lie in the surface
. (For convenience, we will suppress the inessential coordinate z from our discussion.) These curves lie in the surface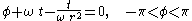
shown in the figure. We would like to regard this as a "space at a time" for our Langevin observers. But two things go wrong.
First, the Frobenius theorem tells us that
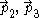 are tangent to no spatial hyperslice whatever. Indeed, except on the initial radius, the vectors
are tangent to no spatial hyperslice whatever. Indeed, except on the initial radius, the vectors 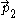 do not lie in our slice. Thus, while we found a spatial hypersurface, it is orthogonal to the world lines of only some our Langevin observers. Because the obstruction from the Frobenius theorem can be understood in terms of the failure of the vector fields
do not lie in our slice. Thus, while we found a spatial hypersurface, it is orthogonal to the world lines of only some our Langevin observers. Because the obstruction from the Frobenius theorem can be understood in terms of the failure of the vector fields 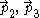 to form a Lie algebra
to form a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, this obstruction is differential, in fact Lie theoretic. That is, it is a kind of infinitesimal obstruction to the existence of a satisfactory notion of spatial hyperslices for our rotating observers.
Second, as the figure shows, our attempted hyperslice would lead to a discontinuous notion of "time" due to the "jumps" in the integral curves (shown as a coral colored discontinuity). Alternatively, we could try to use a multivalued time. Neither of these alternatives seems very attractive! This is evidently a global obstruction. It is of course a consequence of our inability to synchronize the clocks of the Langevin observers riding even a single ring---say the rim of a disk--- much less an entire disk.
The Sagnac effect
Imagine that we have fastened a fiber-optic cable around the circumference of a ring which is rotating with steady angular velocity ω. We wish to compute the round trip travel time, as measured by a ring-riding observer, for a laser pulse sent clockwise and counterclockwise around the cable. For simplicity, we will ignore the fact that light travels through a fiber optic cable at somewhat less than the speed of light in a vacuum, and will pretend that the world line of our laser pulse is a null curve (but certainly not a null geodesic!).In the Born line element, let us put
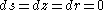 . This gives
. This gives
or

We obtain for the round trip travel time
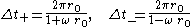
Putting
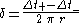 , we find
, we find  so that the ring-riding observers can determine the angular velocity of the ring (as measured by a static observer) from the difference between clockwise and counterclockwise travel times. This is known as the Sagnac effect
so that the ring-riding observers can determine the angular velocity of the ring (as measured by a static observer) from the difference between clockwise and counterclockwise travel times. This is known as the Sagnac effectSagnac effect
The Sagnac effect , named after French physicist Georges Sagnac, is a phenomenon encountered in interferometry that is elicited by rotation. The Sagnac effect manifests itself in a setup called ring interferometry. A beam of light is split and the two beams are made to follow a trajectory in...
. It is evidently a global effect.
Null Geodesics
We wish to compare the appearance of null geodesics in the cylindrical chart and the Born chart.In the cylindrical chart, the geodesic equations
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
read
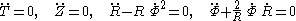
We immediately obtain the first integrals
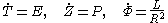
Plugging these into the expression obtained from the line element by setting
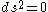 , we obtain
, we obtain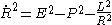
from which we see that the minimal radius of a null geodesic is given by
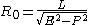
We can now solve to obtain the null geodesics as curves parameterized by an affine parameter, as follows:
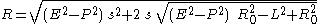
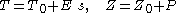

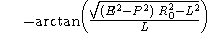
More useful for our purposes is the observation that the trajectory of a null geodesic (its projection into any spatial hyperslice
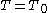 ) is of course a straight line, given by
) is of course a straight line, given by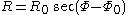
To obtain the minimal radius of the line through two points (on the same side of the point of closest approach to the origin), we solve
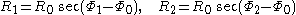
which gives
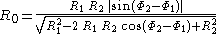

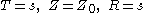
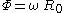
Transforming to the Born chart, we find that the trajectory can be written as
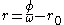
Similarly for inward bound radial null geodesics. The tracks turn out to appear slightly bent in the Born chart (see figure at right). (We will see in a later section that in the Born chart, we cannot properly refer to these "tracks" as "projections", however.)
Notice that, just as a duck hunter would expect, to send a laser pulse toward the stationary observer at R = 0, the Langevin obsevers have to aim slightly ahead to correct for their own motion. Turning things around, to send a laser pulse toward a Langevin observer riding a counterclockwise rotating ring, the central observer has to aim, not at this observer's current position, but at the position at which he will arrive just in time to intercept the signal. These families of inward and outward bound radial null geodesics represent very different curves in spacetime, but their projections do agree.

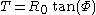
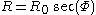
Transforming to Born coordinates, we obtain the equations
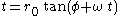
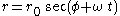
Eliminating φ gives
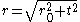
which shows that the geodesic does indeed appear to bend inward. We also find that
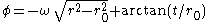
This completes the description of the appearance of null geodesics in the Born chart, since every null geodesic is either radial or else has some point of closest approach to the axis of cylindrical symmetry.
Note (see figure) that a ring-riding observer trying to send a laser pulse to another ring-riding observer must aim slightly ahead of his angular coordinate as given in the Born chart, in order to compensate for the rotational motion of the target. Note too that the picture presented here is fully compatible with our expectation (see appearance of the night sky) that a moving observer will see the apparent position of other objects on his celestial sphere to be displaced toward the direction of his motion.
Radar distance in the large

Rindler coordinates
In relativistic physics, the Rindler coordinate chart is an important and useful coordinate chart representing part of flat spacetime, also called the Minkowski vacuum. The Rindler chart was introduced by Wolfgang Rindler. The Rindler coordinate system or frame describes a uniformly accelerating...
) can employ various distinct but operationally significant notions of distance. Perhaps the simplest of these is radar distance.
Consider how a static observer at R=0 might determine his distance to a ring riding observer at R = R0. At event C he sends a radar pulse toward the ring, which strikes the world line of a ring-riding observer at A′ and then returns to the central observer at event C″. (See the right hand diagram in the figure at right.) He then divides the elapsed time (as measured by an ideal clock he carries) by two. It is not hard to see that he obtains for this distance simply R0 (in the cylindrical chart), or r0 (in the Born chart).
Similarly, a ring-riding observer can determine his distance to the central observer by sending a radar pulse, at event A toward the central observer, which strikes his world line at event C′ and returns to the ring-riding observer at event A″. (See the left hand diagram in the figure at right.) It is not hard to see that he obtains for this distance
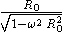 (in the cylindrical chart) or
(in the cylindrical chart) or 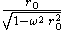 (in the Born chart), a result which is somewhat larger than the one obtained by the central observer. Thus, while radar distance has a simple operational significance, it is not even symmetric.
(in the Born chart), a result which is somewhat larger than the one obtained by the central observer. Thus, while radar distance has a simple operational significance, it is not even symmetric.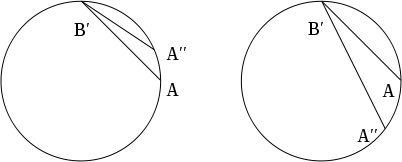
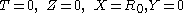
and we can write the coordinates of event B′ as
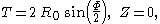
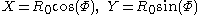
Writing the unknown elapsed proper time as
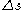 , we now write the coordinates of event A″ as
, we now write the coordinates of event A″ as
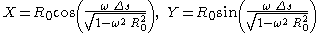
By requiring that the line segments connecting these events be null, we obtain an equation which in principle we can solve for Δ s. It turns out that this procedure gives a rather complicated nonlinear equation, so we simply present some representative numerical results. With R0 = 1, Φ = π/2, and ω = 1/10, we find that the radar distance from A to B is about 1.308, while the distance from B to A is about 1.505. As ω tends to zero, both results tend toward
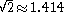 .
.Despite these possibly discouraging discrepancies, it is by no means impossible to devise a coordinate chart which is adapted to describing the physical experience of a single Langevin observer, or even a single arbitrarily accelerating observer in Minkowski spacetime. Pauri and Vallisneri have adapted the Märzke-Wheeler clock synchronization procedure to devise adapted coordinates they call Märzke-Wheeler coordinates (see the paper cited below). In the case of steady circular motion, this chart is in fact very closely related to the notion of radar distance "in the large" from a given Langevin observer.
Radar distance in the small
As was mentioned above, for various reasons the family of Langevin observers admits no family of orthogonal hyperslices. Therefore these observers simply cannot be associated with any slicing of spacetime into a family of successive "constant time slices".However, because the Langevin congruence is stationary, we can imagine replacing each world line in this congruence by a point. That is, we can consider the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of Minkowski spacetime (or rather, the region 0 < R < 1/ω) by the Langevin congruence, which is a three-dimensional topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
. Even better, we can place a Riemannian metric on this quotient manifold, turning it into a three dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, in such a way that the metric has a simple operational significance.
To see this, consider the Born line element
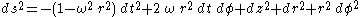

Setting ds2 = 0 and solving for dt we obtain
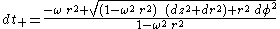
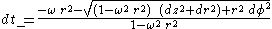
The elapsed proper time for a roundtrip radar blip emitted by a Langevin observer is then
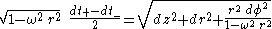
Therefore, in our quotient manifold, the Riemannian line element

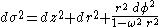
corresponds to distance between infinitesimally nearby Langevin observers. We will call it the Langevin-Landau-Lifschitz metric, and we can call this notion of distance radar distance "in the small".
This metric was first given by Langevin
Paul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
, but the interpretation in terms of radar distance "in the small" is due to Lev Landau
Lev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
and Evgeny Lifshitz
Evgeny Lifshitz
Evgeny Mikhailovich Lifshitz was a leading Soviet physicist of Jewish origin and the brother of physicist Ilya Mikhailovich Lifshitz. Lifshitz is well known in general relativity for coauthoring the BKL conjecture concerning the nature of a generic curvature...
, who generalized the construction to work for the quotient of any Lorentzian manifold by a stationary timelike congruence.
If we adopt the coframe
Frame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
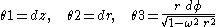
we can easily compute the Riemannian curvature tensor of our three dimensional quotient manifold. It has only one independent nontrivial component,
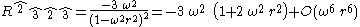
Thus, in some sense, the geometry of a rotating disk is curved, as Theodor Kaluza
Theodor Kaluza
Theodor Franz Eduard Kaluza was a German mathematician and physicist known for the Kaluza-Klein theory involving field equations in five-dimensional space...
claimed (without proof) as early as 1910. In fact, to fourth order in ω it has the geometry of the hyperbolic plane, just as Kaluza claimed.
Warning: as we have seen, there are many possible notions of distance which can be employed by Langevin observers riding on a rigidly rotating disk, so statements referring to "the geometry of a rotating disk" always require careful qualification.
To drive home this important point, let us use the Landau-Lifschitz metric to compute the distance between a Langevin observer riding a ring with radius R0 and a central static observer. To do this, we need only integrate our line element over the appropriate null geodesic track. From our earlier work, we see that we must plug
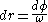
into our line element and integrate. This gives
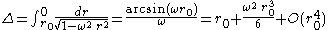
Because we are now dealing with a Riemannian metric, this notion of distance is of course symmetric under interchanging the two observers, unlike radar distance "in the large". The values given by this notion are intermediate between the radar distances computed in the previous section. For example, for r0 = 1, ω = 1/2, we find approximately Δ = 1.047, which can be compared with 1.155 for the distance from the ring-riding observer to the central observer, or 1 for the central observer to the ring-riding observer. Also, because up to second order the Landau-Lifschitz metric agrees with radar distance "in the large", we see that the curvature tensor we just computed does have operational significance: while radar distance "in the large" between pairs of Langevin observers is certainly not a Riemannian notion of distance, the distance between pairs of nearby Langevin observers does correspond to a Riemannian distance, given by the Langevin-Landau-Lifschitz metric. (In the felicitous phrase of Howard Percy Robertson
Howard Percy Robertson
Howard Percy Robertson was an American mathematician and physicist known for contributions related to physical cosmology and the uncertainty principle...
, this is kinematics im kleinem.)
One way to see that all reasonable notions of spatial distance for our Langevin observers agree for nearby observers is to show, following Nathan Rosen
Nathan Rosen
Nathan Rosen was an American-Israeli physicist noted for his study on the structure of the hydrogen molecule and his work with Albert Einstein and Boris Podolsky on entangled wave functions and the EPR paradox.-Background:Nathan Rosen was born into a Jewish family in Brooklyn, New York...
, that for any one Langevin observer, an instantaneously comoving inertial observer will also obtain the distances given by the Langevin-Landau-Lifschitz metric, for very small distances.
Summary
Observers riding on a rigidly rotating disk will conclude from measurements of small distances between themselves that the geometry of the disk is non-Euclidean. Regardless of which method they use, they will conclude that the geometry is well approximated by a certain Riemannian metric, namely the Langevin-Landau-Lifschitz metric. This is in turn very well approximated by the geometry of the hyperbolic plane (with the constant negative curvature -3 ω2). But if these observers measure larger distances, they will obtain different results, depending upon which method of measurement they use! In all such cases, however, they will most likely obtain results which are inconsistent with any Riemannian metric. In particular, if they use the simplest notion of distance, radar distance, owing to various effects such as the asymmetry already noted, they will conclude that the "geometry" of the disk is not only non-Euclidean, it is non-Riemannian.See also
- Ehrenfest paradoxEhrenfest paradoxThe Ehrenfest paradox concerns the rotation of a "rigid" disc in the theory of relativity.In its original formulation as presented by Paul Ehrenfest 1909 in the Physikalische Zeitschrift, it discusses an ideally rigid cylinder that is made to rotate about its axis of symmetry...
, for a sometimes controversial topic often studied using the Born chart. - Fibre optic gyroscopeFibre optic gyroscopeA fibre optic gyroscope senses changes in orientation, thus performing the function of a mechanical gyroscope. However its principle of operation is instead based on the interference of light which has passed through a coil of optical fibre which can be as long as 5 km.Two beams from a laser...
- Rindler coordinatesRindler coordinatesIn relativistic physics, the Rindler coordinate chart is an important and useful coordinate chart representing part of flat spacetime, also called the Minkowski vacuum. The Rindler chart was introduced by Wolfgang Rindler. The Rindler coordinate system or frame describes a uniformly accelerating...
, for another useful coordinate chart adapted to another important family of accelerated observers in Minkowski spacetime; this article also emphasizes the existence of distinct notions of distance which may be employed by such observers. - Sagnac effectSagnac effectThe Sagnac effect , named after French physicist Georges Sagnac, is a phenomenon encountered in interferometry that is elicited by rotation. The Sagnac effect manifests itself in a setup called ring interferometry. A beam of light is split and the two beams are made to follow a trajectory in...
External links
- The Rigid Rotating Disk in Relativity, by Michael Weiss (1995), from the sci.physics FAQ.

