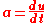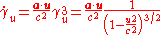Four-acceleration
Encyclopedia
In special relativity
, four-acceleration is a four-vector
and is defined as the change in four-velocity
over the particle's proper time
:
where
and
and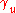 is the Lorentz factor
is the Lorentz factor
for the speed . A dot above a variable indicates a derivative with respect to the coordinate time in a given reference frame, not the proper time
. A dot above a variable indicates a derivative with respect to the coordinate time in a given reference frame, not the proper time  .
.
In an instantaneously co-moving inertial reference frame ,
,  and
and 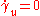 , i.e. in such a reference frame
, i.e. in such a reference frame
Geometrically, four-acceleration is a curvature vector of world line
.
Therefore, the magnitude of the four-acceleration (which is an invariant scalar) is equal to the proper acceleration
that a moving particle "feels" moving along a world line
.
The world lines having constant magnitude of four-acceleration are Minkowski-circles i.e. hyperbolas (see hyperbolic motion
)
The scalar product of a four-velocity
and the corresponding four-acceleration is always 0.
Even at relativistic speeds four-acceleration is related to the four-force such that
where m is the invariant mass
of a particle.
In general relativity
the elements of the acceleration four-vector are related to the elements of the four-velocity
through a covariant derivative
with respect to proper time.
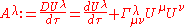
In special relativity the coordinates are those of a rectilinear inertial frame, so the Christoffel symbols
term vanishes, but sometimes when authors uses curved coordinates in order to describe an accelerated frame, the frame of reference isn't inertial, they will still describe the physics as special relativistic because the metric is just a frame transformation of the Minkowski space
metric. In that case this is the expression that must be used because the Christoffel symbols
are no longer all zero.
When the four-force is zero one has gravitation acting alone, and the four-vector version of Newton's second law above reduces to the geodesic equation.
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, four-acceleration is a four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
and is defined as the change in four-velocity
Four-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
over the particle's proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
:
-
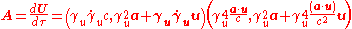 ,
,
where
and
and
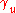 is the Lorentz factor
is the Lorentz factorLorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
for the speed
 . A dot above a variable indicates a derivative with respect to the coordinate time in a given reference frame, not the proper time
. A dot above a variable indicates a derivative with respect to the coordinate time in a given reference frame, not the proper time  .
.In an instantaneously co-moving inertial reference frame
 ,
,  and
and 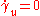 , i.e. in such a reference frame
, i.e. in such a reference frame
Geometrically, four-acceleration is a curvature vector of world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
.
Therefore, the magnitude of the four-acceleration (which is an invariant scalar) is equal to the proper acceleration
Proper acceleration
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
that a moving particle "feels" moving along a world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
.
The world lines having constant magnitude of four-acceleration are Minkowski-circles i.e. hyperbolas (see hyperbolic motion
Hyperbolic motion (relativity)
Hyperbolic motion is the motion of an object with constant proper acceleration in special relativity. It is called hyperbolic motion because the equation describing the path of the object through spacetime is a hyperbola, as can be seen when graphed on a Minkowski diagram.The proper acceleration...
)
The scalar product of a four-velocity
Four-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
and the corresponding four-acceleration is always 0.
Even at relativistic speeds four-acceleration is related to the four-force such that
where m is the invariant mass
Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
of a particle.
In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
the elements of the acceleration four-vector are related to the elements of the four-velocity
Four-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
through a covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
with respect to proper time.
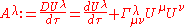
In special relativity the coordinates are those of a rectilinear inertial frame, so the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
term vanishes, but sometimes when authors uses curved coordinates in order to describe an accelerated frame, the frame of reference isn't inertial, they will still describe the physics as special relativistic because the metric is just a frame transformation of the Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
metric. In that case this is the expression that must be used because the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
are no longer all zero.
When the four-force is zero one has gravitation acting alone, and the four-vector version of Newton's second law above reduces to the geodesic equation.