
Rindler coordinates
Encyclopedia
In relativistic physics, the Rindler coordinate chart is an important and useful coordinate chart representing part of flat spacetime
, also called the Minkowski vacuum. The Rindler chart was introduced by Wolfgang Rindler
. The Rindler coordinate system or frame describes a uniformly accelerating frame of reference
in Minkowski space
. In special relativity
, a uniformly accelerating particle undergoes hyperbolic motion
. For each such particle a Rindler frame can be chosen in which it is at rest.
(an inertial frame) with the metric
In the region , which is often called the Rindler wedge, if g represents the proper acceleration (along the hyperbola x=1) of the Rindler observer whose proper time is defined to be equal to Rindler coordinate time (see below), the new chart is defined using the coordinate transformation
, which is often called the Rindler wedge, if g represents the proper acceleration (along the hyperbola x=1) of the Rindler observer whose proper time is defined to be equal to Rindler coordinate time (see below), the new chart is defined using the coordinate transformation
The inverse transformation is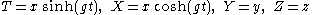
In the Rindler chart, the Minkowski line element
becomes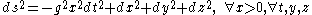
Any observer at rest in Rindler coordinates has constant proper acceleration
, with Rindler observers closer to the Rindler horizon having greater proper acceleration. All the Rindler observers are instantaneously at rest at time T=0 in the inertial frame, and at this time a Rindler observer with proper acceleration gi will be at position X = 1/gi (really X = c2/gi, but we assume units where c=1), which is also that observer's constant distance from the Rindler horizon in Rindler coordinates. If all Rindler observers set their clocks to zero at T=0, then when defining a Rindler coordinate system we have a choice of which Rindler observer's proper time
will be equal to the coordinate time t in Rindler coordinates, and this observer's proper acceleration defines the value of g above (for other Rindler observers at different distances from the Rindler horizon, the coordinate time will equal some constant multiple of their own proper time). It is a common convention to define the Rindler coordinate system so that the Rindler observer whose proper time matches coordinate time is the one who has proper acceleration g=1, so that g can be eliminated from the equations
The above equation,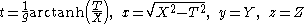
has been simplified for c=1. The unsimplified equation is more convenient for finding the Rindler Horizon distance, given an acceleration g.

The remainder of the article will follow the convention of setting both g=1 and c=1, so units for X and x will be 1 unit = c^2/g = 1. Be mindful that setting g=1 light-second/second2 is very different from setting g=1 light-year/year^2. Even if we pick units where c=1, the magnitude of the proper acceleration g will depend on our choice of units: for example, if we use units of light-years for distance, (X or x) and years for time, (T or t), this would mean g = 1 light year/year2, equal to about 9.5 meters/second2, while if we use units of light-seconds for distance, (X or x), and seconds for time, (T or t), this would mean g = 1 light-second/second2, or 299792458 meters/second2).

which has the dual frame field
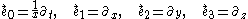
This defines a local Lorentz frame in the tangent space
at each event (in the region covered by our Rindler chart, namely the Rindler wedge). The integral curve
s of the timelike unit vector field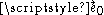 give a timelike congruence
give a timelike congruence
, consisting of the world lines of a family of observers called the Rindler observers. In the Rindler chart, these world lines appear as the vertical coordinate lines . Using the coordinate transformation above, we find that these correspond to hyperbolic arcs in the original Cartesian chart.
. Using the coordinate transformation above, we find that these correspond to hyperbolic arcs in the original Cartesian chart.
As with any timelike congruence in any Lorentzian manifold, this congruence has a kinematic decomposition (see Raychaudhuri equation
). In this case, the expansion and vorticity of the congruence of Rindler observers vanish. The vanishing of the expansion tensor implies that each of our observers maintains constant distance to his neighbors. The vanishing of the vorticity tensor implies that the world lines of our observers are not twisting about each other; this is a kind of local absence of "swirling".
The acceleration vector
of each observer is given by the covariant derivative
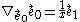
That is, each Rindler observer is accelerating in the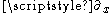 direction. Individually speaking, each observer is in fact accelerating with constant magnitude in this direction, so their world lines are the Lorentzian analogs of circles, which are the curves of constant path curvature in the Euclidean geometry.
direction. Individually speaking, each observer is in fact accelerating with constant magnitude in this direction, so their world lines are the Lorentzian analogs of circles, which are the curves of constant path curvature in the Euclidean geometry.
Because the Rindler observers are vorticity-free, they are also hypersurface orthogonal. The orthogonal spatial hyperslices are ; these appear as horizontal half-planes in the Rindler chart and as half-planes through
; these appear as horizontal half-planes in the Rindler chart and as half-planes through 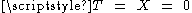 in the Cartesian chart (see the figure above). Setting
in the Cartesian chart (see the figure above). Setting 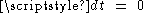 in the line element, we see that these have the ordinary Euclidean geometry,
in the line element, we see that these have the ordinary Euclidean geometry, 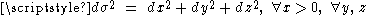 . Thus, the spatial coordinates in the Rindler chart have a very simple interpretation consistent with the claim that the Rindler observers are mutually stationary. We will return to this rigidity property of the Rindler observers a bit later in this article.
. Thus, the spatial coordinates in the Rindler chart have a very simple interpretation consistent with the claim that the Rindler observers are mutually stationary. We will return to this rigidity property of the Rindler observers a bit later in this article.
This phenomenon is the basis of a well known "paradox", Bell's spaceship paradox
. However, it is a simple consequence of relativistic kinematics. One way to see this is to observe that the magnitude of the acceleration vector is just the path curvature
of the corresponding world line. But the world lines of our Rindler observers are the analogs of a family of concentric circles in the Euclidean plane, so we are simply dealing with the Lorentzian analog of a fact familiar to speed skaters: in a family of concentric circles, inner circles must bend faster (per unit arc length) than the outer ones.

Transforming these vector fields using the coordinate transformation given above, we find that in the Rindler chart (in the Rinder wedge) this frame becomes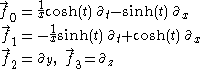
Computing the kinematic decomposition of the timelike congruence defined by the timelike unit vector field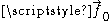 , we find that the expansion and vorticity again vanishes, and in addition the acceleration vector vanishes,
, we find that the expansion and vorticity again vanishes, and in addition the acceleration vector vanishes, 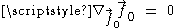 . In other words, this is a geodesic congruence; the corresponding observers are in a state of inertial motion. In the original Cartesian chart, these observers, whom we will call Minkowski observers, are at rest.
. In other words, this is a geodesic congruence; the corresponding observers are in a state of inertial motion. In the original Cartesian chart, these observers, whom we will call Minkowski observers, are at rest.
In the Rindler chart, the world lines of the Minkowski observers appear as hyperbolic secant curves asymptotic to the coordinate plane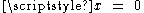 . Specifically, in Rindler coordinates, the world line of the Minkowski observer passing through the event
. Specifically, in Rindler coordinates, the world line of the Minkowski observer passing through the event  is
is
where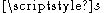 is the proper time of this Minkowski observer. Note that only a small portion of his history is covered by the Rindler chart! This shows explicitly why the Rindler chart is not geodesically complete; timelike geodesics run outside the region covered by the chart in finite proper time. Of course, we already knew that the Rindler chart cannot be geodesically complete, because it covers only a portion of the original Cartesian chart, which is a geodesically complete chart.
is the proper time of this Minkowski observer. Note that only a small portion of his history is covered by the Rindler chart! This shows explicitly why the Rindler chart is not geodesically complete; timelike geodesics run outside the region covered by the chart in finite proper time. Of course, we already knew that the Rindler chart cannot be geodesically complete, because it covers only a portion of the original Cartesian chart, which is a geodesically complete chart.
In the case depicted in the figure, and we have drawn (correctly scaled and boosted) the light cones at
and we have drawn (correctly scaled and boosted) the light cones at 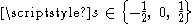 .
.
. This happens because as x → 0 the acceleration of the Rindler observers diverges. As we can see from the figure illustrating the Rindler wedge, the locus x = 0 in the Rindler chart corresponds to the locus T2 = X2, X > 0 in the Cartesian chart, which consists of two null half-planes, each ruled by a null geodesic congruence.
For the moment, we simply consider the Rindler horizon as the boundary of the Rindler coordinates. If we consider the set of accelerating observers who have a constant position in Rindler coordinates, none of them can ever receive light signals from events with T ≥ X (on the diagram, these would be events on or to the left of the line T = X which the upper red horizon lies along; these observers could however receive signals from events with T ≥ X if they stopped their acceleration and crossed this line themselves) nor can they ever send signals to events with T ≤ −X (events on or to the left of the line T = −X which the lower red horizon lies along; in this case the acceleration is actually irrelevant, no observer to the right of this line can send a signal to events with T ≤ −X simply because those events lie outside their own future light cone
). Also, if we consider members of this set of accelerating observers closer and closer to the horizon, in the limit as the distance to the horizon approaches zero, the constant proper acceleration experienced by an observer at this distance (which would also be the G-force experienced by such an observer) would approach infinity. Both of these facts would also be true if we were considering a set of observers hovering outside the event horizon
of a black hole
, each observer hovering at a constant radius in Schwarzschild coordinates
. In fact, in the close neighborhood of a black hole, the geometry close to the event horizon can be described in Rindler coordinates. Hawking radiation in the case of an accelerating frame is referred to as Unruh radiation. The connection is the equivalence of acceleration with gravitation.
; they are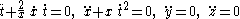
Of course, in the original Cartesian chart, the geodesics appear as straight lines, so we could easily obtain them in the Rindler chart using our coordinate transformation. However, it is instructive to obtain and study them independently of the original chart, and we shall do so in this section.
From the first, third, and fourth we immediately obtain the first integrals
But from the line element we have where
where 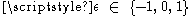 for timelike, null, and spacelike geodesics, respectively. This gives the fourth first integral, namely
for timelike, null, and spacelike geodesics, respectively. This gives the fourth first integral, namely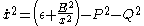 .
.
This suffices to give the complete solution of the geodesic equations.
In the case of null geodesics, from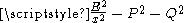 with nonzero
with nonzero 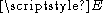 , we see that the x coordinate ranges over the interval
, we see that the x coordinate ranges over the interval 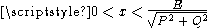 .
.
The complete seven parameter family giving any null geodesic through any event in the Rindler wedge, is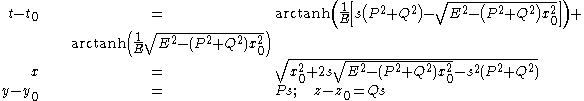
Plotting the tracks of some representative null geodesics through a given event (that is, projecting to the hyperslice ), we obtain a picture which looks suspiciously like the family of all semicircles through a point and orthogonal to the Rindler horizon! (See the figure.)
), we obtain a picture which looks suspiciously like the family of all semicircles through a point and orthogonal to the Rindler horizon! (See the figure.)
is one in which a vorticity-free timelike Killing vector field can be found. In this case, we have a uniquely defined family of (identical) spatial hyperslices orthogonal to the corresponding static observers (who need not be inertial observers). This allows us to define a new metric on any of these hyperslices which is conformally related to the original metric inherited from the spacetime, but with the property that geodesics in the new metric (note this is a Riemannian metric on a Riemannian three-manifold) are precisely the projections of the null geodesics of spacetime. This new metric is called the Fermat metric, and in a static spacetime endowed with a coordinate chart in which the line element has the form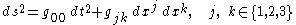
the Fermat metric on is simply
is simply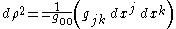
(where the metric coeffients are understood to be evaluated at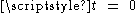 ).
).
In the Rindler chart, the timelike translation is such a Killing vector field, so this is a static spacetime (not surprisingly, since Minkowski spacetime is of course trivially a static vacuum solution of the Einstein field equation). Therefore, we may immediately write down the Fermat metric for the Rindler observers:
is such a Killing vector field, so this is a static spacetime (not surprisingly, since Minkowski spacetime is of course trivially a static vacuum solution of the Einstein field equation). Therefore, we may immediately write down the Fermat metric for the Rindler observers: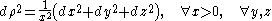
But this is the well-known line element of hyperbolic three-space H3 in the upper half space chart! This is closely analogous to the well known upper half plane chart for the hyperbolic plane H2, which is familiar to generations of complex analysis
students in connection with conformal mapping problems (and much more), and many mathematically minded readers already know that the geodesics of H2 in the upper half plane model are simply semicircles (orthogonal to the circle at infinity represented by the real axis).
However, it is instructive to write down and solve the Killing vector equations directly. We obtain four familiar looking Killing vector fields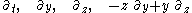
(time translation, spatial translations orthogonal to the direction of acceleration, and spatial rotation orthogonal to the direction of acceleration) plus six more: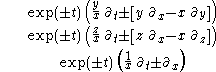
(where the signs are chosen consistently + or −). We leave it as an exercise to figure out how these are related to the standard generators; here we wish to point out that we must be able to obtain generators equivalent to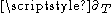 in the Cartesian chart, yet the Rindler wedge is obviously not invariant under this translation. How can this be? The answer is that like anything defined by a system of partial differential equations on a smooth manifold, the Killing equation will in general have locally defined solutions, but these might not exist globally. That is, with suitable restrictions on the group parameter, a Killing flow can always be defined in a suitable local neighborhood, but the flow might not be well-defined globally. This has nothing to do with Lorentzian manifolds per se, since the same issue arises in the study of general smooth manifolds.
in the Cartesian chart, yet the Rindler wedge is obviously not invariant under this translation. How can this be? The answer is that like anything defined by a system of partial differential equations on a smooth manifold, the Killing equation will in general have locally defined solutions, but these might not exist globally. That is, with suitable restrictions on the group parameter, a Killing flow can always be defined in a suitable local neighborhood, but the flow might not be well-defined globally. This has nothing to do with Lorentzian manifolds per se, since the same issue arises in the study of general smooth manifolds.
which can be used by the Rindler observers.
The first is the one we have tacitly employed above: the induced Riemannian metric on the spatial hyperslices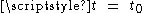 . We will call this the ruler distance since it corresponds to this induced Riemannian metric, but its operational meaning might not be immediately apparent.
. We will call this the ruler distance since it corresponds to this induced Riemannian metric, but its operational meaning might not be immediately apparent.
From the standpoint of physical measurement, a more natural notion of distance between two world lines is the radar distance. This is computed by sending a null geodesic from the world line of our observer (event A) to the world line of some small object, whereupon it is reflected (event B) and returns to the observer (event C). The radar distance is then obtained by dividing the round trip travel time, as measured by an ideal clock carried by our observer.
(In Minkowski spacetime, fortunately, we can ignore the possibility of multiple null geodesic paths between two world lines, but in cosmological models and other applications things are not so simple! We should also caution against assuming that this notion of distance between two observers gives a notion which is symmetric under interchanging the observers!)
In particular, let us consider a pair of Rindler observers with coordinates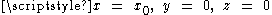 and
and  respectively. (Note that the first of these, the trailing observer, is accelerating a bit harder, in order to keep up with the leading observer). Setting
respectively. (Note that the first of these, the trailing observer, is accelerating a bit harder, in order to keep up with the leading observer). Setting 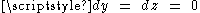 in the Rindler line element, we readily obtain the equation of null geodesics moving in the direction of acceleration:
in the Rindler line element, we readily obtain the equation of null geodesics moving in the direction of acceleration: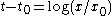
Therefore, the radar distance between these two observers is given by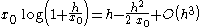
This is a bit smaller than the ruler distance, but for nearby observers the discrepancy is negligible.
A third possible notion of distance is this: our observer measures the angle subtended by a unit disk placed on some object (not a point object!), as it appears from his location. We call this the optical diameter distance. Because of the simple character of null geodesics in Minkowski spacetime, we can readily determine the optical distance between our pair of Rindler observers (aligned with the direction of acceleration). From a sketch it should be plausible that the optical diameter distance scales like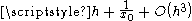 . Therefore, in the case of a trailing observer estimating distance to a leading observer (the case
. Therefore, in the case of a trailing observer estimating distance to a leading observer (the case 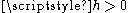 ), the optical distance is a bit larger than the ruler distance, which is a bit larger than the radar distance. The reader should now take a moment to consider the case of a leading observer estimating distance to a trailing observer!
), the optical distance is a bit larger than the ruler distance, which is a bit larger than the radar distance. The reader should now take a moment to consider the case of a leading observer estimating distance to a trailing observer!
There are other notions of distance, but the main point is clear: while the values of these various notions will in general disagree for a given pair of Rindler observers, they all agree that every pair of Rindler observers maintains constant distance. The fact that very nearby Rindler observers are mutually stationary follows from the fact, noted above, that the expansion tensor of the Rindler congruence vanishes identically. However, we have shown here that in various senses, this rigidity property holds at larger scales. This is truly a remarkable rigidity property, given the well-known fact that in relativistic physics, no rod can be accelerated rigidly (and no disk can be spun up rigidly) — at least, not without sustaining inhomogeneous stresses. The easiest way to see this is to observe that in Newtonian physics, if we "kick" a rigid body, all elements of matter in the body will immediately change their state of motion. This is of course incompatible with the relativistic principle that no information having any physical effect can be transmitted faster than the speed of light.
It follows that if a rod is accelerated by some external force applied anywhere along its length, the elements of matter in various different places in the rod cannot all feel the same magnitude of acceleration if the rod is not to extend without bound and ultimately break. In other words, an accelerated rod which does not break must sustain stresses which vary along its length. Furthermore, in any thought experiment with time varying forces, whether we "kick" an object or try to accelerate it gradually, we cannot avoid the problem of avoiding mechanical models which are inconsistent with relativistic kinematics (because distant parts of the body respond too quickly to an applied force).
Returning to the question of the operational significance of the ruler distance, we see that this should be the distance which our observers will obtain should they very slowly pass from hand to hand a small ruler which is repeatedly set end to end. But justifying this interpretation in detail would require some kind of material model.
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, also called the Minkowski vacuum. The Rindler chart was introduced by Wolfgang Rindler
Wolfgang Rindler
Wolfgang Rindler is a leading physicist working in the field of General Relativity where he is well known for introducing the term "event horizon", Rindler coordinates, and for popularizing the use of spinors in general relativity. He is also a prolific textbook author.-Education:Rindler gained...
. The Rindler coordinate system or frame describes a uniformly accelerating frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. In special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, a uniformly accelerating particle undergoes hyperbolic motion
Hyperbolic motion (relativity)
Hyperbolic motion is the motion of an object with constant proper acceleration in special relativity. It is called hyperbolic motion because the equation describing the path of the object through spacetime is a hyperbola, as can be seen when graphed on a Minkowski diagram.The proper acceleration...
. For each such particle a Rindler frame can be chosen in which it is at rest.
Relation to Cartesian chart
To obtain the Rindler chart, start with the Cartesian chartCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
(an inertial frame) with the metric

In the region
 , which is often called the Rindler wedge, if g represents the proper acceleration (along the hyperbola x=1) of the Rindler observer whose proper time is defined to be equal to Rindler coordinate time (see below), the new chart is defined using the coordinate transformation
, which is often called the Rindler wedge, if g represents the proper acceleration (along the hyperbola x=1) of the Rindler observer whose proper time is defined to be equal to Rindler coordinate time (see below), the new chart is defined using the coordinate transformation
The inverse transformation is
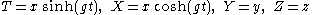
In the Rindler chart, the Minkowski line element
Line element
A line element ds in mathematics can most generally be thought of as the change in a position vector in an affine space expressing the change of the arc length. An easy way of visualizing this relationship is by parametrizing the given curve by Frenet–Serret formulas...
becomes
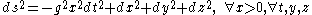
Any observer at rest in Rindler coordinates has constant proper acceleration
Proper acceleration
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
, with Rindler observers closer to the Rindler horizon having greater proper acceleration. All the Rindler observers are instantaneously at rest at time T=0 in the inertial frame, and at this time a Rindler observer with proper acceleration gi will be at position X = 1/gi (really X = c2/gi, but we assume units where c=1), which is also that observer's constant distance from the Rindler horizon in Rindler coordinates. If all Rindler observers set their clocks to zero at T=0, then when defining a Rindler coordinate system we have a choice of which Rindler observer's proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
will be equal to the coordinate time t in Rindler coordinates, and this observer's proper acceleration defines the value of g above (for other Rindler observers at different distances from the Rindler horizon, the coordinate time will equal some constant multiple of their own proper time). It is a common convention to define the Rindler coordinate system so that the Rindler observer whose proper time matches coordinate time is the one who has proper acceleration g=1, so that g can be eliminated from the equations
The above equation,
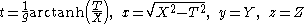
has been simplified for c=1. The unsimplified equation is more convenient for finding the Rindler Horizon distance, given an acceleration g.

The remainder of the article will follow the convention of setting both g=1 and c=1, so units for X and x will be 1 unit = c^2/g = 1. Be mindful that setting g=1 light-second/second2 is very different from setting g=1 light-year/year^2. Even if we pick units where c=1, the magnitude of the proper acceleration g will depend on our choice of units: for example, if we use units of light-years for distance, (X or x) and years for time, (T or t), this would mean g = 1 light year/year2, equal to about 9.5 meters/second2, while if we use units of light-seconds for distance, (X or x), and seconds for time, (T or t), this would mean g = 1 light-second/second2, or 299792458 meters/second2).
The Rindler observers
In the new chart, it is natural to take the coframe field
which has the dual frame field
Frame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
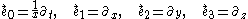
This defines a local Lorentz frame in the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at each event (in the region covered by our Rindler chart, namely the Rindler wedge). The integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s of the timelike unit vector field
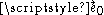 give a timelike congruence
give a timelike congruenceCongruence (general relativity)
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
, consisting of the world lines of a family of observers called the Rindler observers. In the Rindler chart, these world lines appear as the vertical coordinate lines
 . Using the coordinate transformation above, we find that these correspond to hyperbolic arcs in the original Cartesian chart.
. Using the coordinate transformation above, we find that these correspond to hyperbolic arcs in the original Cartesian chart.As with any timelike congruence in any Lorentzian manifold, this congruence has a kinematic decomposition (see Raychaudhuri equation
Raychaudhuri equation
In general relativity, the Raychaudhuri equation, or Landau-Raychaudhuri equation, is a fundamental result describing the motion of nearby bits of matter....
). In this case, the expansion and vorticity of the congruence of Rindler observers vanish. The vanishing of the expansion tensor implies that each of our observers maintains constant distance to his neighbors. The vanishing of the vorticity tensor implies that the world lines of our observers are not twisting about each other; this is a kind of local absence of "swirling".
The acceleration vector
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
of each observer is given by the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
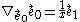
That is, each Rindler observer is accelerating in the
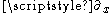 direction. Individually speaking, each observer is in fact accelerating with constant magnitude in this direction, so their world lines are the Lorentzian analogs of circles, which are the curves of constant path curvature in the Euclidean geometry.
direction. Individually speaking, each observer is in fact accelerating with constant magnitude in this direction, so their world lines are the Lorentzian analogs of circles, which are the curves of constant path curvature in the Euclidean geometry.Because the Rindler observers are vorticity-free, they are also hypersurface orthogonal. The orthogonal spatial hyperslices are
 ; these appear as horizontal half-planes in the Rindler chart and as half-planes through
; these appear as horizontal half-planes in the Rindler chart and as half-planes through 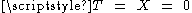 in the Cartesian chart (see the figure above). Setting
in the Cartesian chart (see the figure above). Setting 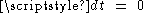 in the line element, we see that these have the ordinary Euclidean geometry,
in the line element, we see that these have the ordinary Euclidean geometry, 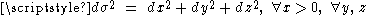 . Thus, the spatial coordinates in the Rindler chart have a very simple interpretation consistent with the claim that the Rindler observers are mutually stationary. We will return to this rigidity property of the Rindler observers a bit later in this article.
. Thus, the spatial coordinates in the Rindler chart have a very simple interpretation consistent with the claim that the Rindler observers are mutually stationary. We will return to this rigidity property of the Rindler observers a bit later in this article.A "paradoxical" property
Note that Rindler observers with smaller constant x coordinate are accelerating harder to keep up! This may seem surprising because in Newtonian physics, observers who maintain constant relative distance must share the same acceleration. But in relativistic physics, we see that the trailing endpoint of a rod which is accelerated by some external force (parallel to its symmetry axis) must accelerate a bit harder than the leading endpoint, or else it must ultimately break. This is a manifestation of Lorentz contraction. As the rod accelerates its velocity increases and its length decreases. Since it is getting shorter, the back end must accelerate harder than the front. Another way to look at it is: the backend must achieve the same change in velocity in a shorter period of time. This leads to a differential equation showing, that at some distance, the acceleration of the trailing end diverges, resulting in the Rindler horizon.This phenomenon is the basis of a well known "paradox", Bell's spaceship paradox
Bell's spaceship paradox
Bell's spaceship paradox is a thought experiment in special relativity involving accelerated spaceships and strings. The results of this thought experiment are for many people paradoxical. While J. S. Bell's 1976 version of the paradox is the most widely known, it was first designed by E. Dewan and M...
. However, it is a simple consequence of relativistic kinematics. One way to see this is to observe that the magnitude of the acceleration vector is just the path curvature
Geodesic curvature
In Riemannian geometry, the geodesic curvature k_g of a curve lying on a submanifold of the ambient space measures how far the curve is from being a geodesic...
of the corresponding world line. But the world lines of our Rindler observers are the analogs of a family of concentric circles in the Euclidean plane, so we are simply dealing with the Lorentzian analog of a fact familiar to speed skaters: in a family of concentric circles, inner circles must bend faster (per unit arc length) than the outer ones.
Minkowski observers
It is worthwhile to also introduce an alternative frame, given in the Minkowski chart by the natural choice
Transforming these vector fields using the coordinate transformation given above, we find that in the Rindler chart (in the Rinder wedge) this frame becomes
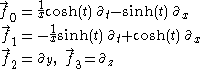
Computing the kinematic decomposition of the timelike congruence defined by the timelike unit vector field
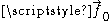 , we find that the expansion and vorticity again vanishes, and in addition the acceleration vector vanishes,
, we find that the expansion and vorticity again vanishes, and in addition the acceleration vector vanishes, 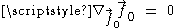 . In other words, this is a geodesic congruence; the corresponding observers are in a state of inertial motion. In the original Cartesian chart, these observers, whom we will call Minkowski observers, are at rest.
. In other words, this is a geodesic congruence; the corresponding observers are in a state of inertial motion. In the original Cartesian chart, these observers, whom we will call Minkowski observers, are at rest.In the Rindler chart, the world lines of the Minkowski observers appear as hyperbolic secant curves asymptotic to the coordinate plane
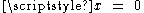 . Specifically, in Rindler coordinates, the world line of the Minkowski observer passing through the event
. Specifically, in Rindler coordinates, the world line of the Minkowski observer passing through the event  is
is
where
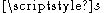 is the proper time of this Minkowski observer. Note that only a small portion of his history is covered by the Rindler chart! This shows explicitly why the Rindler chart is not geodesically complete; timelike geodesics run outside the region covered by the chart in finite proper time. Of course, we already knew that the Rindler chart cannot be geodesically complete, because it covers only a portion of the original Cartesian chart, which is a geodesically complete chart.
is the proper time of this Minkowski observer. Note that only a small portion of his history is covered by the Rindler chart! This shows explicitly why the Rindler chart is not geodesically complete; timelike geodesics run outside the region covered by the chart in finite proper time. Of course, we already knew that the Rindler chart cannot be geodesically complete, because it covers only a portion of the original Cartesian chart, which is a geodesically complete chart.In the case depicted in the figure,
 and we have drawn (correctly scaled and boosted) the light cones at
and we have drawn (correctly scaled and boosted) the light cones at 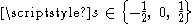 .
.The Rindler horizon
The Rindler coordinate chart has a coordinate singularity at x = 0, where the metric tensor (expressed in the Rindler coordinates) has vanishing determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. This happens because as x → 0 the acceleration of the Rindler observers diverges. As we can see from the figure illustrating the Rindler wedge, the locus x = 0 in the Rindler chart corresponds to the locus T2 = X2, X > 0 in the Cartesian chart, which consists of two null half-planes, each ruled by a null geodesic congruence.
For the moment, we simply consider the Rindler horizon as the boundary of the Rindler coordinates. If we consider the set of accelerating observers who have a constant position in Rindler coordinates, none of them can ever receive light signals from events with T ≥ X (on the diagram, these would be events on or to the left of the line T = X which the upper red horizon lies along; these observers could however receive signals from events with T ≥ X if they stopped their acceleration and crossed this line themselves) nor can they ever send signals to events with T ≤ −X (events on or to the left of the line T = −X which the lower red horizon lies along; in this case the acceleration is actually irrelevant, no observer to the right of this line can send a signal to events with T ≤ −X simply because those events lie outside their own future light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
). Also, if we consider members of this set of accelerating observers closer and closer to the horizon, in the limit as the distance to the horizon approaches zero, the constant proper acceleration experienced by an observer at this distance (which would also be the G-force experienced by such an observer) would approach infinity. Both of these facts would also be true if we were considering a set of observers hovering outside the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
of a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
, each observer hovering at a constant radius in Schwarzschild coordinates
Schwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
. In fact, in the close neighborhood of a black hole, the geometry close to the event horizon can be described in Rindler coordinates. Hawking radiation in the case of an accelerating frame is referred to as Unruh radiation. The connection is the equivalence of acceleration with gravitation.
Geodesics
The geodesic equations in the Rindler chart are easily obtained from the geodesic LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
; they are
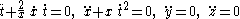
Of course, in the original Cartesian chart, the geodesics appear as straight lines, so we could easily obtain them in the Rindler chart using our coordinate transformation. However, it is instructive to obtain and study them independently of the original chart, and we shall do so in this section.
From the first, third, and fourth we immediately obtain the first integrals

But from the line element we have
 where
where 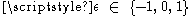 for timelike, null, and spacelike geodesics, respectively. This gives the fourth first integral, namely
for timelike, null, and spacelike geodesics, respectively. This gives the fourth first integral, namely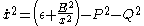 .
.This suffices to give the complete solution of the geodesic equations.
In the case of null geodesics, from
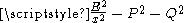 with nonzero
with nonzero 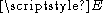 , we see that the x coordinate ranges over the interval
, we see that the x coordinate ranges over the interval 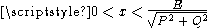 .
.The complete seven parameter family giving any null geodesic through any event in the Rindler wedge, is
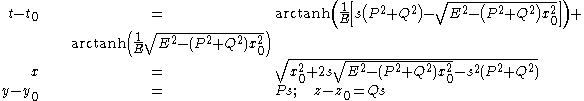
Plotting the tracks of some representative null geodesics through a given event (that is, projecting to the hyperslice
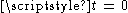 ), we obtain a picture which looks suspiciously like the family of all semicircles through a point and orthogonal to the Rindler horizon! (See the figure.)
), we obtain a picture which looks suspiciously like the family of all semicircles through a point and orthogonal to the Rindler horizon! (See the figure.)The Fermat metric
The fact that in the Rindler chart, the projections of null geodesics into any spatial hyperslice for the Rindler observers are simply semicircular arcs can be verified directly from the general solution just given, but there is a very simple way to see this. A static spacetimeStatic spacetime
In general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...
is one in which a vorticity-free timelike Killing vector field can be found. In this case, we have a uniquely defined family of (identical) spatial hyperslices orthogonal to the corresponding static observers (who need not be inertial observers). This allows us to define a new metric on any of these hyperslices which is conformally related to the original metric inherited from the spacetime, but with the property that geodesics in the new metric (note this is a Riemannian metric on a Riemannian three-manifold) are precisely the projections of the null geodesics of spacetime. This new metric is called the Fermat metric, and in a static spacetime endowed with a coordinate chart in which the line element has the form
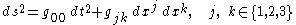
the Fermat metric on
 is simply
is simply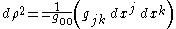
(where the metric coeffients are understood to be evaluated at
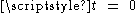 ).
).In the Rindler chart, the timelike translation
 is such a Killing vector field, so this is a static spacetime (not surprisingly, since Minkowski spacetime is of course trivially a static vacuum solution of the Einstein field equation). Therefore, we may immediately write down the Fermat metric for the Rindler observers:
is such a Killing vector field, so this is a static spacetime (not surprisingly, since Minkowski spacetime is of course trivially a static vacuum solution of the Einstein field equation). Therefore, we may immediately write down the Fermat metric for the Rindler observers: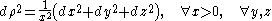
But this is the well-known line element of hyperbolic three-space H3 in the upper half space chart! This is closely analogous to the well known upper half plane chart for the hyperbolic plane H2, which is familiar to generations of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
students in connection with conformal mapping problems (and much more), and many mathematically minded readers already know that the geodesics of H2 in the upper half plane model are simply semicircles (orthogonal to the circle at infinity represented by the real axis).
Symmetries
Since the Rindler chart is a coordinate chart for Minkowski spacetime, we expect to find ten linearly independent Killing vector fields. Indeed, in the Cartesian chart we can readily find ten linearly independent Killing vector fields, generating respectively one parameter subgroups of time translation, three spatials, three rotations and three boosts. Together these generate the (proper isochronous) Poincaré group, the symmetry group of Minkowski spacetime.However, it is instructive to write down and solve the Killing vector equations directly. We obtain four familiar looking Killing vector fields
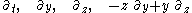
(time translation, spatial translations orthogonal to the direction of acceleration, and spatial rotation orthogonal to the direction of acceleration) plus six more:
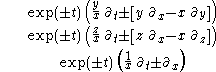
(where the signs are chosen consistently + or −). We leave it as an exercise to figure out how these are related to the standard generators; here we wish to point out that we must be able to obtain generators equivalent to
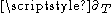 in the Cartesian chart, yet the Rindler wedge is obviously not invariant under this translation. How can this be? The answer is that like anything defined by a system of partial differential equations on a smooth manifold, the Killing equation will in general have locally defined solutions, but these might not exist globally. That is, with suitable restrictions on the group parameter, a Killing flow can always be defined in a suitable local neighborhood, but the flow might not be well-defined globally. This has nothing to do with Lorentzian manifolds per se, since the same issue arises in the study of general smooth manifolds.
in the Cartesian chart, yet the Rindler wedge is obviously not invariant under this translation. How can this be? The answer is that like anything defined by a system of partial differential equations on a smooth manifold, the Killing equation will in general have locally defined solutions, but these might not exist globally. That is, with suitable restrictions on the group parameter, a Killing flow can always be defined in a suitable local neighborhood, but the flow might not be well-defined globally. This has nothing to do with Lorentzian manifolds per se, since the same issue arises in the study of general smooth manifolds.Notions of distance
One of the many valuable lessons to be learned from a study of the Rindler chart is that there are in fact several distinct (but reasonable) notions of distanceDistance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
which can be used by the Rindler observers.
The first is the one we have tacitly employed above: the induced Riemannian metric on the spatial hyperslices
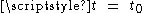 . We will call this the ruler distance since it corresponds to this induced Riemannian metric, but its operational meaning might not be immediately apparent.
. We will call this the ruler distance since it corresponds to this induced Riemannian metric, but its operational meaning might not be immediately apparent.From the standpoint of physical measurement, a more natural notion of distance between two world lines is the radar distance. This is computed by sending a null geodesic from the world line of our observer (event A) to the world line of some small object, whereupon it is reflected (event B) and returns to the observer (event C). The radar distance is then obtained by dividing the round trip travel time, as measured by an ideal clock carried by our observer.
(In Minkowski spacetime, fortunately, we can ignore the possibility of multiple null geodesic paths between two world lines, but in cosmological models and other applications things are not so simple! We should also caution against assuming that this notion of distance between two observers gives a notion which is symmetric under interchanging the observers!)
In particular, let us consider a pair of Rindler observers with coordinates
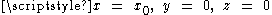 and
and  respectively. (Note that the first of these, the trailing observer, is accelerating a bit harder, in order to keep up with the leading observer). Setting
respectively. (Note that the first of these, the trailing observer, is accelerating a bit harder, in order to keep up with the leading observer). Setting 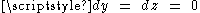 in the Rindler line element, we readily obtain the equation of null geodesics moving in the direction of acceleration:
in the Rindler line element, we readily obtain the equation of null geodesics moving in the direction of acceleration: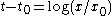
Therefore, the radar distance between these two observers is given by
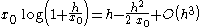
This is a bit smaller than the ruler distance, but for nearby observers the discrepancy is negligible.
A third possible notion of distance is this: our observer measures the angle subtended by a unit disk placed on some object (not a point object!), as it appears from his location. We call this the optical diameter distance. Because of the simple character of null geodesics in Minkowski spacetime, we can readily determine the optical distance between our pair of Rindler observers (aligned with the direction of acceleration). From a sketch it should be plausible that the optical diameter distance scales like
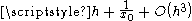 . Therefore, in the case of a trailing observer estimating distance to a leading observer (the case
. Therefore, in the case of a trailing observer estimating distance to a leading observer (the case 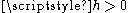 ), the optical distance is a bit larger than the ruler distance, which is a bit larger than the radar distance. The reader should now take a moment to consider the case of a leading observer estimating distance to a trailing observer!
), the optical distance is a bit larger than the ruler distance, which is a bit larger than the radar distance. The reader should now take a moment to consider the case of a leading observer estimating distance to a trailing observer!There are other notions of distance, but the main point is clear: while the values of these various notions will in general disagree for a given pair of Rindler observers, they all agree that every pair of Rindler observers maintains constant distance. The fact that very nearby Rindler observers are mutually stationary follows from the fact, noted above, that the expansion tensor of the Rindler congruence vanishes identically. However, we have shown here that in various senses, this rigidity property holds at larger scales. This is truly a remarkable rigidity property, given the well-known fact that in relativistic physics, no rod can be accelerated rigidly (and no disk can be spun up rigidly) — at least, not without sustaining inhomogeneous stresses. The easiest way to see this is to observe that in Newtonian physics, if we "kick" a rigid body, all elements of matter in the body will immediately change their state of motion. This is of course incompatible with the relativistic principle that no information having any physical effect can be transmitted faster than the speed of light.
It follows that if a rod is accelerated by some external force applied anywhere along its length, the elements of matter in various different places in the rod cannot all feel the same magnitude of acceleration if the rod is not to extend without bound and ultimately break. In other words, an accelerated rod which does not break must sustain stresses which vary along its length. Furthermore, in any thought experiment with time varying forces, whether we "kick" an object or try to accelerate it gradually, we cannot avoid the problem of avoiding mechanical models which are inconsistent with relativistic kinematics (because distant parts of the body respond too quickly to an applied force).
Returning to the question of the operational significance of the ruler distance, we see that this should be the distance which our observers will obtain should they very slowly pass from hand to hand a small ruler which is repeatedly set end to end. But justifying this interpretation in detail would require some kind of material model.
Generalization to curved spacetimes
Rindler coordinates described above can be generalized to curved spacetime, and are called as Fermi normal coordinates. The generalization essential involves constructing an appropriate orthonormal tetrad and then transporting it along the given trajectory using the Fermi-Walker transport rule. For details, see the paper by Ni and Zimmermann in the references below. Such a generalization actually enables one to study inertial and gravitational effects in an Earth based laboratory, as well as the more interesting coupled inertial-gravitational effects.See also
- Bell's spaceship paradoxBell's spaceship paradoxBell's spaceship paradox is a thought experiment in special relativity involving accelerated spaceships and strings. The results of this thought experiment are for many people paradoxical. While J. S. Bell's 1976 version of the paradox is the most widely known, it was first designed by E. Dewan and M...
, for a sometimes controversial subject often studied using Rindler coordinates. - Born coordinatesBorn coordinatesIn relativistic physics, the Born coordinate chart is a coordinate chart for Minkowski spacetime, the flat spacetime of special relativity. It is often used to analyze the physical experience of observers who ride on a ring or disk rigidly rotating at relativistic speeds...
, for another important coordinate system adapted to the motion of certain accelerated observers in Minkowski spacetime. - Congruence (general relativity)Congruence (general relativity)In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
- Ehrenfest paradoxEhrenfest paradoxThe Ehrenfest paradox concerns the rotation of a "rigid" disc in the theory of relativity.In its original formulation as presented by Paul Ehrenfest 1909 in the Physikalische Zeitschrift, it discusses an ideally rigid cylinder that is made to rotate about its axis of symmetry...
, for a sometimes controversial subject often studied using Born coordinates. - Frame fields in general relativityFrame fields in general relativityIn general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
- General relativity resources
- Milne modelMilne modelThe Milne model was a special relativistic cosmological model proposed by Edward Arthur Milne in 1935. It is mathematically equivalent to a special case of the FLRW model in the limit of zero energy density , and it obeys the cosmological principle...
- Raychaudhuri equationRaychaudhuri equationIn general relativity, the Raychaudhuri equation, or Landau-Raychaudhuri equation, is a fundamental result describing the motion of nearby bits of matter....
- Unruh effectUnruh effectThe Unruh effect , was first described by Stephen Fulling in 1973, Paul Davies in 1975 and Bill Unruh in 1976. It is the prediction that an accelerating observer will observe black-body radiation where an inertial observer would observe none...

