
Anyon
Encyclopedia
In physics
, an anyon is a type of particle that occurs only in two-dimensional systems. It is a generalization of the fermion
and boson
concept.
working at the University of Oslo
, led by Jon Leinaas and Jan Myrheim, calculated in 1977 that the traditional division between fermions and bosons would not apply to theoretical particles existing in two dimension
s. Such particles would be expected to exhibit a diverse range of previously unexpected properties. They were given the name anyons by Frank Wilczek in 1982. The associated mathematics proved to be useful to Bertrand Halperin
at Harvard University
in explaining aspects of the fractional quantum Hall effect
. Frank Wilczek, Dan Arovas, and Robert Schrieffer verified this statement in 1985 with an explicit calculation that predicted that particles existing in these systems are in fact anyons.
In 2005 a group of physicists at Stony Brook University constructed a quasiparticle interferometer, detecting the patterns caused by interference of anyons which were interpreted to suggest that anyons are real, rather than just a mathematical construct. However, these experiments remain controversial and are not fully accepted by the community.
With developments in semiconductor
technology meaning that the deposition of thin two-dimensional layers is possible – for example in sheets of graphene
– the long term potential to use the properties of anyons in electronics is being explored.
. In the language of quantum physics this is formulated as the behavior of multiparticle states under the exchange of particles. This is in particular for a two-particle state (in Dirac notation):
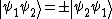
(where the first entry in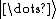 is the state of particle 1 and the second entry is the state of particle 2. So for example the left hand side is read as "Particle 1 is in state
is the state of particle 1 and the second entry is the state of particle 2. So for example the left hand side is read as "Particle 1 is in state 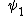 and particle 2 in state
and particle 2 in state 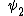 "). Here the "+" corresponds to both particles being Bosons and the "−" to both particles being Fermions (composite states of Fermions and Bosons are irrelevant since that would make them distinguishable).
"). Here the "+" corresponds to both particles being Bosons and the "−" to both particles being Fermions (composite states of Fermions and Bosons are irrelevant since that would make them distinguishable).
In two-dimensional systems, however, quasiparticle
s can be observed which obey statistics ranging continuously between Fermi–Dirac and Bose–Einstein statistics, as was first shown by Jon Magne Leinaas and Jan Myrheim of the University of Oslo in 1977. In our above example of two particles this looks as follows:
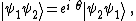
with i being the imaginary unit
and θ a real number
. Recall that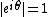 and
and 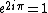 as well as
as well as  . So in the case
. So in the case 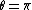 we recover the Fermi–Dirac statistics (minus sign) and in the case θ = 0 (or
we recover the Fermi–Dirac statistics (minus sign) and in the case θ = 0 (or 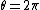 ) the Bose–Einstein statistics (plus sign). In between we have something different. Frank Wilczek coined the term "anyon" to describe such particles, since they can have any phase when particles are interchanged.
) the Bose–Einstein statistics (plus sign). In between we have something different. Frank Wilczek coined the term "anyon" to describe such particles, since they can have any phase when particles are interchanged.
We also may use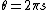 with particle spin quantum number s, with s being integer
with particle spin quantum number s, with s being integer
for Bosons, half-integer
for Fermions, so that
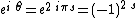 or
or 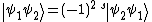 .
.
At an edge, fractional quantum Hall effect anyons are confined to move in one space dimension. Mathematical models of one dimensional anyons provide a base of the commutation relations shown above.
Just as how the Fermion and Boson wavefunctions in a three dimensional space are just 1-dimensional representations of the Permutation group
(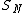 of N indistinguishable particles), the anyonic wavefunctions in a two dimensional space are just 1-dimensional representations of the Braid group (
of N indistinguishable particles), the anyonic wavefunctions in a two dimensional space are just 1-dimensional representations of the Braid group (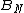 of N indistinguishable particles). Please note that anyonic statistics must not be confused with parastatistics
of N indistinguishable particles). Please note that anyonic statistics must not be confused with parastatistics
which describes statistics of particles whose wavefunctions are higher dimensional representations of the permutation group.
states that any multiparticle state has to obey either Bose–Einstein or Fermi–Dirac statistics. For any d>2, the group
SO(d,1)
(which generalize the Lorentz group
), and also Poincaré(d,1)
, have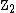 as their first homotopy group.
as their first homotopy group. 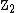 is the cyclic group
is the cyclic group
consisting of two elements, therefore only two possibilities remain. (The details are more involved than that, but this is the crucial point.)
The situation changes in two dimensions. Here the first homotopy group of SO(2,1), and also Poincaré(2,1), is Z (infinite cyclic). This means that Spin(2,1) is not the universal cover
: it is not simply connected. In detail, there are projective representation
s of the special orthogonal group
SO(2,1) which do not arise from linear representations of SO(2,1), or of its double cover, the spin group Spin(2,1). These representations are called anyons.
This concept also applies to nonrelativistic systems. The relevant part here is that the spatial rotation group is SO(2) has an infinite first homotopy group.
This fact is also related to the braid group
s well known in knot theory
. The relation can be understood when one considers the fact that in two dimensions the group of permutations of two particles is no longer the symmetric group
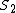 (with two elements) but rather the braid group
(with two elements) but rather the braid group  (with an infinite number of elements). The essential point is that one braid can wind around the other one, an operation that can be performed infinitely often, and clockwise as well as counterclockwise.
(with an infinite number of elements). The essential point is that one braid can wind around the other one, an operation that can be performed infinitely often, and clockwise as well as counterclockwise.
A very different approach to the stability-decoherence problem in quantum computing
is to create a topological quantum computer
with anyons, quasi-particles used as threads and relying on braid theory
to form stable logic gates.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, an anyon is a type of particle that occurs only in two-dimensional systems. It is a generalization of the fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
and boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
concept.
From theory to reality
A group of theoretical physicistsTheoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
working at the University of Oslo
University of Oslo
The University of Oslo , formerly The Royal Frederick University , is the oldest and largest university in Norway, situated in the Norwegian capital of Oslo. The university was founded in 1811 and was modelled after the recently established University of Berlin...
, led by Jon Leinaas and Jan Myrheim, calculated in 1977 that the traditional division between fermions and bosons would not apply to theoretical particles existing in two dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s. Such particles would be expected to exhibit a diverse range of previously unexpected properties. They were given the name anyons by Frank Wilczek in 1982. The associated mathematics proved to be useful to Bertrand Halperin
Bertrand Halperin
Bertrand I. Halperin is the Hollis Professor of Mathematics and Natural Philosophy at the physics department of Harvard University.He grew up in Crown Heights, Brooklyn. He attended Harvard University , and did his graduate work at Berkeley with John J. Hopfield .In the 1970s, he, together with...
at Harvard University
Harvard University
Harvard University is a private Ivy League university located in Cambridge, Massachusetts, United States, established in 1636 by the Massachusetts legislature. Harvard is the oldest institution of higher learning in the United States and the first corporation chartered in the country...
in explaining aspects of the fractional quantum Hall effect
Fractional quantum Hall effect
The fractional quantum Hall effect is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantised plateaus at fractional values of e^2/h. It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations...
. Frank Wilczek, Dan Arovas, and Robert Schrieffer verified this statement in 1985 with an explicit calculation that predicted that particles existing in these systems are in fact anyons.
In 2005 a group of physicists at Stony Brook University constructed a quasiparticle interferometer, detecting the patterns caused by interference of anyons which were interpreted to suggest that anyons are real, rather than just a mathematical construct. However, these experiments remain controversial and are not fully accepted by the community.
With developments in semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
technology meaning that the deposition of thin two-dimensional layers is possible – for example in sheets of graphene
Graphene
Graphene is an allotrope of carbon, whose structure is one-atom-thick planar sheets of sp2-bonded carbon atoms that are densely packed in a honeycomb crystal lattice. The term graphene was coined as a combination of graphite and the suffix -ene by Hanns-Peter Boehm, who described single-layer...
– the long term potential to use the properties of anyons in electronics is being explored.
In physics
In space of three or more dimensions, indistinguishable particles are restricted to being Fermions or Bosons, according to their statistical behaviour. Fermions respect the so-called Fermi–Dirac statistics while Bosons respect the Bose–Einstein statisticsBose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
. In the language of quantum physics this is formulated as the behavior of multiparticle states under the exchange of particles. This is in particular for a two-particle state (in Dirac notation):
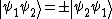
(where the first entry in
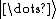 is the state of particle 1 and the second entry is the state of particle 2. So for example the left hand side is read as "Particle 1 is in state
is the state of particle 1 and the second entry is the state of particle 2. So for example the left hand side is read as "Particle 1 is in state 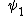 and particle 2 in state
and particle 2 in state 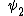 "). Here the "+" corresponds to both particles being Bosons and the "−" to both particles being Fermions (composite states of Fermions and Bosons are irrelevant since that would make them distinguishable).
"). Here the "+" corresponds to both particles being Bosons and the "−" to both particles being Fermions (composite states of Fermions and Bosons are irrelevant since that would make them distinguishable).In two-dimensional systems, however, quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
s can be observed which obey statistics ranging continuously between Fermi–Dirac and Bose–Einstein statistics, as was first shown by Jon Magne Leinaas and Jan Myrheim of the University of Oslo in 1977. In our above example of two particles this looks as follows:
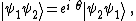
with i being the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
and θ a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Recall that
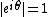 and
and 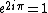 as well as
as well as  . So in the case
. So in the case 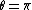 we recover the Fermi–Dirac statistics (minus sign) and in the case θ = 0 (or
we recover the Fermi–Dirac statistics (minus sign) and in the case θ = 0 (or 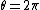 ) the Bose–Einstein statistics (plus sign). In between we have something different. Frank Wilczek coined the term "anyon" to describe such particles, since they can have any phase when particles are interchanged.
) the Bose–Einstein statistics (plus sign). In between we have something different. Frank Wilczek coined the term "anyon" to describe such particles, since they can have any phase when particles are interchanged.We also may use
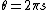 with particle spin quantum number s, with s being integer
with particle spin quantum number s, with s being integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
for Bosons, half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
for Fermions, so that
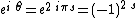 or
or 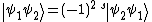 .
.At an edge, fractional quantum Hall effect anyons are confined to move in one space dimension. Mathematical models of one dimensional anyons provide a base of the commutation relations shown above.
Just as how the Fermion and Boson wavefunctions in a three dimensional space are just 1-dimensional representations of the Permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
(
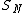 of N indistinguishable particles), the anyonic wavefunctions in a two dimensional space are just 1-dimensional representations of the Braid group (
of N indistinguishable particles), the anyonic wavefunctions in a two dimensional space are just 1-dimensional representations of the Braid group (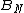 of N indistinguishable particles). Please note that anyonic statistics must not be confused with parastatistics
of N indistinguishable particles). Please note that anyonic statistics must not be confused with parastatisticsParastatistics
In quantum mechanics and statistical mechanics, parastatistics is one of several alternatives to the better known particle statistics models...
which describes statistics of particles whose wavefunctions are higher dimensional representations of the permutation group.
Topological basis
In more than two dimensions, the spin-statistics connectionSpin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
states that any multiparticle state has to obey either Bose–Einstein or Fermi–Dirac statistics. For any d>2, the group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
SO(d,1)
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
(which generalize the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
), and also Poincaré(d,1)
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
, have
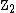 as their first homotopy group.
as their first homotopy group. 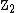 is the cyclic group
is the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
consisting of two elements, therefore only two possibilities remain. (The details are more involved than that, but this is the crucial point.)
The situation changes in two dimensions. Here the first homotopy group of SO(2,1), and also Poincaré(2,1), is Z (infinite cyclic). This means that Spin(2,1) is not the universal cover
Universal covering group
In mathematics, a covering group of a topological group H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism. The map p is called the covering homomorphism...
: it is not simply connected. In detail, there are projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s of the special orthogonal group
Generalized orthogonal group
In mathematics, the indefinite orthogonal group, O is the Lie group of all linear transformations of a n = p + q dimensional real vector space which leave invariant a nondegenerate, symmetric bilinear form of signature...
SO(2,1) which do not arise from linear representations of SO(2,1), or of its double cover, the spin group Spin(2,1). These representations are called anyons.
This concept also applies to nonrelativistic systems. The relevant part here is that the spatial rotation group is SO(2) has an infinite first homotopy group.
This fact is also related to the braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s well known in knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
. The relation can be understood when one considers the fact that in two dimensions the group of permutations of two particles is no longer the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
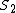 (with two elements) but rather the braid group
(with two elements) but rather the braid group  (with an infinite number of elements). The essential point is that one braid can wind around the other one, an operation that can be performed infinitely often, and clockwise as well as counterclockwise.
(with an infinite number of elements). The essential point is that one braid can wind around the other one, an operation that can be performed infinitely often, and clockwise as well as counterclockwise.A very different approach to the stability-decoherence problem in quantum computing
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
is to create a topological quantum computer
Topological quantum computer
A topological quantum computer is a theoretical quantum computer that employs two-dimensional quasiparticles called anyons, whose world lines cross over one another to form braids in a three-dimensional spacetime . These braids form the logic gates that make up the computer...
with anyons, quasi-particles used as threads and relying on braid theory
Braid theory
In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a...
to form stable logic gates.

