Braid group

	Email		Print
	Bookmark		Link

Braid group

In mathematics

Mathematics

Mathematics is the study of quantity, structure, space, change, and related topics of pattern and form. Mathematicians seek out patterns whether found in numbers, space, natural science, computers, imaginary abstractions, or elsewhere....
, the braid group on n strands, denoted by B_n, is a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an Binary operation that combines any two of its element to form a third element....
which has an intuitive geometrical representation, and in a sense generalizes the symmetric group

Symmetric group

In mathematics, the symmetric group on a Set X, denoted by SX, or Sym, is the group whose underlying set is the set of all bijective function s from X to X, in which the group operation is that of Function composition, i.e., two such functions f and g can be composed to yield a new bijective function ,...
S_n. Here, n is a natural number

Natural number

In mathematics, a natural number can mean either an element of the Set = *n = = ? = ? ...
; if n > 1, then B_n is an infinite group. Braid groups find applications in knot theory

Knot theory

In mathematics, knot theory is the area of topology that studies knot s. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs drastically in that the ends are joined together to prevent it from becoming undone....
, since any knot may be represented as the closure of certain braids.

Intuitive description
This introduction takes n to be 4; the generalization to other values of n will be straightforward.

Discussion

Ask a question about 'Braid group'

Start a new discussion about 'Braid group'

Answer questions from other users

Full Discussion Forum

Encyclopedia

In mathematics

Mathematics

Group (mathematics)

Symmetric group

Natural number

In mathematics, a natural number can mean either an element of the Set = *n = = ? = ? ...
; if n > 1, then B_n is an infinite group. Braid groups find applications in knot theory

Knot theory

Intuitive description

This introduction takes n to be 4; the generalization to other values of n will be straightforward. Consider two sets of four items lying on a table, with the items in each set being arranged in a vertical line, and such that one set sits next to the other. (In the illustrations below, these are the black dots.) Using four strands, each item of the first set is connected with an item of the second set so that a one-to-one correspondence results. Such a connection is called a braid. Often some strands will have to pass over or under others, and this is crucial: the following two connections are different braids:

is different from

On the other hand, two such connections which can be made to look the same by "pulling the strands" are considered the same braid:

is the same as

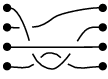
All strands are required to move from left to right; knots like the following are not considered braids:

is not a braid

Any two braids can be composed by drawing the first next to the second, identifying the four items in the middle, and connecting corresponding strands:

composed with

yields

Another example:

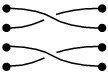
composed with

yields

The composition of the braids s and t is written as st.

The set of all braids on four strands is denoted by B₄. The above composition of braids is indeed a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an Binary operation that combines any two of its element to form a third element....
operation. The neutral element is the braid consisting of four parallel horizontal strands, and the inverse

Inverse element

In mathematics, the idea of inverse element generalises the concepts of additive inverse, in relation to addition, and Multiplicative inverse, in relation to multiplication....
of a braid consists of that braid which "undoes" whatever the first braid did. (The first two example braids above are inverses of each other.)

Generators and relations

Consider the following three braids:

s₁


s₂	s₃ >

Every braid in B₄ can be written as a composition of a number of these braids and their inverses. In other words, these three braids generate

Generating set of a group

In abstract algebra, a generating set of a group is a subset S such that every element of G can be expressed as the product of finitely many elements of S and their inverses....
the group B₄. To see this, an arbitrary braid is scanned from left to right; whenever a crossing of strands i and i + 1 (counting from the top at the point of the crossing) is encountered, s_i or s_i⁻¹ is written down, depending on whether strand i moves under or over strand i + 1. Upon reaching the right hand end, the braid has been written as a product of the s's and their inverses.

It is clear that

s₁s₃ = s₃s₁,

while the following two relations are not quite as obvious:

s₁s₂s₁ = s₂s₁s₂

s₂s₃s₂ = s₃s₂s₃

(these can be appreciated best by drawing the braid on a piece of paper). It can be shown that all other relations among the braids s₁, s₂ and s₃ already follow from these relations and the group axioms.

Generalising this example to n strands, the group B_n can be abstractly defined via the following presentation

Presentation of a group

generators s₁,...,s_n−1
relations (known as the braid or Artin
Artin

Artin may refer to:*The name of a king of Panda, still in use among modern Iranians today.*Emil Artin, was an Austrian mathematician.*Michael Artin, is an American mathematician, son of Emil Artin....
relations):

s_i s_j = s_j s_i whenever |i − j| = 2 ;
s_is_i+1 s_i = s_i+1 s_i s_i+1 for i = 1,..., n − 2 (sometimes called the Yang-Baxter equation
Yang-Baxter equation

The Yang?Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C....
)

Some properties

The groups B₀ and B₁ are trivial; B₂ is an infinite cyclic group

Cyclic group

In group theory, a cyclic group or monogenous group is a group that can be generating set of a group by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g ....
. B₃ is a non-abelian

Abelian group

An abelian group, also called a commutative group, is a group satisfying the requirement that the product of elements does not depend on their order ....
infinite group; in fact, B₃ is isomorphic to the knot group

Knot group

In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,...
of the trefoil

Trefoil knot

In knot theory, the trefoil knot is the simplest nontrivial knot . It can be obtained by joining the loose ends of an overhand knot. It can be described as a -torus knot, and is the closure of the 2-stranded braid group s1?....
.

Provided , contains a free group on two generators, and so it is not abelian.

B_n is a subgroup

Subgroup

In group theory, given a group G under a binary operation *, we say that some subset H of G is a subgroup of G if H also forms a group under the operation *....
of B_n + 1: it can be viewed as consisting of all those braids on n + 1 strands in which the bottom strand is horizontal and does not cross nor is crossed by any other strand. The formal union of all the braid groups is sometimes called the infinite braid group.

There is a useful notion of "length" for the elements of the braid group, given by the group homomorphism

Group homomorphism

In mathematics, given two group and , a group homomorphism from to is a function h : G ? H such that for all u and v in G it holds that...
B_n ? Z that maps every s_i to 1. So for instance, the length of the braid s₂s₃s₁⁻¹s₂s₃ is 1 + 1 − 1 + 1 + 1 = 3. This notion gives rise, for example, to the subgroup

Subgroup

In group theory, given a group G under a binary operation *, we say that some subset H of G is a subgroup of G if H also forms a group under the operation *....
of B_n consisting of all even

Even and odd numbers

In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2....
-length braids.

B_n is torsion-free.

Via the mapping-class group interpretation of braids, all braids have a classification as either periodic, reducible or pseudo-Anosov

Nielsen-Thurston classification

In mathematics, Thurston's classification theorem characterizes homeomorphisms of a compact surface. William Thurston's theorem completes the work initiated by Jakob Nielsen in the 1930s....
.

B_n is known to be a subgroup

Subgroup

In group theory, given a group G under a binary operation *, we say that some subset H of G is a subgroup of G if H also forms a group under the operation *....
of the unitary group

Unitary group

In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrix, with the group operation that of matrix multiplication....
. The embedding is given by the Lawrence-Krammer representation where the variables are specialized to suitable algebraically-independent unit complex numbers.

Relation to the symmetric group, group actions

Every braid on n strands basically consists of a one-to-one correspondence between two sets of n items, and some topological information about how the strands establish this correspondence. Without this topological information every braid yields a one-to-one correspondence of n items; these are precisely the elements of the symmetric group

Symmetric group

Group homomorphism

In mathematics, given two group and , a group homomorphism from to is a function h : G ? H such that for all u and v in G it holds that...
B_n ? S_n.

The kernel

Kernel (algebra)

In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective....
of this group homomorphism is called the pure braid group on n strands ; it consists of those braids which connect the i-th item of the left set to the i-th item of the right set, for all i. There are split group extensions ie: pure braid groups are iterated semi-direct products

Semidirect product

In mathematics, especially in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup....
of free groups.

The symmetric group S_n has a very similar presentation to the one given above for the braid group: taking the braid relations and adding the relations

s_i² = 1 for i = 1, ..., n − 1

yields a presentation for S_n (the s_i can then be thought of as transposition

Transposition (mathematics)

In informal language, a transposition is a function that swaps two elements of a set. More formally, given a finite set Set , a transposition is a permutation such that there exist indices such that , and for all other indices This is often denoted as ...
s of two neighboring elements).

In situations where n items are being permuted "up to a twist", there is often an underlying group action

Group action

In algebra and geometry, a group action is a way of describing symmetry of objects using group . The essential elements of the object are described by a Set and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformation of the set....
of the braid group B_n. As a prototypical example, consider an arbitrary group G and the set X of all n-tuples of elements of G whose product is 1, the identity element

Identity element

In mathematics, an identity element is a special type of element of a Set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them....
of G. Then B_n operates on X in the following natural fashion: given a tuple x = (x₁, ..., x_n) in X define s_i.x = (x₁, ..., x_i−1, x_i+1, x_i+1⁻¹x_ix_i+1, x_i+2, ..., x_n), so x_i and x_i+1 exchange places, but x_i is in addition "twisted" by the inner automorphism

Inner automorphism

In abstract algebra, an inner automorphism of a group G is a function defined bywhere a is a given fixed element of G.The operation axa-1 is called conjugation ....
corresponding to x_i+1; this twist ensures that the product of the components of s_i.x is the same as that of the components of x, namely 1. This operation satisfies the braid relations and thus defines a group action of B_n on X.

Relation between B₃ and the modular group

There is a surjective homomorphism from B₃ onto the modular group

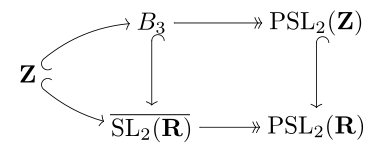Modular group

In mathematics, the modular group G is a fundamental object of study in number theory, geometry, abstract algebra, and many other areas of advanced mathematics....
with kernel

Kernel (algebra)

Center (group theory)

In abstract algebra, the center of a group G is the set Z of all elements in G which Commutative with all the elements of G. That is,...
of B₃; a construction is given below.

Define and . From the braid relations it follows that . Denoting this latter product as , one may verify from the braid relations that

implying that is in the center of B₃. The subgroup

Subgroup

In group theory, given a group G under a binary operation *, we say that some subset H of G is a subgroup of G if H also forms a group under the operation *....
of B₃ generated by is therefore a normal subgroup

Normal subgroup

In mathematics, more specifically in abstract algebra, a normal subgroup is a special kind of subgroup. Normal subgroups are important because they can be used to construct quotient groups from a given group ....
. Since it is normal, one may take the quotient group

Quotient group

In mathematics, given a group G and a normal subgroup N of G, the quotient group, or factor group, of G over N is intuitively a group that "collapses" the normal subgroup N to the identity element....
; this quotient group is isomorphic to the modular group:

This isomorphism can be given an explicit form. The coset

Coset

In mathematics, if G is a group , H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G....
s of and of map to

where and are the standard left and right moves on the Stern-Brocot tree

Stern-Brocot tree

In number theory, the Stern-Brocot tree is a method of listing all non-negative rational numbers in a tree structure. It was discovered independently by Moritz Stern and Achille Brocot ....
; it is well known that these moves generate the modular group. Alternately, one common presentation

Presentation of a group

In mathematics, one method of defining a group is by a presentation. One specifies a set S of generating set of a group so that every element of the group can be written as a product of some of these generators, and a set R of relations among those generators....
for the modular group is

where

and

with

the latter being the identity element of .

The center of B₃ is equal to , a consequence of the facts that c is in the center, the modular group has trivial center, and the above surjective homomorphism has kernel

Kernel (algebra)

In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective....
.

Relationship to the mapping class group and the monodromy

The braid group B_n can be shown to be the mapping class group

Mapping class group

In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space....
of a punctured disk with n punctures. This is most easily visualized by imagining each puncture as being connected by a string to the boundary of the disk; each mapping homeomorphism that permutes two of the punctures can then be seen to be a homotopy of the strings, that is, a braiding of these strings.

The braid group may be mapped onto the monodromy

Monodromy

Analytic function

In mathematics, an analytic function is a function that is locally given by a convergent power series. Analytic functions can be thought of as a bridge between polynomials and general functions....
. This may be visualized by considering a disk with n-1 punctures, each puncture corresponding to a pole of the analytic function. The monodromy can then be visualized by taking each of the punctures to be a straight line perpendicular to the disk, and the monodromy path as a string, anchored at a point, that winds around each of the punctures, returning to its original starting point.

Connection to knot theory and computational aspects

If a braid is given and one connects the first left-hand item to the first right-hand item using a new string, the second left-hand item to the second right-hand item etc. (without creating any braids in the new strings), one obtains a link

Link (knot theory)

In mathematics, a link is a collection of knot s which do not intersect, but which may be linked together. A knot can be described as a link with one component....
, and sometimes a knot

Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations ....
. Alexander's theorem in braid theory

Braid theory

In topology, braid theory is an abstract geometry theory studying the everyday braid concept, and some generalisations. The idea is that braids can be organised into group s, in which the group operation is 'do the first braid on a set of strings, and then follow it with a second on the twisted strings'....
states that the converse is true as well: every knot

Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations ....
and every link

Link (knot theory)

In mathematics, a link is a collection of knot s which do not intersect, but which may be linked together. A knot can be described as a link with one component....
arises in this fashion from at least one braid; such a braid can be obtained by cutting the link. Since braids can be concretely given as words in the generators s_i, this is often the preferred method of entering knots into computer programs.

The word problem

Word problem for groups

In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a presentation of a group group G is the algorithmic problem of deciding whether two words represent the same element....
for the braid relations is efficiently solvable and there exists a normal form

Normal form

Normal form is a term that may refer to:* Database normalization#Normal forms* Normal form game* Normal form In formal language theory:* Beta normal form...
for elements of B_n in terms of the generators s₁,...,s_n−1. (In essence, computing the normal form of a braid is the algebraic analogue of "pulling the strands" as illustrated in our second set of images above.) The free GAP computer algebra system

GAP computer algebra system

GAP is a computer algebra system for computational discrete algebra with particular emphasis on computational group theory. GAP was developed at Lehrstuhl D f?r Mathematik , RWTH Aachen, Germany from 1986 to 1997....
can carry out computations in B_n if the elements are given in terms of these generators. There is also a package called CHEVIE for GAP3 with special support for braid groups. The word problem is also efficiently solved via the Lawrence-Krammer representation.

Since there are nevertheless several hard computational problems about braid groups, applications in cryptography

Cryptography

Cryptography is the practice and study of hiding information. In modern times cryptography is considered a branch of both mathematics and computer science and is affiliated closely with information theory, computer security and engineering....
have been suggested.

Representations

Frequently referenced representations

Group representation

In the mathematics field of representation theory, group representations describe abstract group in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrix so that the group operation can be represented by matrix multiplication....
of the braid groups include the Burau representation

Burau representation

In mathematics the Burau representation is a group representation of the braid groups. The Burau representation has two common and near-equivalent formulations, the reduced and unreduced Burau representations....
, the Lawrence-Krammer representation and the Lawrence representations.

Infinitely generated braid groups

There are many ways to generalize this notion to an infinite number of strands. The simplest way is take the direct limit

Direct limit

In mathematics, a direct limit is a limit of a "directed family of objects". We will first give the definition for algebraic structures like group and module , and then the general definition which can be used in any category ....
of braid groups, where the attaching maps send the generators of to the first generators of (i.e., by attaching a trivial strand). Fabel has shown that there are two topologies

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connected space, and Continuous function ....
that can be imposed on the resulting group each of whose completion yields a different group. One is a very tame group and is isomorphic to the mapping class group

Mapping class group

Unit disk

In mathematics, the open unit disk around P , is the set of points whose distance from P is less than 1:The closed unit disk around P is the set of points whose distance from P is less than or equal to one:...
.

The second group can be thought of the same as with finite braid groups. Place a strand at each of the points and the set of all braids — where a braid is defined to be a collection of paths from the points to the points so that the function yields a permutation on endpoints — is isomorphic to this wilder group. An interesting fact is that the pure braid group in this group is isomorphic to both the inverse limit

Inverse limit

In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects....
of finite pure braid groups and to the fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group or Poincar? group is a group associated to any given pointed space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other....
of the Hilbert cube

Hilbert cube

In mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology....
minus the set .

Formal treatment

To put the above informal discussion of braid groups on firm ground, one needs to use the homotopy

Homotopy

In topology, two continuous function Function from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions....
concept of algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant that classification theorem topological spaces up to homeomorphism....
, defining braid groups as fundamental group

Fundamental group

Configuration space

Configuration space in physics In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints....
. This is outlined in the article on braid theory

Braid theory

In topology, braid theory is an abstract geometry theory studying the everyday braid concept, and some generalisations. The idea is that braids can be organised into group s, in which the group operation is 'do the first braid on a set of strings, and then follow it with a second on the twisted strings'....
.

Alternatively, one can eschew topology altogether and define the braid group purely algebraically via the braid relations, keeping the pictures in mind only to guide the intuition.

History

Braid groups were introduced explicitly by Emil Artin

Emil Artin

Emil Artin was an Austrian mathematician. His father, also Emil Artin, was an Armenian art-dealer, and his mother was the opera singer Emma Laura-Artin....
in 1925, although (as Wilhelm Magnus

Wilhelm Magnus

Wilhelm Magnus was a mathematician. He made important contributions in combinatorial group theory, Lie algebras, mathematical physics, elliptic functions, and the study of tessellations....
pointed out in 1974) they were already implicit in Adolf Hurwitz

Adolf Hurwitz

Adolf Hurwitz , was a Germany mathematician, and was described by Jean-Pierre Serre as "one of the most important figures in mathematics in the second half of the nineteenth century"....
's work on monodromy

Monodromy

In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic geometry and differential geometry behave as they 'run round' a Mathematical singularity....
(1891). In fact, as Magnus says, Hurwitz gave the interpretation of a braid group as the fundamental group of a configuration space (cf. braid theory

Braid theory

In topology, braid theory is an abstract geometry theory studying the everyday braid concept, and some generalisations. The idea is that braids can be organised into group s, in which the group operation is 'do the first braid on a set of strings, and then follow it with a second on the twisted strings'....
), an interpretation that was lost from view until it was rediscovered by Ralph Fox

Ralph Fox

Ralph Hartzler Fox was an United States of America mathematician. As a professor at Princeton University, he taught and advised many of the contributors to the Golden Age of differential topology, and he played an important role in the modernization and main-streaming of knot theory....
and Lee Neuwirth in 1962.

External links

at Contains extensive library for computations with Braid Groups
P. Fabel, , Journal of Knot Theory and its Ramifications, Vol. 14, No. 8 (2005) 979-991
P. Fabel, , Journal of Knot Theory and its Ramifications, Vol. 15, No. 1 (2006) 21-29
, Encyclopaedia of Mathematics, Springer 2002
Stephen Bigelow's Java applet.

es:grupo de trenzas fa:???? ?????

Braid group

Intuitive description

Generators and relations

Some properties

Relation to the symmetric group, group actions

Relation between B3 and the modular group

Relationship to the mapping class group and the monodromy

Connection to knot theory and computational aspects

Representations

Infinitely generated braid groups

Formal treatment

History

Further reading

External links

Relation between B₃ and the modular group