
Generalized orthogonal group
Encyclopedia
In mathematics
, the indefinite orthogonal group, O(p,q) is the Lie group
of all linear transformation
s of a n = p + q dimensional real vector space
which leave invariant a nondegenerate, symmetric bilinear form
of signature (p, q). The dimension of the group is
The indefinite special orthogonal group, SO(p,q) is the subgroup
of O(p,q) consisting of all elements with determinant
1. Unlike in the definite case, SO(p,q) is not connected – it has 2 components – and there are two additional finite index subgroups, namely the connected SO+(p,q) and O+(p,q), which has 2 components – see the topology section for definition and discussion.
The signature of the metric
(p positive and q negative eigenvalues) determines the group up to isomorphism
; interchanging p with q amounts to replacing the metric by its negative, and so gives the same group. If either p or q equals zero, then the group is isomorphic to the ordinary orthogonal group
O(n). We assume in what follows that both p and q are positive.
The group O(p,q) is defined for vector spaces over the real
s. For complex
spaces, all groups O(p,q; C) are isomorphic to the usual orthogonal group
O(p + q; C), since the transform changes the signature of a form.
changes the signature of a form.
In even dimension, the middle group O(n,n) is known as the split orthogonal group, and is of particular interest. In odd dimension, the corresponding almost-middle group O(n,n+1) is known as the quasi-split orthogonal group, and plays a similar role.
s, which is the group SO+(1,1) of (the identity component of) linear transforms preserving the unit hyperbola
. Concretely, these are the matrices and can be interpreted as hyperbolic rotations, just as the group SO(2) can be interpreted as circular rotations. In physics, the Lorentz group
and can be interpreted as hyperbolic rotations, just as the group SO(2) can be interpreted as circular rotations. In physics, the Lorentz group
O(1,3) is of central importance, being the setting for electromagnetism
and special relativity
.
, just as for the classical orthogonal group O(n). The standard inner product on Rp,q is given in coordinates by the diagonal matrix
: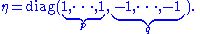
As a quadratic form,
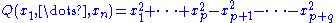
The group O(p,q) is then the group of a n×n matrices M (where n = p+q) such that ; as a bilinear form,
; as a bilinear form,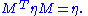
Here MT denotes the transpose
of the matrix M. One can easily verify that the set of all such matrices forms a group. The inverse of M is given by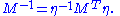
One obtains an isomorphic group (indeed, a conjugate subgroup of GL(V)) by replacing η with any symmetric matrix with p positive eigenvalues and q negative ones (such a matrix is necessarily nonsingular); equivalently, any quadratic form with signature (p,q). Diagonalizing this matrix gives a conjugation of this group with the standard group O(p,q).
, having four and two components respectively.
is the Klein four-group
, with each factor being whether an element preserves or reverses the respective orientations on the p and q dimensional subspaces on which the form is definite.
The special orthogonal group has components } which either preserves both orientations or reverses both orientations.
The identity component
of O(p,q) is often denoted SO+(p,q) and can be identified with the set of elements in SO(p,q) which preserves both orientations.
The group O(p,q) is also not compact
, but contains the compact subgroups O(p) and O(q) acting on the subspaces on which the form is definite. In fact, is a maximal compact subgroup
of O(p,q), while is a maximal compact subgroup of SO(p,q).
Likewise, is a maximal compact subgroup of SO+(p, q).
Thus up to homotopy, the spaces are products of (special) orthogonal groups, from which algebro-topological invariants can be computed.
In particular, the fundamental group
of SO+(p,q) is the product of the fundamental groups of the components, , and is given by:
so2n (the Lie group of the split real form of the Lie algebra); more precisely, the identity component is the split Lie group, as non-identity components cannot be reconstructed from the Lie algebra. In this sense it is opposite to the definite orthogonal group O(n) := O(n,0) = O(0,n), which is the compact real form of the complex Lie algebra.
The case (1,1) corresponds to the split-complex number
s.
In terms of being a group of Lie type
– i.e., construction of an algebraic group from a Lie algebra – split orthogonal groups are Chevalley groups, while the non-split orthogonal groups require a slightly more complicated construction, and are Steinberg group
s.
Split orthogonal groups are used to construct the generalized flag variety over non-algebraically closed fields.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the indefinite orthogonal group, O(p,q) is the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of all linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of a n = p + q dimensional real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
which leave invariant a nondegenerate, symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
of signature (p, q). The dimension of the group is
- n(n − 1)/2.
The indefinite special orthogonal group, SO(p,q) is the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of O(p,q) consisting of all elements with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1. Unlike in the definite case, SO(p,q) is not connected – it has 2 components – and there are two additional finite index subgroups, namely the connected SO+(p,q) and O+(p,q), which has 2 components – see the topology section for definition and discussion.
The signature of the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
(p positive and q negative eigenvalues) determines the group up to isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
; interchanging p with q amounts to replacing the metric by its negative, and so gives the same group. If either p or q equals zero, then the group is isomorphic to the ordinary orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n). We assume in what follows that both p and q are positive.
The group O(p,q) is defined for vector spaces over the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. For complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
spaces, all groups O(p,q; C) are isomorphic to the usual orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(p + q; C), since the transform
 changes the signature of a form.
changes the signature of a form.In even dimension, the middle group O(n,n) is known as the split orthogonal group, and is of particular interest. In odd dimension, the corresponding almost-middle group O(n,n+1) is known as the quasi-split orthogonal group, and plays a similar role.
Examples
The basic example is the squeeze mappingSqueeze mapping
In linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
s, which is the group SO+(1,1) of (the identity component of) linear transforms preserving the unit hyperbola
Unit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
. Concretely, these are the matrices
 and can be interpreted as hyperbolic rotations, just as the group SO(2) can be interpreted as circular rotations. In physics, the Lorentz group
and can be interpreted as hyperbolic rotations, just as the group SO(2) can be interpreted as circular rotations. In physics, the Lorentz groupLorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
O(1,3) is of central importance, being the setting for electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
and special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
Matrix definition
One can define O(p,q) as a group of matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, just as for the classical orthogonal group O(n). The standard inner product on Rp,q is given in coordinates by the diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
:
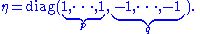
As a quadratic form,
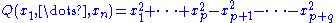
The group O(p,q) is then the group of a n×n matrices M (where n = p+q) such that
 ; as a bilinear form,
; as a bilinear form,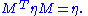
Here MT denotes the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the matrix M. One can easily verify that the set of all such matrices forms a group. The inverse of M is given by
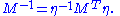
One obtains an isomorphic group (indeed, a conjugate subgroup of GL(V)) by replacing η with any symmetric matrix with p positive eigenvalues and q negative ones (such a matrix is necessarily nonsingular); equivalently, any quadratic form with signature (p,q). Diagonalizing this matrix gives a conjugation of this group with the standard group O(p,q).
Topology
Assuming both p and q are nonzero, neither of the groups O(p,q) or SO(p,q) are connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, having four and two components respectively.
is the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
, with each factor being whether an element preserves or reverses the respective orientations on the p and q dimensional subspaces on which the form is definite.
The special orthogonal group has components } which either preserves both orientations or reverses both orientations.
The identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of O(p,q) is often denoted SO+(p,q) and can be identified with the set of elements in SO(p,q) which preserves both orientations.
The group O(p,q) is also not compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, but contains the compact subgroups O(p) and O(q) acting on the subspaces on which the form is definite. In fact, is a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of O(p,q), while is a maximal compact subgroup of SO(p,q).
Likewise, is a maximal compact subgroup of SO+(p, q).
Thus up to homotopy, the spaces are products of (special) orthogonal groups, from which algebro-topological invariants can be computed.
In particular, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of SO+(p,q) is the product of the fundamental groups of the components, , and is given by:
| π1(SO+(p,q)) | p = 1 | p = 2 | p ≥ 3 |
|---|---|---|---|
| q = 1 | {1} | Z | Z2 |
| q = 2 | Z | Z × Z |
Z × Z2 |
| q ≥ 3 | Z2 | Z2 × Z |
Z2 × Z2 |
Split orthogonal group
In even dimension, the middle group O(n,n) is known as the split orthogonal group, and is of particular interest. It is the split Lie group corresponding to the complex Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
so2n (the Lie group of the split real form of the Lie algebra); more precisely, the identity component is the split Lie group, as non-identity components cannot be reconstructed from the Lie algebra. In this sense it is opposite to the definite orthogonal group O(n) := O(n,0) = O(0,n), which is the compact real form of the complex Lie algebra.
The case (1,1) corresponds to the split-complex number
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s.
In terms of being a group of Lie type
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
– i.e., construction of an algebraic group from a Lie algebra – split orthogonal groups are Chevalley groups, while the non-split orthogonal groups require a slightly more complicated construction, and are Steinberg group
Steinberg group
In mathematics, Steinberg group means either of two distinct, though related, constructions of the mathematician Robert Steinberg:*Steinberg group St in algebraic K-theory.*Steinberg group is a 'twisted' group of Lie type....
s.
Split orthogonal groups are used to construct the generalized flag variety over non-algebraically closed fields.

