
Bose–Einstein statistics
Encyclopedia
In statistical mechanics
, Bose
–Einstein
statistics
(or more colloquially B–E statistics) determines the statistical distribution of identical indistinguishable
boson
s over the energy states in thermal equilibrium
.
are important and the particles are "indistinguishable
". Quantum effects appear if the concentration of particles satisfies N/V ≥ nq. Here nq is the quantum concentration
, for which the interparticle distance is equal to the thermal de Broglie wavelength, so that the wavefunction
s of the particles are touching but not overlapping. Fermi–Dirac statistics apply to fermions (particles that obey the Pauli exclusion principle
), and Bose–Einstein statistics apply to bosons. As the quantum concentration depends on temperature; most systems at high temperatures obey the classical (Maxwell–Boltzmann) limit unless they have a very high density, as for a white dwarf
. Both Fermi–Dirac and Bose–Einstein become Maxwell–Boltzmann statistics
at high temperature or at low concentration.
Bosons, unlike fermions, are not subject to the Pauli exclusion principle
: an unlimited number of particles may occupy the same state at the same time. This explains why, at low temperatures, bosons can behave very differently from fermions; all the particles will tend to congregate together at the same lowest-energy state, forming what is known as a Bose–Einstein condensate
.
B–E statistics was introduced for photon
s in 1924 by Bose
and generalized to atoms by Einstein
in 1924-25.
The expected number of particles in an energy state i for B–E statistics is
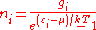
with εi > μ and where ni is the number of particles in state i, gi is the degeneracy
of state i, εi is the energy
of the ith state, μ is the chemical potential
, k is the Boltzmann constant, and T is absolute temperature
.
This reduces to the Rayleigh-Jeans distribution for , namely
, namely 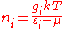 .
.
, a Bengali
professor of University of Calcutta
in British India was intrigued by Einstein
's theory of light waves being made of particles called photons. Bose was interested in mathematically deriving Planck's radiation formula, which Planck obtained largely by guessing. In 1900 Max Planck
had derived his formula by manipulating the mathematics to fit the empirical evidence. Using the particle picture of Einstein, Bose was able to derive the radiation formula by systematically developing a statistics of mass-less particles without the constraint of particle number
conservation. Bose derived Planck's Law of Radiation by proposing different states for the photon. Instead of statistical independence of particles, Bose put particles into cells and described statistical independence of cells of phase space
. Such systems allow two polarization states, and exhibit totally symmetric wavefunctions.
He developed a statistical law governing the behavior pattern of photons quite successfully. However, he was not able to publish his work; no journals in Europe
would accept his paper, being unable to understand it. Bose sent his paper to Einstein, who saw the significance of it and used his influence to get it published.
 , each level
, each level
having energy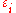 and containing a total of
and containing a total of
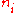 particles. Suppose each level contains
particles. Suppose each level contains

distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta, in which case they are distinguishable from each other, yet they can still have the same energy.
The value of
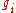 associated with level
associated with level 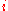 is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.
is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.
Let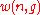 be the number of ways of distributing
be the number of ways of distributing
 particles among the
particles among the
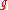 sublevels of an energy level. There is only one way of distributing
sublevels of an energy level. There is only one way of distributing
 particles with one sublevel, therefore
particles with one sublevel, therefore
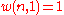 . It is easy to see that
. It is easy to see that
there are ways of distributing
ways of distributing
 particles in two sublevels which we will write as:
particles in two sublevels which we will write as:
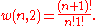
With a little thought
(see Notes below)
it can be seen that the number of ways of distributing
 particles in three sublevels is
particles in three sublevels is

so that
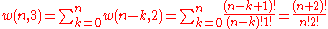
where we have used the following theorem involving binomial coefficient
s:
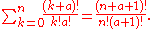
Continuing this process, we can see that
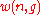
is just a binomial coefficient
(See Notes below)
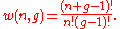
For example, the population numbers for two particles in three sublevels are 200, 110, 101, 020, 011, or 002 for a total of six which equals 4!/(2!2!). The number of ways that a set of occupation numbers can be realized is the product of the ways that each individual energy level can be populated:
can be realized is the product of the ways that each individual energy level can be populated:
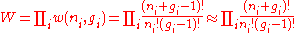
where the approximation assumes that . Following the same procedure used in deriving the Maxwell–Boltzmann statistics
. Following the same procedure used in deriving the Maxwell–Boltzmann statistics
, we wish to find the set of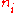 for which W is maximised, subject to the constraint that there be a fixed total number of particles, and a fixed total energy. The maxima of
for which W is maximised, subject to the constraint that there be a fixed total number of particles, and a fixed total energy. The maxima of  and
and 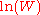 occur at the value of
occur at the value of 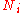 and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliers
and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliers
forming the function:

Using the approximation and using Stirling's approximation
approximation and using Stirling's approximation
for the factorials gives
gives
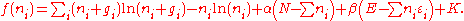
Where K is the sum of a number of terms which are not functions of the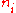 . Taking the derivative with respect to
. Taking the derivative with respect to 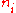 , and setting the result to zero and solving for
, and setting the result to zero and solving for 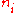 , yields the Bose–Einstein population numbers:
, yields the Bose–Einstein population numbers:
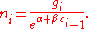
By a process similar to that outlined in the Maxwell-Boltzmann statistics article, it can be seen that: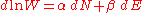
which, using Boltzmann's famous relationship becomes a statement of the second law of thermodynamics
becomes a statement of the second law of thermodynamics
at constant volume, and it follows that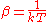 and
and 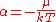 where S is the entropy
where S is the entropy
, is the chemical potential
is the chemical potential
, k is Boltzmann's constant and T is the temperature
, so that finally:
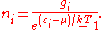
Note that the above formula is sometimes written:
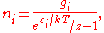
where
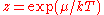
is the absolute activity
.
It is clear that the permutations of these n balls and g-1 partitions will give different ways of arranging bosons in different energy levels.
Say, for 3(=n) particles and 3(=g) shells, therefore (g-1)=2, the arrangement may be like
|..|. or
||... or
|.|..
etc.
Hence the number of distinct permutations of n + (g-1) objects which have n identical items and (g-1) identical items will be:
(n+g-1)!/n!(g-1)!
OR
The purpose of these notes is to clarify some aspects of the derivation of the Bose–Einstein (B–E)
distribution for beginners. The enumeration of cases (or ways) in the B–E distribution can be recast as
follows. Consider a game of dice throwing in which there are
 dice,
dice,
with each die taking values in the set
 , for
, for  .
.
The constraints of the game are that the value of a die
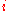 , denoted by
, denoted by  , has to be
, has to be
greater than or equal to the value of die
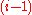 , denoted by
, denoted by
 , in the previous throw, i.e.,
, in the previous throw, i.e.,
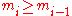 . Thus a valid sequence of die throws can be described by an
. Thus a valid sequence of die throws can be described by an
n-tuple
 , such that
, such that 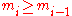 . Let
. Let
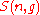 denote the set of these valid n-tuples:
denote the set of these valid n-tuples:
Then the quantity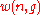 (defined above as the number of ways to distribute
(defined above as the number of ways to distribute
 particles among the
particles among the
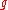 sublevels of an energy level) is the cardinality of
sublevels of an energy level) is the cardinality of 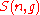 , i.e., the number of elements (or valid n-tuples) in
, i.e., the number of elements (or valid n-tuples) in 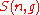 .
.
Thus the problem of finding an expression for
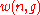
becomes the problem of counting the elements in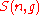 .
.
Example n = 4, g = 3:
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, Bose
Satyendra Nath Bose
Satyendra Nath Bose FRS was an Indian mathematician and physicist noted for his collaboration with Albert Einstein in developing a theory regarding the gaslike qualities of electromagnetic radiation. He is best known for his work on quantum mechanics in the early 1920s, providing the foundation...
–Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
statistics
Particle statistics
Particle statistics refers to the particular description of particles in statistical mechanics.-Classical statistics:In classical mechanics all the particles in the system are considered distinguishable. This means that one can label and track each individual particle in a system...
(or more colloquially B–E statistics) determines the statistical distribution of identical indistinguishable
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s over the energy states in thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
.
Concept
Fermi–Dirac and Bose–Einstein statistics apply when quantum effectsQuantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
are important and the particles are "indistinguishable
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
". Quantum effects appear if the concentration of particles satisfies N/V ≥ nq. Here nq is the quantum concentration
Quantum concentration
The quantum concentration nQ is the particle concentration of a system where the interparticle distance is equal to the thermal de Broglie wavelength or equivalently when the wavefunctions of the particles are touching but not overlapping.Quantum effects become appreciable when the particle...
, for which the interparticle distance is equal to the thermal de Broglie wavelength, so that the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s of the particles are touching but not overlapping. Fermi–Dirac statistics apply to fermions (particles that obey the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
), and Bose–Einstein statistics apply to bosons. As the quantum concentration depends on temperature; most systems at high temperatures obey the classical (Maxwell–Boltzmann) limit unless they have a very high density, as for a white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
. Both Fermi–Dirac and Bose–Einstein become Maxwell–Boltzmann statistics
Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
at high temperature or at low concentration.
Bosons, unlike fermions, are not subject to the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
: an unlimited number of particles may occupy the same state at the same time. This explains why, at low temperatures, bosons can behave very differently from fermions; all the particles will tend to congregate together at the same lowest-energy state, forming what is known as a Bose–Einstein condensate
Bose–Einstein condensate
A Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
.
B–E statistics was introduced for photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s in 1924 by Bose
Satyendra Nath Bose
Satyendra Nath Bose FRS was an Indian mathematician and physicist noted for his collaboration with Albert Einstein in developing a theory regarding the gaslike qualities of electromagnetic radiation. He is best known for his work on quantum mechanics in the early 1920s, providing the foundation...
and generalized to atoms by Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in 1924-25.
The expected number of particles in an energy state i for B–E statistics is
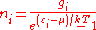
with εi > μ and where ni is the number of particles in state i, gi is the degeneracy
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
of state i, εi is the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the ith state, μ is the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
, k is the Boltzmann constant, and T is absolute temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
.
This reduces to the Rayleigh-Jeans distribution for
 , namely
, namely 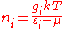 .
.History
In the early 1920s Satyendra Nath BoseSatyendra Nath Bose
Satyendra Nath Bose FRS was an Indian mathematician and physicist noted for his collaboration with Albert Einstein in developing a theory regarding the gaslike qualities of electromagnetic radiation. He is best known for his work on quantum mechanics in the early 1920s, providing the foundation...
, a Bengali
Bengali people
The Bengali people are an ethnic community native to the historic region of Bengal in South Asia. They speak Bengali , which is an Indo-Aryan language of the eastern Indian subcontinent, evolved from the Magadhi Prakrit and Sanskrit languages. In their native language, they are referred to as বাঙালী...
professor of University of Calcutta
University of Calcutta
The University of Calcutta is a public university located in the city of Kolkata , India, founded on 24 January 1857...
in British India was intrigued by Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of light waves being made of particles called photons. Bose was interested in mathematically deriving Planck's radiation formula, which Planck obtained largely by guessing. In 1900 Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
had derived his formula by manipulating the mathematics to fit the empirical evidence. Using the particle picture of Einstein, Bose was able to derive the radiation formula by systematically developing a statistics of mass-less particles without the constraint of particle number
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
conservation. Bose derived Planck's Law of Radiation by proposing different states for the photon. Instead of statistical independence of particles, Bose put particles into cells and described statistical independence of cells of phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. Such systems allow two polarization states, and exhibit totally symmetric wavefunctions.
He developed a statistical law governing the behavior pattern of photons quite successfully. However, he was not able to publish his work; no journals in Europe
Europe
Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...
would accept his paper, being unable to understand it. Bose sent his paper to Einstein, who saw the significance of it and used his influence to get it published.
A derivation of the Bose–Einstein distribution
Suppose we have a number of energy levels, labeled by index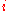 , each level
, each levelhaving energy
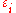 and containing a total of
and containing a total of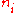 particles. Suppose each level contains
particles. Suppose each level contains
distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta, in which case they are distinguishable from each other, yet they can still have the same energy.
The value of
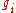 associated with level
associated with level 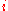 is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.
is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.Let
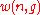 be the number of ways of distributing
be the number of ways of distributing particles among the
particles among the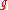 sublevels of an energy level. There is only one way of distributing
sublevels of an energy level. There is only one way of distributing particles with one sublevel, therefore
particles with one sublevel, therefore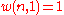 . It is easy to see that
. It is easy to see thatthere are
 ways of distributing
ways of distributing particles in two sublevels which we will write as:
particles in two sublevels which we will write as: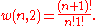
With a little thought
(see Notes below)
it can be seen that the number of ways of distributing
 particles in three sublevels is
particles in three sublevels is
so that
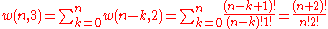
where we have used the following theorem involving binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s:
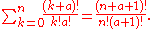
Continuing this process, we can see that
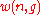
is just a binomial coefficient
(See Notes below)
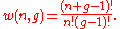
For example, the population numbers for two particles in three sublevels are 200, 110, 101, 020, 011, or 002 for a total of six which equals 4!/(2!2!). The number of ways that a set of occupation numbers
 can be realized is the product of the ways that each individual energy level can be populated:
can be realized is the product of the ways that each individual energy level can be populated: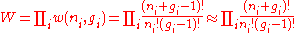
where the approximation assumes that
 . Following the same procedure used in deriving the Maxwell–Boltzmann statistics
. Following the same procedure used in deriving the Maxwell–Boltzmann statisticsMaxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
, we wish to find the set of
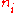 for which W is maximised, subject to the constraint that there be a fixed total number of particles, and a fixed total energy. The maxima of
for which W is maximised, subject to the constraint that there be a fixed total number of particles, and a fixed total energy. The maxima of  and
and 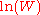 occur at the value of
occur at the value of 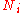 and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliers
and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliersLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
forming the function:

Using the
 approximation and using Stirling's approximation
approximation and using Stirling's approximationStirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
for the factorials
 gives
gives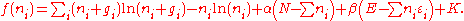
Where K is the sum of a number of terms which are not functions of the
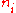 . Taking the derivative with respect to
. Taking the derivative with respect to 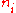 , and setting the result to zero and solving for
, and setting the result to zero and solving for 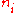 , yields the Bose–Einstein population numbers:
, yields the Bose–Einstein population numbers: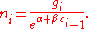
By a process similar to that outlined in the Maxwell-Boltzmann statistics article, it can be seen that:
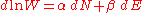
which, using Boltzmann's famous relationship
 becomes a statement of the second law of thermodynamics
becomes a statement of the second law of thermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
at constant volume, and it follows that
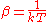 and
and 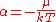 where S is the entropy
where S is the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
,
 is the chemical potential
is the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
, k is Boltzmann's constant and T is the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, so that finally:
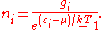
Note that the above formula is sometimes written:
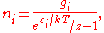
where
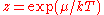
is the absolute activity
Activity
Activity may mean:* Action , in general* The Aristotelian concept of energeia, Latinized as actus* Physical exercise* Activity , a major task in Unified Modeling Language...
.
Notes
A much simpler way to think of Bose–Einstein distribution function is to consider that n particles are denoted by identical balls and g shells are marked by g-1 line partitions.It is clear that the permutations of these n balls and g-1 partitions will give different ways of arranging bosons in different energy levels.
Say, for 3(=n) particles and 3(=g) shells, therefore (g-1)=2, the arrangement may be like
|..|. or
||... or
|.|..
etc.
Hence the number of distinct permutations of n + (g-1) objects which have n identical items and (g-1) identical items will be:
(n+g-1)!/n!(g-1)!
OR
The purpose of these notes is to clarify some aspects of the derivation of the Bose–Einstein (B–E)
distribution for beginners. The enumeration of cases (or ways) in the B–E distribution can be recast as
follows. Consider a game of dice throwing in which there are
 dice,
dice,with each die taking values in the set
 , for
, for  .
.The constraints of the game are that the value of a die
 , denoted by
, denoted by  , has to be
, has to begreater than or equal to the value of die
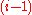 , denoted by
, denoted by , in the previous throw, i.e.,
, in the previous throw, i.e.,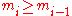 . Thus a valid sequence of die throws can be described by an
. Thus a valid sequence of die throws can be described by ann-tuple
 , such that
, such that 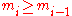 . Let
. Let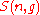 denote the set of these valid n-tuples:
denote the set of these valid n-tuples: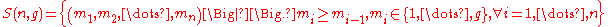 |
(1) |
Then the quantity
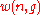 (defined above as the number of ways to distribute
(defined above as the number of ways to distribute particles among the
particles among the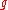 sublevels of an energy level) is the cardinality of
sublevels of an energy level) is the cardinality of 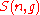 , i.e., the number of elements (or valid n-tuples) in
, i.e., the number of elements (or valid n-tuples) in 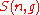 .
.Thus the problem of finding an expression for
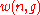
becomes the problem of counting the elements in
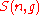 .
.Example n = 4, g = 3:

-
-
-
-
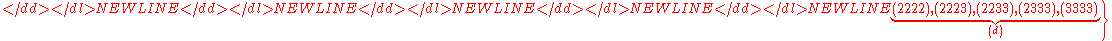
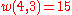 (there are
(there are  elements in
elements in 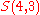 )
)
Subset

is obtained by fixing all indices
 to
to
 , except for the last index,
, except for the last index,
 , which is incremented from
, which is incremented from
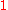 to
to
 .
.
Subset
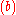
is obtained by fixing
 , and incrementing
, and incrementing
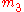 from
from
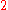 to
to
 . Due to the constraint
. Due to the constraint
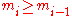
on the indices in
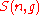 ,
,
the index
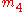 must
must
automatically
take values in
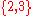 .
.
The construction of subsets
 and
and
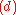
follows in the same manner.
Each element of
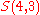 can be thought of as a
can be thought of as a
multisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of cardinality
 ;
;
the elements of such multiset are taken from the set
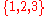
of cardinality
 ,
,
and the number of such multisets is the
multiset coefficient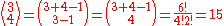
- Why "{3 + 4 - 1 \choose 3-1}"="{3 + 4 - 1 \choose 4}"? I Think you should write "\choose 3+1" instead of "\choose 3-1"
More generally, each element of

is a
multisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of cardinality

(number of dice)
with elements taken from the set

of cardinality
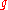
(number of possible values of each die),
and the number of such multisets, i.e.,
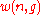
is the
multiset coefficient

(2)
which is exactly the same as the
formula for , as derived above with the aid
, as derived above with the aid
of
a theorem involving binomial coefficients, namely
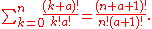
(3)
To understand the decomposition
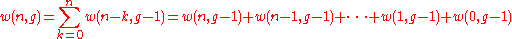
(4)
or for example,

and


let us rearrange the elements of
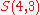 as follows
as follows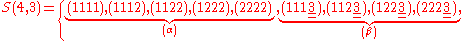
-
-
-
-
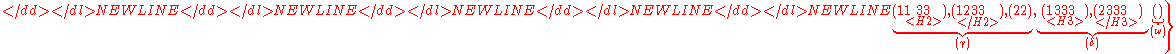 .
.
Clearly, the subset

of

is the same as the set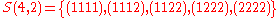 .
.
By deleting the index
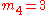
(shown in red with double underline)
in
the subset

of
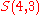 ,
,
one obtains
the set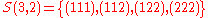 .
.
In other words, there is a one-to-one correspondence between the subset

of
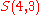
and the set
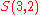 . We write
. We write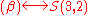 .
.
Similarly, it is easy to see that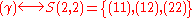
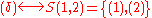
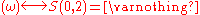 (empty set).
(empty set).
Thus we can write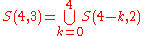
or more generally,
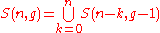 ;
;(5)
and since the sets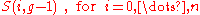
are non-intersecting, we thus have
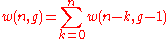 ,
,(6)
with the convention that .
.(7)
Continuing the process, we arrive at the following formula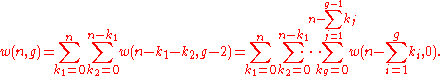
Using the convention (7)2 above, we obtain the formula
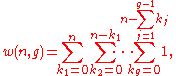
(8)
keeping in mind that for
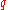
and
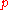
being constants, we have
 .
.(9)
It can then be verified that (8) and (2) give the same result for
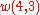 ,
,
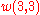 ,
,
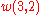 , etc.
, etc.
Interdisciplinary applications
Viewed as a pure probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, the Bose-Einstein distribution has found application in other fields:
- In recent years, Bose Einstein statistics have also been used as a method for term weighting in information retrievalInformation retrievalInformation retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
. The method is one of a collection of DFR ("Divergence From Randomness") models, the basic notion being that Bose Einstein statistics may be a useful indicator in cases where a particular term and a particular document have a significant relationship that would not have occurred purely by chance. Source code for implementing this model is available from the Terrier project at the University of Glasgow.
The evolution of many complex systems, including the World Wide Web, business, and citation networks, is encoded in the dynamic web describing the interactions between the system’s constituents. Despite their irreversible and nonequilibrium nature these networks follow Bose statistics and can undergo Bose–Einstein condensation. Addressing the dynamical properties of these nonequilibrium systems within the framework of equilibrium quantum gases predicts that the “first-mover-advantage,” “fit-get-rich(FGR),” and “winner-takes-all” phenomena observed in competitive systems are thermodynamically distinct phases of the underlying evolving networks .
See also- Bose–Einstein correlations
- BosonBosonIn particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
- Higgs bosonHiggs bosonThe Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
- Maxwell–Boltzmann statisticsMaxwell–Boltzmann statisticsIn statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
- Fermi–Dirac statistics
- ParastatisticsParastatisticsIn quantum mechanics and statistical mechanics, parastatistics is one of several alternatives to the better known particle statistics models...
- Planck's law of black body radiationPlanck's law of black body radiationIn physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
- In recent years, Bose Einstein statistics have also been used as a method for term weighting in information retrieval
-
-
-
-
-
-

