Angle trisection
Encyclopedia
Angle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics
. It concerns construction of an angle
equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge
, and a compass
.
With such tools, the task of angle trisection is generally impossible
, as shown by Pierre Wantzel
(1837). Wantzel's proof relies on ideas from the field of Galois theory
—in particular, trisection of an angle corresponds to the solution of a certain cubic equation, which is not possible using the given tool
s. Note that the fact that there is no way to trisect an angle in general with just a compass and a straightedge does not mean that it is impossible to trisect all angles: for example, it is relatively straightforward to trisect a right angle
(that is, to construct an angle of measure 30 degrees).
It is, however, possible to trisect an arbitrary angle, but using tools other than straightedge and compass. For example, neusis construction
, also known to ancient Greeks, involves simultaneous sliding and rotation of a marked straightedge, which can not be achieved with the original tools. Other techniques were developed by mathematicians over centuries.
Because it is defined in simple terms, but complex to prove unsolvable, the problem of angle trisection is a frequent subject of pseudomathematical
attempts at solution by naive enthusiasts. The "solutions" often involve finding loopholes in the rules, or are just plain wrong.
Using only an unmarked straightedge
and a compass
, Greek mathematicians
found means to divide a line
into an arbitrary set of equal segments, to draw parallel
lines, to bisect angles, to construct many polygon
s, and to construct square
s of equal or twice the area of a given polygon.
Three problems proved elusive, specifically, trisecting the angle, doubling the cube
, and squaring the circle
. The problem of angle trisection reads:
Construct an angle
equal to one-third of a given arbitrary angle, using only two tools:
The geometric problem of angle trisection can be related to algebra—specifically, to the problem of finding the roots of a cubic polynomial—since by the triple-angle formula, 
.
One can show that any number constructible
in one step from a field
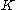is a solution of a second-order polynomial
. Note also that
radian
s (60 degree
s, written 60°) is constructible. We now show that it is impossible to construct a 20° angle; this implies that a 60° angle cannot be trisected, and thus that an arbitrary angle cannot be trisected.
Denote the set of rational numbers by Q. If 60° could be trisected, the minimal polynomial of over by Q would be of second order. Now let .
Note that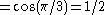
. Then by the triple-angle formula, 
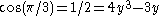and so 
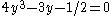. Thus 
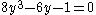, or equivalently 
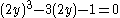. Now substitute 
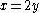, so that 
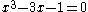. Let 
.
The minimal polynomial
for x (hence ) is a factor of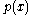
. Because 
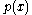is degree 3, if it is reducible over by Q then it has a rational root. By the rational root theorem, this root must be 1 or −1, but both are clearly not roots. Therefore 
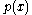is irreducible
over by Q, and the minimal polynomial for is of degree 3.
So an angle of 60° = (1/3)π radians cannot be trisected.
Many people (who presumably are unaware of the above result, misunderstand it, or incorrectly reject it) have proposed methods of trisecting the general angle. Some of these methods provide reasonable approximations; others (some of which are mentioned below) involve tools not permitted in the classical problem. The mathematician Underwood Dudley
has detailed some of these failed attempts in his book The Trisectors.
angle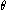
, the angle 
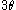can be trivially trisected by ignoring the given angle and directly constructing an angle of measure 
. There are also angles which, while non-constructible, are trisectible when given. For example, 
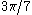is such an angle: five copies of 
combine to make an angle of measure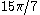 
, which is a full circle plus the necessary 
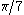. More generally, for a positive integer 
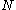, an angle of measure 
is trisectible if and only if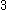 
does not divide 
.
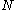Theorem
: The angle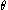
may be trisected if and only if
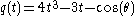is reducible over the field extension
Q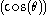
.
The proof
is a relatively straightforward generalization of the proof given above that a 60-degree angle is not trisectible.
. Huzita's axioms (types of folding operations) can construct cubic extensions (cube roots) of given lengths, whereas ruler-and-compass can construct only quadratic extensions (square roots).
which, if drawn on the plane using other methods, can be used to trisect arbitrary angles.
Another means to trisect an arbitrary angle by a "small" step outside the Greek framework is via a ruler with two marks a set distance apart. The next construction is originally due to Archimedes
, called a Neusis construction
, i.e., that uses tools other than an un-marked straightedge.
This requires three facts from geometry (at right):
At the diagram at right, angle a (left of point B) is the subject of trisection. First, a point A is drawn at an angle's ray, one unit apart from B. A circle of radius
AB is drawn.
Then, the markedness of the ruler comes into play: it is "anchored" at point A, and slided and rotated until one mark is at point C, and one at point D, i.e., CD = AB. A radius BC is drawn as obvious. That is to say, line segments AB, BC, and CD all have equal length. (Segment AC is irrelevant.) Now, Triangles ABC and BCD are isosceles, thus (by Fact 3 above) each has two equal angles.
Hypothesis
: Given AD is a straight line, and AB, BC, and CD are all equal length,
Conclusion: angle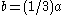
.
Proof
:
Clearing,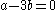
, or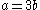 
, and the theorem
is proved
.
Again, this construction stepped outside the framework
of allowed constructions by using a marked straightedge. There is an unavoidable element of inaccuracy in placing the straightedge.
Hutcheson constructed a cylinder from the angle to be trisected by drawing an arc across the angle, completing it as a circle, and constructing from that circle a cylinder on which a, say, equilateral triangle was inscribed (a 360-degree angle divided in three). This was then "mapped" onto the angle to be trisected, with a simple proof of similar triangles.
A "tomahawk
" is a geometric shape consisting of a semicircle and two orthogonal line segments, such that the length of the shorter segment is equal to the circle radius. Trisection is executed by leaning the end of the tomahawk's shorter segment on one ray, the circle's edge on the other, so that the "handle" (longer segment) crosses the angle's vertex; the trisection line runs between the vertex and the center of the semicircle.
Note that while a tomahawk is constructible with compass and straightedge, it is not generally possible to construct a tomahawk in any desired position. Thus, the above construction does not contradict the nontrisectibility of angles with ruler and compass alone.
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
. It concerns construction of an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge
Straightedge
A straightedge is a tool with an edge free from curves, or straight, used for transcribing straight lines, or checking the straightness of lines...
, and a compass
Compass (drafting)
A compass or pair of compasses is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, they can also be used as a tool to measure distances, in particular on maps...
.
With such tools, the task of angle trisection is generally impossible
Proof of impossibility
A proof of impossibility, sometimes called a negative proof or negative result, is a proof demonstrating that a particular problem cannot be solved, or cannot be solved in general. Often proofs of impossibility have put to rest decades or centuries of work attempting to find a solution...
, as shown by Pierre Wantzel
Pierre Wantzel
Pierre Laurent Wantzel was a French mathematician who proved that several ancient geometric problems were impossible to solve using only compass and straightedge....
(1837). Wantzel's proof relies on ideas from the field of Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
—in particular, trisection of an angle corresponds to the solution of a certain cubic equation, which is not possible using the given tool
Tool
A tool is a device that can be used to produce an item or achieve a task, but that is not consumed in the process. Informally the word is also used to describe a procedure or process with a specific purpose. Tools that are used in particular fields or activities may have different designations such...
s. Note that the fact that there is no way to trisect an angle in general with just a compass and a straightedge does not mean that it is impossible to trisect all angles: for example, it is relatively straightforward to trisect a right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
(that is, to construct an angle of measure 30 degrees).
It is, however, possible to trisect an arbitrary angle, but using tools other than straightedge and compass. For example, neusis construction
Neusis construction
The neusis is a geometric construction method that was used in antiquity by Greek mathematicians.- Geometric construction :The neusis construction consists of fitting a line element of given length in between two given lines , in such a way that the line element, or its...
, also known to ancient Greeks, involves simultaneous sliding and rotation of a marked straightedge, which can not be achieved with the original tools. Other techniques were developed by mathematicians over centuries.
Because it is defined in simple terms, but complex to prove unsolvable, the problem of angle trisection is a frequent subject of pseudomathematical
Pseudomathematics
Pseudomathematics is a form of mathematics-like activity that does not work within the framework, definitions, rules, or rigor of formal mathematical models...
attempts at solution by naive enthusiasts. The "solutions" often involve finding loopholes in the rules, or are just plain wrong.
Background and problem statement
Straightedge
A straightedge is a tool with an edge free from curves, or straight, used for transcribing straight lines, or checking the straightness of lines...
and a compass
Compass (drafting)
A compass or pair of compasses is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, they can also be used as a tool to measure distances, in particular on maps...
, Greek mathematicians
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
found means to divide a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
into an arbitrary set of equal segments, to draw parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
lines, to bisect angles, to construct many polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s, and to construct square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s of equal or twice the area of a given polygon.
Three problems proved elusive, specifically, trisecting the angle, doubling the cube
Doubling the cube
Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
, and squaring the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
. The problem of angle trisection reads:
Construct an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
equal to one-third of a given arbitrary angle, using only two tools:
- An un-marked straightedgeStraightedgeA straightedge is a tool with an edge free from curves, or straight, used for transcribing straight lines, or checking the straightness of lines...
, and - a compassCompass (drafting)A compass or pair of compasses is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, they can also be used as a tool to measure distances, in particular on maps...
.
Proof of impossibility
.One can show that any number constructible
Constructible number
A point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
in one step from a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
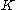is a solution of a second-order polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
. Note also that
radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s (60 degree
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
s, written 60°) is constructible. We now show that it is impossible to construct a 20° angle; this implies that a 60° angle cannot be trisected, and thus that an arbitrary angle cannot be trisected.
Denote the set of rational numbers by Q. If 60° could be trisected, the minimal polynomial of over by Q would be of second order. Now let .
Note that
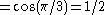. Then by the triple-angle formula, 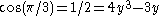and so 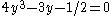. Thus 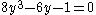, or equivalently 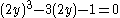. Now substitute 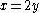, so tha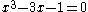t . Let .The minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
for x (hence ) is a factor of
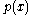. Because 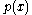is degree 3, if it is reducible over by Q then it has a rational root. By the rational root theorem, this root must be 1 or −1, but both are clearly not roots. Therefore 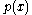is irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over by Q, and the minimal polynomial for is of degree 3.
So an angle of 60° = (1/3)π radians cannot be trisected.
Many people (who presumably are unaware of the above result, misunderstand it, or incorrectly reject it) have proposed methods of trisecting the general angle. Some of these methods provide reasonable approximations; others (some of which are mentioned below) involve tools not permitted in the classical problem. The mathematician Underwood Dudley
Underwood Dudley
Underwood Dudley is a mathematician, formerly of DePauw University, who has written a number of research works and textbooks but is best known for his popular writing. Most notable are several books describing crank mathematics by people who think they have squared the circle or done other...
has detailed some of these failed attempts in his book The Trisectors.
Angles which can be trisected
However, some angles can be trisected. For example, for any constructibleConstructibility
In mathematics, there are several notions of constructibility. Each of the following is by definition constructible:* a point in the Euclidean plane that can be constructed with compass and straightedge...
angle
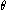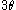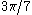, the angle can be trivially trisected by ignoring the given angle and directly constructing an angle of measure . There are also angles which, while non-constructible, are trisectible when given. For example, is such an angle: five copies of combine to make an angle of measure 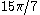, which is a full circle plus the necessary 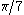. More generally, for a positive integer 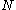, an angle of measure is trisectible if and only if 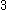does not divide 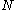.One general theorem
Again, denote the rational numbers Q:Theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
: The angle
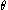may be trisected if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
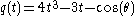is reducible over the field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
Q
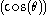.The proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
is a relatively straightforward generalization of the proof given above that a 60-degree angle is not trisectible.
Trisection using other methods
The general problem of angle trisection is solvable, but using additional tools, and thus going outside of the original Greek framework of compass and straightedge.By infinite repetition of bisection
Trisection can be achieved by infinite repetition of the compass and straightedge method and based on the binary representation of one-third (.010101...). The angle is bisected, then based on the binary fraction, a choice is made of what angle to bisect next. This algorithm is very similar to computer science's binary search and works for any fraction, even irrational ones.Using origami
Trisection, like many constructions impossible by ruler and compass, can easily be accomplished by the more powerful (but physically easy) operations of paper folding, or origamiOrigami
is the traditional Japanese art of paper folding, which started in the 17th century AD at the latest and was popularized outside Japan in the mid-1900s. It has since then evolved into a modern art form...
. Huzita's axioms (types of folding operations) can construct cubic extensions (cube roots) of given lengths, whereas ruler-and-compass can construct only quadratic extensions (square roots).
With an auxiliary curve
There are certain curves called trisectricesTrisectrix
In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of...
which, if drawn on the plane using other methods, can be used to trisect arbitrary angles.
With a marked ruler
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
, called a Neusis construction
Neusis construction
The neusis is a geometric construction method that was used in antiquity by Greek mathematicians.- Geometric construction :The neusis construction consists of fitting a line element of given length in between two given lines , in such a way that the line element, or its...
, i.e., that uses tools other than an un-marked straightedge.
This requires three facts from geometry (at right):
- Any full set of angles on a straight line add to 180°,
- The sum of angles of any triangle is 180°, and,
- Any two equal sides of an isosceles triangle will meet the third in the same anglePons asinorumPons asinorum is the name given to Euclid's fifth proposition in Book 1 of his Elements of geometry, also known as the theorem on isosceles triangles. It states that the angles opposite the equal sides of an isosceles triangle are equal...
.
At the diagram at right, angle a (left of point B) is the subject of trisection. First, a point A is drawn at an angle's ray, one unit apart from B. A circle of radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
AB is drawn.
Then, the markedness of the ruler comes into play: it is "anchored" at point A, and slided and rotated until one mark is at point C, and one at point D, i.e., CD = AB. A radius BC is drawn as obvious. That is to say, line segments AB, BC, and CD all have equal length. (Segment AC is irrelevant.) Now, Triangles ABC and BCD are isosceles, thus (by Fact 3 above) each has two equal angles.
Hypothesis
Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
: Given AD is a straight line, and AB, BC, and CD are all equal length,
Conclusion: angle
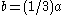.Proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
:
- From Fact 1) above,
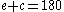°. - Looking at triangle BCD, from Fact 2)
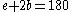°. - From the last two equations,
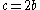. - From Fact 2),
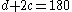°, thus 
°
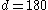, so from last,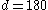 
°
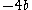. - From Fact 1) above,
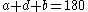°, thus 
°
°.
Clearing,
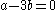, or 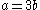, and the theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
is proved
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
.
Again, this construction stepped outside the framework
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
of allowed constructions by using a marked straightedge. There is an unavoidable element of inaccuracy in placing the straightedge.
With a string
Thomas Hutcheson published an article in the Mathematics Teacher that used a string instead of a compass and straight edge. A string can be used as either a straight edge (by stretching it) or a compass (by fixing one point and identifying another), but can also wrap around a cylinder, the key to Hutcheson's solution.Hutcheson constructed a cylinder from the angle to be trisected by drawing an arc across the angle, completing it as a circle, and constructing from that circle a cylinder on which a, say, equilateral triangle was inscribed (a 360-degree angle divided in three). This was then "mapped" onto the angle to be trisected, with a simple proof of similar triangles.
With a "tomahawk"
Tomahawk (geometric shape)
The tomahawk is a "tool" in geometry consisting of a semicircle and two line segments. The basic shape is constructible with compass and straightedge. It is possible to trisect an angle with the tomahawk...
" is a geometric shape consisting of a semicircle and two orthogonal line segments, such that the length of the shorter segment is equal to the circle radius. Trisection is executed by leaning the end of the tomahawk's shorter segment on one ray, the circle's edge on the other, so that the "handle" (longer segment) crosses the angle's vertex; the trisection line runs between the vertex and the center of the semicircle.
Note that while a tomahawk is constructible with compass and straightedge, it is not generally possible to construct a tomahawk in any desired position. Thus, the above construction does not contradict the nontrisectibility of angles with ruler and compass alone.
See also
- BisectionBisectionIn geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector In geometry, bisection is the division of something into two equal...
- Constructible numberConstructible numberA point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
- Constructible polygonConstructible polygonIn mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....
- Euclidean geometryEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
- History of geometry
- Intercept theoremIntercept theoremThe intercept theorem, also known as Thales' theorem , is an important theorem in elementary geometry about the ratios of various line segments that are created if two intersecting lines are intercepted by a pair of parallels. It is equivalent to the theorem about ratios in similar triangles...
- List of geometry topics
- Morley's trisector theoremMorley's trisector theoremIn plane geometry, Morley's trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the Morley triangle. The theorem was discovered in 1899 by Anglo-American mathematician Frank Morley...
- QuadratrixQuadratrixIn mathematics, a quadratrix is a curve having ordinates which are a measure of the area of another curve. The two most famous curves of this class are those of Dinostratus and E. W...
- TrisectrixTrisectrixIn geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of...
Additional references
- Courant, Richard, Herbert Robbins, Ian Stewart, What is mathematics?: an elementary approach to ideas and methods, Oxford University Press US, 1996. ISBN 9780195105193.
- Raghavendran, K. "Tripedal dividers of angles", Proceedings of Third International Measurement Conference (IMEKOIII), Stockholm, Sept. 1964.
External links
- MathWorld site
- Geometric problems of antiquity, including angle trisection
- Some history
- One link of marked ruler construction
- Another, mentioning Archimedes
- A long article with many approximations & means going outside the Greek framework
- Geometry site
Other means of trisection
- Trisecting via (Archived 2009-10-25) the limaconLimaçonIn geometry, a limaçon or limacon , also known as a limaçon of Pascal, is defined as a roulette formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller...
of PascalBlaise PascalBlaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
; see also TrisectrixTrisectrixIn geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of... - Trisecting via an Archimedean SpiralArchimedean spiralThe Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
- Trisecting via the ConchoidConchoid (mathematics)A conchoid is a curve derived from a fixed point O, another curve, and a length d. For every line through O that intersects the given curve at A the two points on the line which are d from A are on the conchoid. The conchoid is, therefore, the cissoid of a circle with center O and the given curve...
of NicomedesNicomedes (mathematician)Nicomedes was an ancient Greek mathematician.- Life and work :Almost nothing is known about his life apart from references in his works. We know that he lived around the time of Eratosthenes or after, because he criticized Eratosthenes' method of doubling the cube... - sciencenews.org site on using origamiOrigamiis the traditional Japanese art of paper folding, which started in the 17th century AD at the latest and was popularized outside Japan in the mid-1900s. It has since then evolved into a modern art form...
- Hyperbolic trisection and the spectrum of regular polygons