
Constructible number
Encyclopedia
A point
in the Euclidean plane is a constructible point if, given a fixed coordinate system
(or a fixed line segment
of unit length
), the point can be constructed with unruled straightedge and compass. A complex number
is a constructible number if its corresponding point in the Euclidean plane is constructible from the usual x- and y-coordinate axes.
It can then be shown that a real number
r is constructible if and only if
, given a line segment of unit length, a line segment of length |r | can be constructed with compass and straightedge. It can also be shown that a complex number is constructible if and only if its real and imaginary parts are constructible.
The set of constructible numbers can be completely characterized
in the language of field theory: the constructible numbers form the smallest field extension
of the rational number
s which is closed under square root
and complex conjugation
. This has the effect of transforming geometric questions about compass and straightedge constructions into algebra
. This transformation leads to the solutions of many famous mathematical problems, which defied centuries of attack.
Since the order of E, F, G, and H in the above definition is irrelevant, the four letters may be permuted
in any way. Put simply, Z is constructible from E, F, G and H if it lies in the intersection of any two distinct lines, or of any two distinct circles, or of a line and a circle, where these lines and/or circles can be determined by E, F, G, and H, in the above sense.
Now, let A and A′ be any two distinct fixed points in the plane. A point Z is constructible if either
Put simply, Z is constructible if it is either A or A′, or if it is obtainable from a finite sequence of points starting with A and A′, where each new point is constructible from previous points in the sequence.
For example, the center point of A and A′ is defined as follows. The circles C (A, A′) and C (A′, A) intersect in two distinct points; these points determine a unique line, and the center is defined to be the intersection of this line with L(A, A′).
s are constructible, and all constructible numbers are algebraic number
s. Also, if a and b are constructible numbers with b ≠ 0, then and a/b are constructible. Thus, the set K of all constructible complex numbers forms a field, a subfield of the field of algebraic numbers.
Furthermore, K is closed under square roots and complex conjugation. These facts can be used to characterize the field of constructible numbers, because, in essence, the equations defining lines and circles are no worse than quadratic. The characterization is the following: a complex number is constructible if and only if
it lies in a field at the top of a finite tower of quadratic extensions, starting with the rational field Q. More precisely, z is constructible if and only if there exists a tower of fields
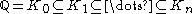
where z is in Kn and for all 0 ≤ j < n, the dimension [Kj + 1 : Kj ] = 2.
The non-constructibility of certain numbers proves the impossibility of certain problems attempted by the philosophers of ancient Greece
. In the following chart, each row represents a specific ancient construction problem. The left column gives the name of the problem. The second column gives an equivalent algebraic formulation of the problem. In other words, the solution to the problem is affirmative if and only if
each number in the given set of numbers is constructible. Finally, the last column provides the simplest known counterexample
. In other words, the number in the last column is an element of the set in the same row, but is not constructible.
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in the Euclidean plane is a constructible point if, given a fixed coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
(or a fixed line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
of unit length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
), the point can be constructed with unruled straightedge and compass. A complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
is a constructible number if its corresponding point in the Euclidean plane is constructible from the usual x- and y-coordinate axes.
It can then be shown that a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
r is constructible if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
, given a line segment of unit length, a line segment of length |r | can be constructed with compass and straightedge. It can also be shown that a complex number is constructible if and only if its real and imaginary parts are constructible.
The set of constructible numbers can be completely characterized
Characterization (mathematics)
In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
in the language of field theory: the constructible numbers form the smallest field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s which is closed under square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
and complex conjugation
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
. This has the effect of transforming geometric questions about compass and straightedge constructions into algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. This transformation leads to the solutions of many famous mathematical problems, which defied centuries of attack.
Geometric definitions
The geometric definition of a constructible point is as follows. First, for any two distinct points P and Q in the plane, let L(P, Q ) denote the unique line through P and Q, and let C (P, Q ) denote the unique circle with center P, passing through Q. (Note that the order of P and Q matters for the circle.) By convention, L(P, P ) = C (P, P ) = {P }. Then a point Z is constructible from E, F, G and H if either- Z is in the intersectionLine-line intersectionIn Euclidean geometry, the intersection of a line and a line can be the empty set,a point, ora line. Distinguishing these cases, and finding the intersection point have use, for example, in computer graphics, motion planning, and collision detection....
of L(E, F ) and L(G, H ), where L(E, F ) ≠ L(G, H ); - Z is in the intersection of C (E, F ) and C (G, H ), where C (E, F ) ≠ C (G, H );
- Z is in the intersection of L(E, F ) and C (G, H ).
Since the order of E, F, G, and H in the above definition is irrelevant, the four letters may be permuted
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
in any way. Put simply, Z is constructible from E, F, G and H if it lies in the intersection of any two distinct lines, or of any two distinct circles, or of a line and a circle, where these lines and/or circles can be determined by E, F, G, and H, in the above sense.
Now, let A and A′ be any two distinct fixed points in the plane. A point Z is constructible if either
- Z = A;
- Z = A′;
- there exist points P1, ..., Pn, with Z = Pn, such that for all j ≥ 1, Pj + 1 is constructible from points in the set {A, A′, P1, ..., Pj }.
Put simply, Z is constructible if it is either A or A′, or if it is obtainable from a finite sequence of points starting with A and A′, where each new point is constructible from previous points in the sequence.
For example, the center point of A and A′ is defined as follows. The circles C (A, A′) and C (A′, A) intersect in two distinct points; these points determine a unique line, and the center is defined to be the intersection of this line with L(A, A′).
Transformation into algebra
All rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s are constructible, and all constructible numbers are algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s. Also, if a and b are constructible numbers with b ≠ 0, then and a/b are constructible. Thus, the set K of all constructible complex numbers forms a field, a subfield of the field of algebraic numbers.
Furthermore, K is closed under square roots and complex conjugation. These facts can be used to characterize the field of constructible numbers, because, in essence, the equations defining lines and circles are no worse than quadratic. The characterization is the following: a complex number is constructible if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it lies in a field at the top of a finite tower of quadratic extensions, starting with the rational field Q. More precisely, z is constructible if and only if there exists a tower of fields
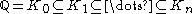
where z is in Kn and for all 0 ≤ j < n, the dimension [Kj + 1 : Kj ] = 2.
Impossible constructions
The algebraic characterization of constructible numbers provides an important necessary condition for constructibility: if z is constructible, then it is algebraic, and its minimal irreducible polynomial has degree a power of 2, or equivalently, the field extension Q(z)/Q has dimension a power of 2. One should note that it is true, (but not obvious to show) that the converse is false — this is not a sufficient condition for constructibility. However, this defect can be remedied by considering the normal closure of Q(z)/Q.The non-constructibility of certain numbers proves the impossibility of certain problems attempted by the philosophers of ancient Greece
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
. In the following chart, each row represents a specific ancient construction problem. The left column gives the name of the problem. The second column gives an equivalent algebraic formulation of the problem. In other words, the solution to the problem is affirmative if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
each number in the given set of numbers is constructible. Finally, the last column provides the simplest known counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
. In other words, the number in the last column is an element of the set in the same row, but is not constructible.
| Construction problem | Associated set of numbers | Counterexample |
|---|---|---|
| Doubling the cube Doubling the cube Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction... |
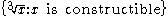 |
 is not constructible, because its minimal polynomial is not constructible, because its minimal polynomialMinimal polynomial (field theory) In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0... has degree 3 over Q |
| Trisecting the angle |  |
 is not constructible, because is not constructible, because  has minimal polynomial of degree 3 over Q has minimal polynomial of degree 3 over Q |
| Squaring the circle Squaring the circle Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge... |
 |
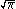 is not constructible, because it is not algebraic over Q is not constructible, because it is not algebraic over Q |
| Constructing all regular polygons Constructible polygon In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not.... |
 |
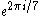 is not constructible, because 7 is not a Fermat prime, nor is 7 the product of 2^k and one or more Fermat primes is not constructible, because 7 is not a Fermat prime, nor is 7 the product of 2^k and one or more Fermat primes |
See also
- Computable numberComputable numberIn mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
- Definable real number
- Compass and straightedge constructions

