
Wigner-Eckart theorem
Encyclopedia
The Wigner–Eckart theorem is a theorem
of representation theory
and quantum mechanics
. It states that matrix
elements of spherical tensor operator
s on the basis of angular momentum
eigenstates can be expressed as the product of two factors, one of which is independent of angular momentum orientation, and the other a Clebsch-Gordan coefficient. The name derives from physicists Eugene Wigner and Carl Eckart
who developed the formalism as a link between the symmetry transformation groups of space (applied to the Schrödinger equations) and the laws of conservation of energy, momentum, and angular momentum.
The Wigner-Eckart theorem reads:
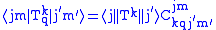
where is a rank
is a rank 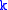 spherical tensor,
spherical tensor,  and
and 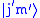 are eigenkets of total angular momentum
are eigenkets of total angular momentum 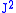 and its z-component
and its z-component 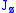 ,
,  has a value which is independent of
has a value which is independent of  and
and  , and
, and 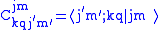 is the Clebsch-Gordan coefficient for adding
is the Clebsch-Gordan coefficient for adding 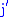 and
and 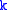 to get
to get  .
.
In effect, the Wigner–Eckart theorem says that operating with a spherical tensor operator of rank on an angular momentum eigenstate is like adding a state with angular momentum
on an angular momentum eigenstate is like adding a state with angular momentum 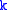 to the state. The matrix element one finds for the spherical tensor operator is proportional to a Clebsch-Gordan coefficient, which arises when considering adding two angular momenta.
to the state. The matrix element one finds for the spherical tensor operator is proportional to a Clebsch-Gordan coefficient, which arises when considering adding two angular momenta.
 . This matrix element is the expectation value of a Cartesian operator in a spherically-symmetric hydrogen-atom-eigenstate basis
. This matrix element is the expectation value of a Cartesian operator in a spherically-symmetric hydrogen-atom-eigenstate basis
, which is a nontrivial problem. However, using the Wigner–Eckart theorem simplifies the problem. (In fact, we could get the solution right away using parity
, but we'll go a slightly longer way.)
We know that is one component of
is one component of  , which is a vector. Vectors are rank-1 tensors, so
, which is a vector. Vectors are rank-1 tensors, so  is some linear combination of
is some linear combination of  for
for  . In fact, it can be shown that
. In fact, it can be shown that 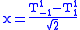 , where we defined the
, where we defined the
spherical tensors
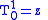
and
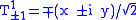 (the pre-factors have to be chosen according to the definition of a spherical tensor of rank
(the pre-factors have to be chosen according to the definition of a spherical tensor of rank  . Hence, the
. Hence, the  are only proportional to the ladder operators).
are only proportional to the ladder operators).
Therefore
The above expression gives us the matrix element for in the
in the  basis. To find the expectation value, we set
basis. To find the expectation value, we set 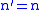 ,
,  , and
, and 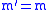 . The selection rule for
. The selection rule for  and
and  is
is  for the
for the 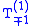 spherical tensors. As we have
spherical tensors. As we have 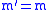 , this makes the Clebsch-Gordan Coefficients zero, leading to the expectation value to be equal to zero.
, this makes the Clebsch-Gordan Coefficients zero, leading to the expectation value to be equal to zero.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
of representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. It states that matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
elements of spherical tensor operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
s on the basis of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
eigenstates can be expressed as the product of two factors, one of which is independent of angular momentum orientation, and the other a Clebsch-Gordan coefficient. The name derives from physicists Eugene Wigner and Carl Eckart
Carl Eckart
Carl Henry Eckart was an American physicist, physical oceanographer, geophysicist, and administrator. He co-developed the Wigner-Eckart theorem and is also known for the Eckart conditions in quantum mechanics.-Education:Eckart began college in 1919 at Washington University in St...
who developed the formalism as a link between the symmetry transformation groups of space (applied to the Schrödinger equations) and the laws of conservation of energy, momentum, and angular momentum.
The Wigner-Eckart theorem reads:
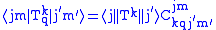
where
 is a rank
is a rank 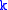 spherical tensor,
spherical tensor,  and
and 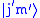 are eigenkets of total angular momentum
are eigenkets of total angular momentum 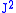 and its z-component
and its z-component 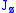 ,
,  has a value which is independent of
has a value which is independent of  and
and  , and
, and 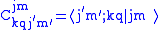 is the Clebsch-Gordan coefficient for adding
is the Clebsch-Gordan coefficient for adding 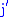 and
and 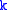 to get
to get  .
.In effect, the Wigner–Eckart theorem says that operating with a spherical tensor operator of rank
 on an angular momentum eigenstate is like adding a state with angular momentum
on an angular momentum eigenstate is like adding a state with angular momentum 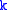 to the state. The matrix element one finds for the spherical tensor operator is proportional to a Clebsch-Gordan coefficient, which arises when considering adding two angular momenta.
to the state. The matrix element one finds for the spherical tensor operator is proportional to a Clebsch-Gordan coefficient, which arises when considering adding two angular momenta.Example
Consider the position expectation value . This matrix element is the expectation value of a Cartesian operator in a spherically-symmetric hydrogen-atom-eigenstate basis
. This matrix element is the expectation value of a Cartesian operator in a spherically-symmetric hydrogen-atom-eigenstate basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, which is a nontrivial problem. However, using the Wigner–Eckart theorem simplifies the problem. (In fact, we could get the solution right away using parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
, but we'll go a slightly longer way.)
We know that
 is one component of
is one component of  , which is a vector. Vectors are rank-1 tensors, so
, which is a vector. Vectors are rank-1 tensors, so  is some linear combination of
is some linear combination of  for
for  . In fact, it can be shown that
. In fact, it can be shown that 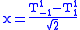 , where we defined the
, where we defined thespherical tensors
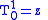
and
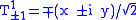 (the pre-factors have to be chosen according to the definition of a spherical tensor of rank
(the pre-factors have to be chosen according to the definition of a spherical tensor of rank  . Hence, the
. Hence, the  are only proportional to the ladder operators).
are only proportional to the ladder operators).Therefore

The above expression gives us the matrix element for
 in the
in the  basis. To find the expectation value, we set
basis. To find the expectation value, we set 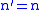 ,
,  , and
, and 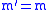 . The selection rule for
. The selection rule for  and
and  is
is  for the
for the 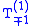 spherical tensors. As we have
spherical tensors. As we have 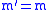 , this makes the Clebsch-Gordan Coefficients zero, leading to the expectation value to be equal to zero.
, this makes the Clebsch-Gordan Coefficients zero, leading to the expectation value to be equal to zero.External links
- J. J. Sakurai, (1994). "Modern Quantum Mechanics", Addison Wesley, ISBN 0-201-53929-2.
- Wigner–Eckart theorem
- Tensor Operators

