Weight (representation theory)
Encyclopedia
In the mathematical
field of representation theory
, a weight of an algebra
A over a field F is an algebra homomorphism
from A to F – a linear functional
– or equivalently, a one dimensional representation
of A over F. It is the algebra analogue of a multiplicative character of a group
. The importance of the concept, however, stems from its application to representations of Lie algebra
s and hence also to representations
of algebraic
and Lie group
s. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.
, each of which is diagonalizable
, and any two of which commute, it is always possible to simultaneously diagonalize all of the elements of S.The converse is also true – a set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalisable .In fact, given a set of commuting matrices over an algebraically closed field, they are simultaneously triangularizable, without needing to assume that they are diagonalizable. Equivalently, for any set S of mutually commuting semisimple linear transformation
s of a finite-dimensional vector space
V there exists a basis of V consisting of simultaneous eigenvectors of all elements of S. Each of these common eigenvectors v ∈ V, defines a linear functional
on the subalgebra U of End(V) generated by the set of endomorphisms S; this functional is defined as the map which associates to each element of U its eigenvalue on the eigenvector v. This "generalized eigenvalue" is a prototype for the notion of a weight.
The notion is closely related to the idea of a multiplicative character in group theory
, which is a homomorphism χ from a group
G to the multiplicative group
of a field
F. Thus χ: G → F× satisfies χ(e) = 1 (where e is the identity element
of G) and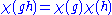
for all g, h in G.
Indeed, if G acts
on a vector space V over F, each simultaneous eigenspace for every element of G, if such exists, determines a multiplicative character on G; the eigenvalue on this common eigenspace of each element of the group.
The notion of multiplicative character can be extended to any algebra
A over F, by replacing χ: G → F× by a linear map χ: A → F with
for all a, b in A.
If an algebra A acts on a vector space V over F to any simultaneous eigenspace corresponds an algebra homomorphism
from A to F assigning to each element of A its eigenvalue.
If A is a Lie algebra
, then the commutativity of the field and the anticommutativity of the Lie bracket imply that this map vanish on commutator
s : χ([a,b])=0. A weight on a Lie algebra g over a field F is a linear map λ: g → F with λ([x,y])=0 for all x, y in g. Any weight on a Lie algebra g vanishes on the derived algebra [g,g] and hence descends to a weight on the abelian Lie algebra g/[g,g]. Thus weights are primarily of interest for abelian Lie algebras, where they reduce to the simple notion of a generalized eigenvalue for space of commuting linear transformations.
If G is a Lie group
or an algebraic group
, then a multiplicative character θ: G → F× induces a weight χ = dθ: g → F on its Lie algebra by differentiation. (For Lie groups, this is differentiation at the identity element of G, and the algebraic group case is an abstraction using the notion of a derivation.)
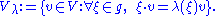
A weight of the representation V is a weight λ such that the corresponding weight space is nonzero. Nonzero elements of the weight space are called weight vectors.
If V is the direct sum of its weight spaces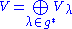
then it is called a ; this corresponds to having an eigenbasis (a basis of eigenvectors), i.e., being a diagonalizable matrix
.
Similarly, we can define a weight space Vλ for any representation
of a Lie group
or an associative algebra
.
, h a maximal
commutative Lie subalgebra consisting of semi-simple elements (sometimes called Cartan subalgebra) and let V be a finite dimensional representation of g. If g is semisimple, then [g,g] = g and so all weights on g are trivial. However, V is, by restriction, a representation of h, and it is well known that V is a weight module for h, i.e., equal to the direct sum of its weight spaces. By an abuse of language, the weights of V as a representation of h are often called weights of V as a representation of g.
Similar definitions apply to a Lie group G, a maximal commutative Lie subgroup
H and any representation V of G. Clearly, if λ is a weight of the representation V of G, it is also a weight of V as a representation of the Lie algebra g of G.
If V is the adjoint representation of g, its weights are called roots
, the weight spaces are called root spaces, and weight vectors are sometimes called root vectors.
We now assume that g is semisimple, with a chosen Cartan subalgebra h and corresponding root system
. Let us suppose also that a choice of positive roots
has been fixed. This is equivalent to the choice of a set of simple root
s.
be the real subspace of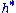 
(if it is complex) generated by the roots of 
.
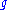There are two concepts how to define an ordering
of
.
The first one is
The second concept is given by an element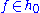
and
Usually, f is chosen so that β(f) > 0 for each positive root β.
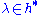is integral (or 
-integral), if 
for each coroot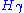 
such that 
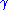is a positive root.
The fundamental weights
are defined by the property that they form a basis of 
dual to the set of simple coroots 
.
Hence λ is integral if it is an integral combination of the fundamental weights. The set of all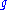
-integral weights is a lattice in 
called weight lattice for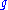 
, denoted by 
.
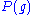A weight λ of the Lie group G is called integral, if for each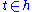
such that 
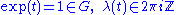. For G semisimple, the set of all G-integral weights is a sublattice 
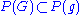. If G is simply connected, then 
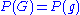. If G is not simply connected, then the lattice 
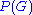is smaller than 
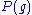and their quotient is isomorphic to the fundamental group
of G.
for each coroot 
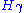such that γ is a positive root. Equivalently, λ is dominant, if it is a non-negative linear combination of the fundamental weights.
The convex hull
of the dominant weights is sometimes called the fundamental Weyl chamber.
Sometimes, the term dominant weight is used to denote a dominant (in the above sense) and integral weight.
Similarly, we define the lowest weight.
The space of all possible weights is a vector space. Let's fix a total ordering of this vector space such that a nonnegative linear combination
of positive vectors with at least one nonzero coefficient is another positive vector.
Then, a representation is said to have highest weight λ if λ is a weight and all its other weights are less than λ.
Similarly, it is said to have lowest weight λ if λ is a weight and all its other weights are greater than it.
A weight vector
of weight λ is called a highest-weight vector, or vector of highest weight, if all other weights of V are smaller than λ.
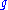is called highest-weight module if it is generated by a weight vector 
that is annihilated by the action of all positive root spaces in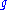 
.
This is something more special than a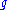
-module
with a highest weight.
Similarly we can define a highest-weight module for representation of a Lie group
or an associative algebra
.
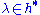, there exists a unique (up to isomorphism) simple highest-weight 
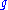-module with highest weight λ, which is denoted L(λ).
It can be shown that each highest weight module with highest weight λ is a quotient
of the Verma module
M(λ). This is just a restatement of universality property in the definition of a Verma module.
A highest-weight module is a weight module. The weight spaces in a highest-weight module are always finite dimensional.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, a weight of an algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
A over a field F is an algebra homomorphism
Algebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
from A to F – a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
– or equivalently, a one dimensional representation
Representation (mathematics)
In mathematics, representation is a very general relationship that expresses similarities between objects. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the...
of A over F. It is the algebra analogue of a multiplicative character of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. The importance of the concept, however, stems from its application to representations of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s and hence also to representations
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of algebraic
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
and Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.
Weights
Given a set S of matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, each of which is diagonalizable
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
, and any two of which commute, it is always possible to simultaneously diagonalize all of the elements of S.The converse is also true – a set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalisable .In fact, given a set of commuting matrices over an algebraically closed field, they are simultaneously triangularizable, without needing to assume that they are diagonalizable. Equivalently, for any set S of mutually commuting semisimple linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V there exists a basis of V consisting of simultaneous eigenvectors of all elements of S. Each of these common eigenvectors v ∈ V, defines a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on the subalgebra U of End(V) generated by the set of endomorphisms S; this functional is defined as the map which associates to each element of U its eigenvalue on the eigenvector v. This "generalized eigenvalue" is a prototype for the notion of a weight.
The notion is closely related to the idea of a multiplicative character in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, which is a homomorphism χ from a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G to the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F. Thus χ: G → F× satisfies χ(e) = 1 (where e is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of G) and
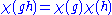for all g, h in G.Indeed, if G acts
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
on a vector space V over F, each simultaneous eigenspace for every element of G, if such exists, determines a multiplicative character on G; the eigenvalue on this common eigenspace of each element of the group.
The notion of multiplicative character can be extended to any algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
A over F, by replacing χ: G → F× by a linear map χ: A → F with
for all a, b in A.If an algebra A acts on a vector space V over F to any simultaneous eigenspace corresponds an algebra homomorphism
Algebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
from A to F assigning to each element of A its eigenvalue.
If A is a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, then the commutativity of the field and the anticommutativity of the Lie bracket imply that this map vanish on commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
s : χ([a,b])=0. A weight on a Lie algebra g over a field F is a linear map λ: g → F with λ([x,y])=0 for all x, y in g. Any weight on a Lie algebra g vanishes on the derived algebra [g,g] and hence descends to a weight on the abelian Lie algebra g/[g,g]. Thus weights are primarily of interest for abelian Lie algebras, where they reduce to the simple notion of a generalized eigenvalue for space of commuting linear transformations.
If G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
or an algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
, then a multiplicative character θ: G → F× induces a weight χ = dθ: g → F on its Lie algebra by differentiation. (For Lie groups, this is differentiation at the identity element of G, and the algebraic group case is an abstraction using the notion of a derivation.)
Weight space of a representation
Let V be a representation of a Lie algebra g over a field F and let λ be a weight of g. Then the weight space of V with weight λ: g → F is the subspace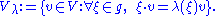A weight of the representation V is a weight λ such that the corresponding weight space is nonzero. Nonzero elements of the weight space are called weight vectors.
If V is the direct sum of its weight spaces
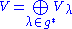
then it is called a ; this corresponds to having an eigenbasis (a basis of eigenvectors), i.e., being a diagonalizable matrix
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
.
Similarly, we can define a weight space Vλ for any representation
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
or an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
.
Semisimple Lie algebras
Let g be a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, h a maximal
Maximal
Maximal may refer to:*Maximal element, a mathematical definition*Maximal , a faction of Transformers*Maximalism, an artistic style*Maximal set*Maxim , a men's magazine marketed as Maximal in several countriesSee also...
commutative Lie subalgebra consisting of semi-simple elements (sometimes called Cartan subalgebra) and let V be a finite dimensional representation of g. If g is semisimple, then [g,g] = g and so all weights on g are trivial. However, V is, by restriction, a representation of h, and it is well known that V is a weight module for h, i.e., equal to the direct sum of its weight spaces. By an abuse of language, the weights of V as a representation of h are often called weights of V as a representation of g.
Similar definitions apply to a Lie group G, a maximal commutative Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
H and any representation V of G. Clearly, if λ is a weight of the representation V of G, it is also a weight of V as a representation of the Lie algebra g of G.
If V is the adjoint representation of g, its weights are called roots
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, the weight spaces are called root spaces, and weight vectors are sometimes called root vectors.
We now assume that g is semisimple, with a chosen Cartan subalgebra h and corresponding root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
. Let us suppose also that a choice of positive roots
has been fixed. This is equivalent to the choice of a set of simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s.
Ordering on the space of weights
Let be the real subspace of 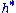(if it is complex) generated by the roots of 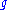.There are two concepts how to define an ordering
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
of
.The first one is
- μ ≤ λ if and only if λ − μ is nonnegative linear combination of simple rootSimple rootin mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s.
The second concept is given by an element
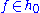and
- μ ≤ λ if and only if μ(f) ≤ λ(f).
Usually, f is chosen so that β(f) > 0 for each positive root β.
Integral weight
A weight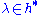 is integral (or -integral), if for each coroot 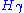such that 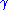is a positive root.The fundamental weights
are defined by the property that they form a basis of dual to the set of simple coroots .Hence λ is integral if it is an integral combination of the fundamental weights. The set of all
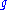-integral weights is a lattice in called weight lattice for 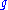, denoted by 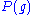.A weight λ of the Lie group G is called integral, if for each
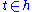such that 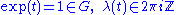. For G semisimple, the set of all G-integral weights is a sublattice 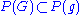. If G is simply connected, then 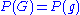. If G is not simply connected, then the lattice 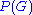is smaller than 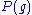and their quotient is isomorphic to the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of G.
Dominant weight
A weight λ is dominant, if for each coroot 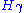such that γ is a positive root. Equivalently, λ is dominant, if it is a non-negative linear combination of the fundamental weights.The convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the dominant weights is sometimes called the fundamental Weyl chamber.
Sometimes, the term dominant weight is used to denote a dominant (in the above sense) and integral weight.
Highest weight
A weight λ of a representation V is called highest-weight, if no other weight of V is larger than λ. Sometimes, it is assumed that a highest weight is a weight, such that all other weights of V are strictly smaller than λ in the partial ordering given above. The term highest weight denotes often the highest weight of a "highest-weight module".Similarly, we define the lowest weight.
The space of all possible weights is a vector space. Let's fix a total ordering of this vector space such that a nonnegative linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of positive vectors with at least one nonzero coefficient is another positive vector.
Then, a representation is said to have highest weight λ if λ is a weight and all its other weights are less than λ.
Similarly, it is said to have lowest weight λ if λ is a weight and all its other weights are greater than it.
A weight vector
of weight λ is called a highest-weight vector, or vector of highest weight, if all other weights of V are smaller than λ.Highest-weight module
A representation V of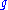 is called highest-weight module if it is generated by a weight vector that is annihilated by the action of all positive root spaces in 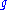.This is something more special than a
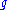-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
with a highest weight.
Similarly we can define a highest-weight module for representation of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
or an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
.
Verma module
For each weight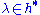, there exists a unique (up to isomorphism) simple highest-weight 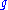-module with highest weight λ, which is denoted L(λ).It can be shown that each highest weight module with highest weight λ is a quotient
Quotient module
In abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
of the Verma module
Verma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
M(λ). This is just a restatement of universality property in the definition of a Verma module.
A highest-weight module is a weight module. The weight spaces in a highest-weight module are always finite dimensional.